圆锥曲线中三角形面积问题的简洁处理

☉江苏省滨海中学 乔井贵

圆锥曲线中三角形面积问题的简洁处理

☉江苏省滨海中学 乔井贵

圆锥曲线中涉及三角形面积最值的问题是高考常考题型，它能考查圆锥曲线的性质，重要公式的应用及解析几何中的设而不求思想，这与高考命题指导思想在知识交汇处命题相吻合.另一方面，面积最值问题的综合性、复杂性、思维性，能充分考查学生综合应用知识的能力.此类问题的求解关键在于面积公式的选择.下面以2012年北京高考题及模拟题为例说明.

（1）求椭圆M的方程；

（2）设直线l与椭圆M交于A、B两点，且以AB为直径的圆过椭圆的右顶点C，求△ABC面积的最大值.

（2）不妨设直线AB的方程为x=ky+m.

（1）求椭圆C的方程；

（2）过点P（0，2）的直线交椭圆C于A、B两点，求△AOB（O为原点）面积的最大值.

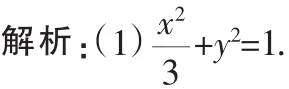
（2）易知直线AB的斜率存在，设其方程为y=kx+2.

将直线AB的方程与椭圆C的方程联立，消去y得（1+3k2）x2+12kx+9=0.

点评：由于OP=2，所以应当将△OAB拆分为△OPA、△OPB两个三角形求面积.以OP为底，分别以A、B到OP的距离为高，△OAB的面积的最简单的表示形式为：S△AOB=

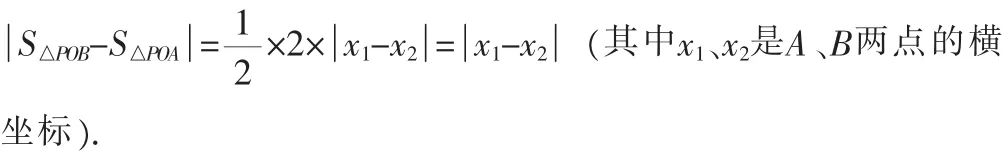
（1）求椭圆C的方程；