让学生成为灵动的“舞”者、智性的“悟”者——动感数学课堂初探

☉江苏省如皋中学 姚新国

让学生成为灵动的“舞”者、智性的“悟”者
——动感数学课堂初探

☉江苏省如皋中学 姚新国

在高中数学教学中，培养学生能力的核心是诱发学生的数学思维，而要培养学生的数学思维，就应该为学生搭建一个“动感”平台，让学生在主动活动的过程中自我调动各种感官，即动眼观察、动耳倾听、动手操作、动口交流、动脑思考，感悟学习过程中成功的喜悦，体验学习过程中数学思维的流畅性、知识生成的动态性、合作探究的愉悦性，在宽松、自由、开放的动态课堂中提升自身的数学素养．

怎样让数学课堂成为“动感地带”呢？笔者认为首先要落实好成为“动感地带”的三要素．

一、数学课堂成为“动感地带”的三要素

1．给学生动感的源泉

笔者发现很多数学课堂还是教师“自导自演”，学生参与度不高，缺乏参与的激情是其中一个不容忽视的重要原因，在教学中，创设紧扣教学内容和启迪学生思维的问题情境，无疑会使课堂充满情趣，有利于激发学生产生求知欲，激发学生“动”的热情．如推导等比数列求和公式时，可先让学生回忆等差数列求和公式的推导思路，学生发现首尾两项之间和的关系，将中间的项两两合并为首尾两项的和，目的是将中间所有项消去，那么等比数列求和公式能否通过某个技巧，也将部分中间的项消去，用简洁美观的公式表示呢？再如认识椭圆概念时，可进行实验演示，如有圆柱形的半杯水，观察杯子倾斜时水面的形状等.［1］

2.让学生成为灵动的“舞者”

高中学生已经有了一定的分析能力和是非判断能力，他们希望能与教师在互相尊重、信任的基础上，通过倾听、言谈、展示进行多向沟通.在我们的课堂上要减少灌输，多些沟通，让学生愿意去思考，学会思考，这样我们所希望的学生自己动手操作、实践探究、主动观察、试验、猜想、验证、得结论、将结论推广和应用的范式教学才能真正落到实处，成为我们的常态教学范式，从而保证课堂和谐流畅，让学生成为灵动的“舞者”.

3.让学生成为智性的“悟”者

在我们的课堂教学中，教师不仅要给学生知识、技能，更要给学生研究问题的方法和努力的方向，进一步能提出问题，这样的课堂教学常常让学生感觉有自己的发现，感觉有成就感，逐步建立自信心.要达到这个目标，则必须给学生时间和空间，在反思和感悟中让学生成为智性的“悟”者.

二、新授课中的“动感地带”

下面笔者结合新授课和习题课两个案例谈谈具体的操作过程.

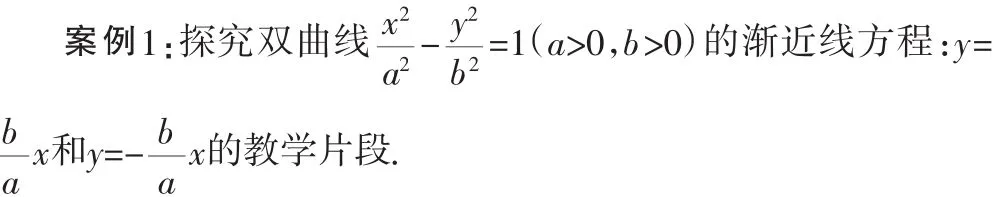
1.创设情境，激发学生“动”的热情

学生思考片刻.教师继续点拨，激发学生的探究欲望.

学生产生了探究的欲望，部分学生开始动笔作图，还有部分学生相互讨论、争辩，一个个忙得不亦乐乎.教师巡视发现有学生从特殊情况入手，通过画图去探求直线.

师：请某个小组展示本组的研究成果.

生：双曲线的图形在以直线为边界的平面区域内.

师：你是怎样得到的？

生：画图，从图形观察得来的.

生：根据对称性，可以先研究双曲线在第一象限的部分与直线y=x的关系.

师：请同学们交流展示你们的研究方法和结果.

生：猜想：直线与双曲线没有交点，都向右上方无限延伸，并且无限接近.

师：他的猜想正确吗？能给出证明吗？

教师在提问时，要让学生体会到如何提问，即告诉学生提问的角度和创设问题的方式方法和问题的表达方式.

探究到这里，学生研究问题的欲望非常迫切，非常想证实自己的猜想，这时给他们独立思考探究的时间，让他们真正有所得.

2.“感”的基石——交流探究

在我们的课堂教学中，要让学生真正有所得有所感悟，教师必须让学生参与到知识与技能的形成过程中来，体验过程，交流探究.在探究时教师要指明探究方向和探究方法.［2］

3.深化理解感悟提升

研究一个新问题，首先要确定研究的方法和思路.我们研究解析几何等问题的思路一般都是从形的方面直观感知，提出猜想，验证，修正猜想，再从数的方面进行逻辑论证.

师：请同学们结合刚才解决问题的过程总结一下自己有什么收获.你还能继续探求出与双曲线渐近线有关的结论吗？

感悟：（1）总结研究问题的方法.

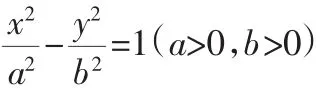
（3）在我们所研究的图像或曲线中，还有哪些图像或曲线也具有渐近线性质呢？

三、习题课中的“动感地带”

1．变式设问，产生“动”的火花

在课堂教学中，教师要放手让学生思考，寻找解题思路，通过变式设问，激起学生的探究欲望，增强学生的探究意识．让学生掌握变式的思路、规律和方向，逐渐让学生学会自己变式，自己提出有价值的问题来研究．

师：请大家独立思考．

学生通过设点P的坐标很快就能求出kA1P·kA2P的值为定值．

在此基础上，笔者设计了如下问题：

师：（1）将“证明：kA1P·kA2P为定值”改为“探究kA1P·kA2P是否为定值”．

（2）将长轴A1A2改为短轴B1B2，那么kPB1·kPB2是否为定值呢？

（3）在探究过程中大家能否发现、提出更多值得我们研究的问题呢？

学生在“问题链”和“变式设问”的引导下，步步深入，真正地“动”起来．

2．“动”的延伸——意义建构

学生的思维激情一旦被激起，通过自主探究思考，他们肯定会积极交流自己的思考成果，主动展示自己解决问题的思路、方法，甚至是探求中的困惑．通过独自思考，再交流探究，学生不仅掌握了问题的多种求解方法，拓展了解题思路，更为重要的是激起了学生的思维激情，逐步形成了探究的意识，将学生思维的“动”进一步调动起来，同时在“动”的过程中，进一步挖掘数学问题的本质，有时也可发现学生的知识缺陷和思维水平的差异．

在研究了长轴的两个端点改为短轴两个端点后，我们知道kPB1·kPB2为定值，并且定值与kA1P·kA2P的定值相等．

师：这个定值到底与什么有关？能否将此结论推广到一般情形呢？

师：此结论是正确的．探究方向是：从特殊到一般的探究．能否类比到双曲线得出类似的结论呢？反之，若A（1－a，0）、A（2a，0），直线PA1、PA2的斜率乘积为－，则动点P的轨迹是什么？

学生独立求解后发现轨迹是椭圆，并且点B、C是椭圆长轴的端点．根据刚才的研究学生也提出了下列结论：

若A（1－a，0）、A（2a，0），直线PA1、PA2的斜率乘积为，则动点P的轨迹是以A1、A2为实轴端点的双曲线．

师：请同学们根据刚刚的探究过程思考研究这类圆锥曲线的有关问题的方法．

生：（1）设点法；

（2）判断曲线是否为圆锥曲线的依据有：一是圆锥曲线的定义；二是根据所求轨迹的方程．

3．数学应用，触类旁通

反思1：结论推广

问题若A1（－a，0）、A2（a，0），直线PA1、PA2的斜率乘积为m（m≠0、－1），求动点P的轨迹．

结论 当m＞0时，轨迹为双曲线，A1、A1是双曲线的顶点；当m＜0且m≠－1时，轨迹为椭圆，A1、A2是椭圆长轴的两端点．

反思2：类比探究

（1）求椭圆C的方程；

（2）E、F是椭圆C上的两个动点，如果直线AE的斜率与AF的斜率互为相反数，证明直线EF的斜率为定值，并求出这个定值．

学生首先独自思考，然后小组合作交流探究．

探究：（1）由焦点（－1，0）、（1，0）得到那些结论呢？

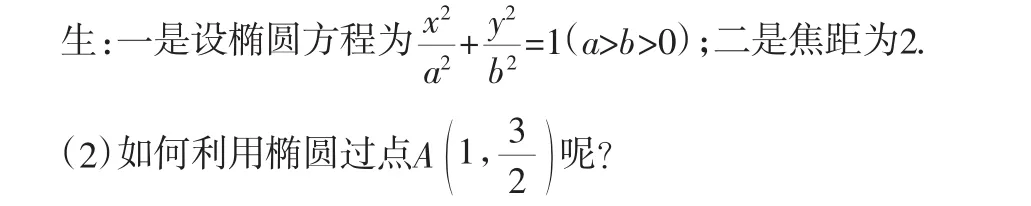
生：一是设出椭圆方程，将点代入方程；二是利用定义求出2a．

（3）求出点E的坐标后，还需要再用刚刚的方法求点F的坐标吗？

生：根据“对称性”，将点E的坐标中k替换为－k，可以直接求出点F的坐标．

师：联想到圆的有关性质：在圆中，圆上任意一点P作两条斜率互为相反数的直线分别交圆于另一点为E、F，则EF的斜率为定值．在椭圆中也有类似的性质．

（4）圆中还有其他有关性质能够类比到圆锥曲线中来吗？

生：过圆上一点引两条互相垂直的直线分别交圆于E、F，由∠EPF=90°，得EF始终为直径，即EF恒经过圆心．

结论 过椭圆上任意一定点A，引互相垂直的两条弦AB、AC，则BC恒过定点．

在“动感数学”课堂教学中，如何激发学生学习的积极性，向学生提供充分经历应用数学活动的机会，主动帮助他们在“动感”过程中真正理解和掌握基本的数学知识与技能，经历过程积累方法，发展思维，培养创新意识，成为数学教师新课程理念下的重要责任．

1．朱占奎．简化课堂教学约定教学文化［J］．中学数学教学参考，2011（3）：8－13．

2．沈红霞．探究能力培养例说［J］．数学通报，2011（10）：26－28．