对一道竞赛试题的再探究

☉浙江省嘉兴二十一世纪外国语学校 郑栋栋

图1

题 目：如图1，在平行四边形ABCD中，△ABE和△BCF都是等边三角形.求证：△DEF是等边三角形.（《全国初中数学竞赛辅导》初二第12讲）

本题将特殊三角形和特殊四边形结合起来，将其设计成一道探索性较强、解法较多的竞赛培训题，然而试题预留了继续探究的空间.本文将逐步探索以平行四边形的四条边向外（内）作特殊三

角形，所形成的图形之间的面积关系.现由笔者整理如下.

一、向内作等边三角形

为了叙述方便，先给出下列定义：①以平行四边形的四条边为边分别向外（内）侧作三角形，顺次连接四个三角形的顶点（不包括平行四边形的四个顶点）所得的四边形称为外（内）构四边形；②所作的三角形称为外（内）延三角形.

如图2，若以平行四边形ABCD的边AB、BC、CD、DA为边分别向内侧作等边三角形，得到的顶点分别为E、F、G、H，顺次连接这四个点，得内构四边形EFGH.

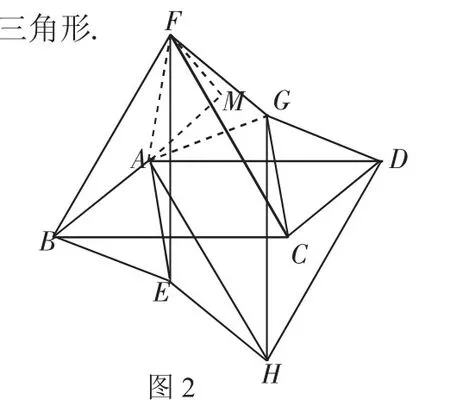
探索1：易证△FBE≌△HDG，得FE=HG，同理可得FG=HE，即四边形EFGH是平行四边形.现探究内构四边形与内延三角形的面积关系.为了便于表述，这里设AB=a，BC=b，∠ADC=α（0°＜α≤90°），下同.

（1）当0°＜α≤60°时，连接AF，AG.

因为AB=CG=a，BF=CF=b，

又因为∠FBA=∠FBC-∠ABC=60°-α，

∠FCG=∠BCD-∠FCB-∠GCD=60°-α，

所以△FBA≌△FCG，所以FA=FG.

同理△FBA≌△ADG，所以FA=AG.

所以△FAG是正三角形.

延长BA，过点F作FM⊥BA，垂足为M，则：

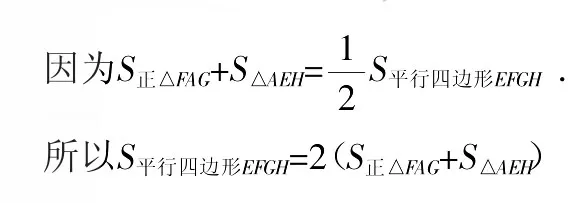
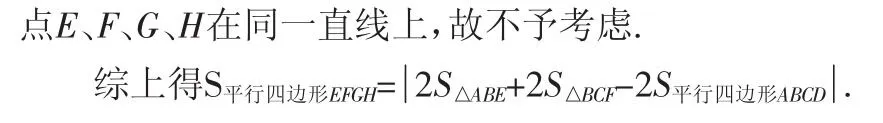
根据上面的探索和定义有下命题.

命题1：当内延三角形是等边三角形时，内构四边形的面积为所有内延三角形的面积与平行四边形面积的两倍之差的绝对值.

二、向外作等边三角形

如图3，以平行四边形ABCD的边AB、BC、CD、DA为边分别向外侧作等边三角形，得到的顶点分别为E、F、G、H，顺次连接这四个点，得四边形EFGH.

探索2：易证△EBF≌△GDH，得EF=GH，同理可得EH=GF，则四边形EFGH是平行四边形.现探究外构四边形与外延三角形的面积关系.

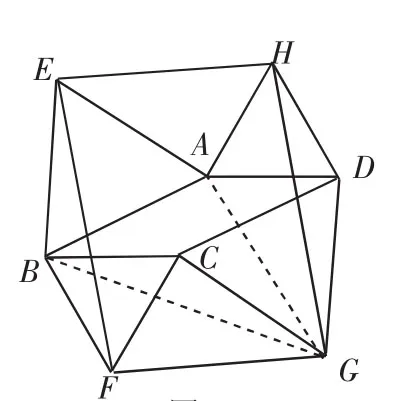
图3

（1）当0°＜α≤60°时，在平行四边形ABCD中AB∥CD，∠BAD=180°-∠ADC=180°-α.

因为△HAD和△EAB是等边三角形，

所以∠HAD=∠EAB=60°.

因为∠HAE=360°-∠HAD-∠EAB-∠BAD=60°+α，

∠ADG=∠CDG+∠ADC=60°+α，

所以∠HAE=∠ADG，所以△HAE≌△ADG.

同理可得△HDG≌△GCB.

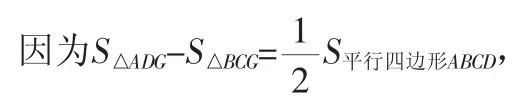
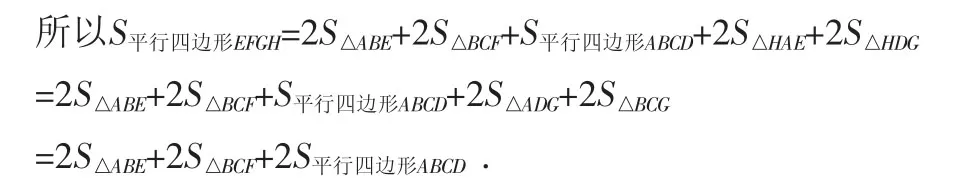
命题2：当外延三角形是等边三角形时，外构四边形的面积为所有外延三角形的面积与平行四边形面积的两倍之和.

探索3：当外延三角形是等边三角形时，由命题2可知：

三、向内作等腰直角三角形

如图4，若以平行四边形ABCD的边AB、BC、CD、DA为斜边分别向内侧作等腰直角三角形，直角顶点分别为E、F、G、H，顺次连结这四个点，得内构四边形EFGH.

探 索4： 易 证 △HAE≌△HDG，得HE=HG，同理可得HE=HG=FG=FE，即四边形EFGH是菱形.而∠AHG+∠GHD=90°，则∠AHG+∠AHE=90°，则四边形EFGH是正方形.

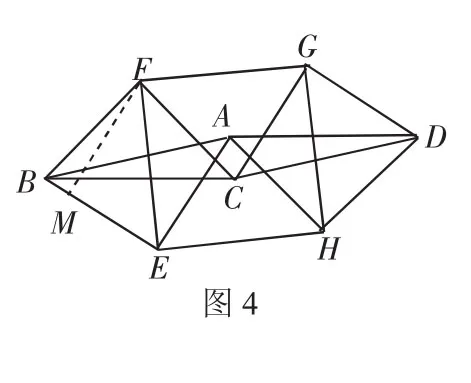
探索内构四边形与内延三角形的面积关系.

（1）当0°＜α≤45°时，过点F作FM⊥BE，垂足为M.

因为∠FBE=∠FBC+∠ABE-∠ABC=90°-α，

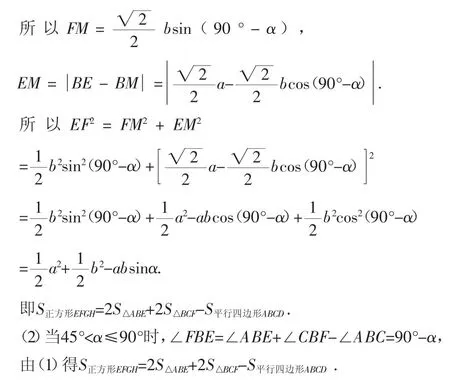
于是综上情况可得命题3.

命题3：当内延三角形是等腰直角三角形时，内构四边形的面积为所有内延三角形的面积与平行四边形面积之差.

四、向外作等腰直角三角形

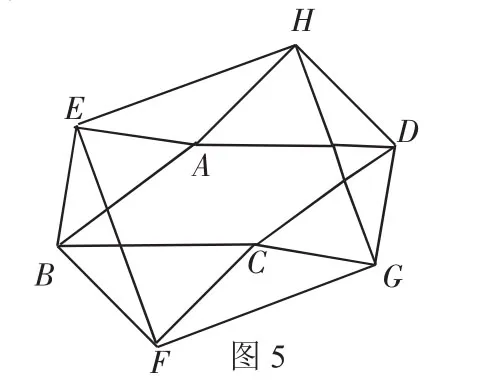
如图5，若以平行四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形，直角顶点分别为E、F、G、H，顺次连结这四个点，得外构四边形EFGH.

探索5：易证△HAE≌△HDG，得HE=HG，同理可证四边形EFGH是菱形.而∠AHG+∠DHG=90°，则∠AHG+∠AHE=90°，即四边形EFGH是正方形.于是：

命题4：当外延三角形是等腰直角三角形时，外构四边形的面积为所有外延三角形的面积与平行四边形面积之和.

探索6：当外延三角形是等腰直角三角形时，由命题4可知