一种开放系统非平衡态气体的状态方程

吴竹歆

西安理工大学，陕西西安 710054

0 引言

现在的理想气体状态方程和多变方程等都是以一定气体的封闭系统为研究对象，所描述的状态是整个封闭系统整体的状态，而无法深入研究某一细微处的状态规律。本文在气体稳态导热给定边界条件的情况下，给出了描述微观开放系统的非平衡态气体状态方程，并做了cfd软件模拟分析和运用此公式推导高精确度热导率公式的验证，期望以此两种方法证明此公式的正确性，并确定它的适用范围。本文的重点是在给出此公式后进行的正确性和精确度验证。

气体在两平板间稳态导热时，若两平板温度给定并且恒定，则其间气体状态参数近似服从方程式每一不同温度处的气体实际上处于开放系统中，整个系统是非平衡态的。

现在以氢气为例进行验证：

如图1所示的系统中：

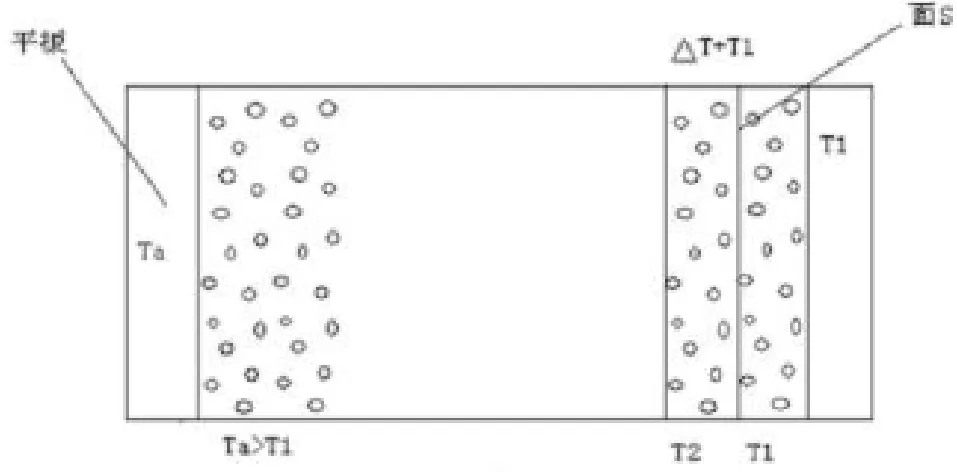
图1

1 cfd软件模拟分析验证

以上所得的压强值与cfd软件模拟值非常接近，证明此公式精确度较高。但由于cfd软件模拟分析中未考虑热辐射，因此模拟出的压强比实际压强偏底，并随着温度的上升辐射强度增大，模拟误差将越来越大。因此此公式的精确度实际上会更高。

2 用此公式推导气体热导率公式并验证其精确度

下面再用此公式推导气体热导率计算式：

以图一所示系统为研究对象,有

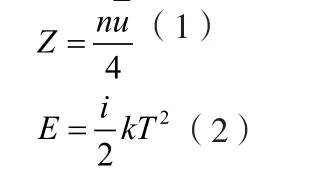
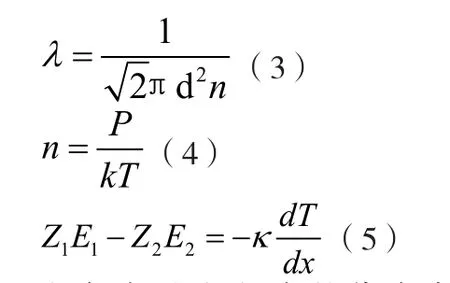
注意式子（1）中的代表穿过面1的气体分子数，它们已经迁移进入了另一个微小单元体，不属于某一处流动着气体，以他们为对象是以一定量的气体分子为研究对象，仍满足理想气体状态方程，因此有式（4）。而公式所描述的对象则是此系统中固定某一位置截面处微小体积内的气体，其中的分子是不断交换变化的，此微小体积属于开放系统。

根据傅立叶定理建立导热微分方程：

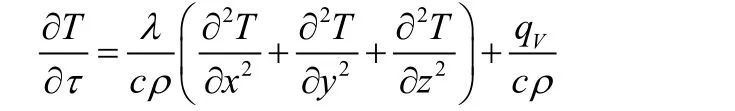
在稳态，无内热源的情况下，有

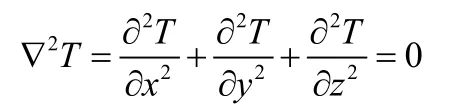
可知平板内气体温度呈线性分布。引入参数，有

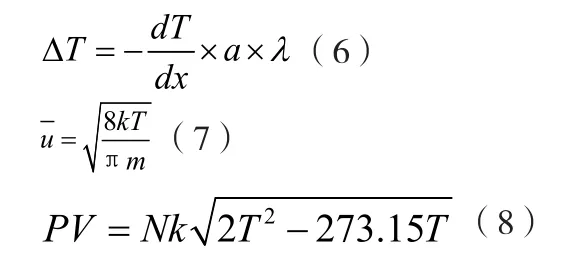
联立（1）～（5）式和（7）式可解得：

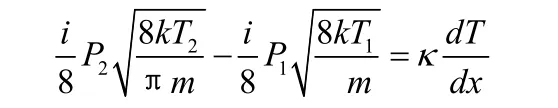
因为此系统内压强变化非常小，因此令 P2≈P1=P，上式可化简为

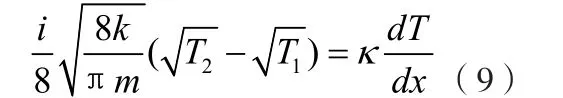
把（6）式代入（9）式，注意此时的属于固定截面1附近的开放系统的分子数密度，因此此处应联立式（8），化简可得下式：

现在检验此公式的精确度并与以往公式作比较：

以往的一种气体热导率公式为

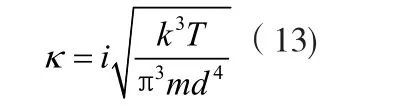
以氢气为例 ，d = 2.3× 10(-23)m,i = 5:

当 T = 273.15K时，式（12）计算得，检测值0.172，公式（13）计算值0.249

当 T = 373.15K时 ，式（12）计算得检测值0.220, 公式（13）计算值0.29

当 T = 473.15K时 ，式（12）计算得检测值0.264, 公式（13）计算值0.327

以往的气体热导率计算公式有几种（包括理论推导出的和经验半经验的公式），但它们所计算出的结果皆与实际检测值相差较远，且有的计算起来非常麻烦，在这里就不一一列举了，读者有兴趣可以自己查找并校验一下便知。但此热导率计算公式形式比较简单，而且精确度比以往的都高很多，可以说达到了比较精确的程度。

关于如何推导更加精确的气体热导率公式，笔者将在另一篇文章里结合对流换热等知识进行详细的论述。

3 验证结果的总结

通过以上两种方法的验证，充分说明当气体处于稳态导热，边界上的温度给定并且恒定时，非平衡态的相对开放系统的气体状态参数近似服从公式。可以看出，当温度升高时，此公式的精确度将缓慢下降，但在673.15K以内，此公式精确度都较高，值得应用。

4 结论

以往气体状态方程都是以一定气体的封闭系统为研究对象，所描述的是一个宏观状态的热力学参数。本文以气体稳态导热的任何一个微小体积为研究对象，实际上是一种非平衡态开放系统。在给出此开放系统的状态方程后，用了两种方法对此方程进行了验证。验证结果与测量结果都非常接近，由此可知本公式是正确的。由于非平衡态开放系统气体分子运动相当复杂，而本公式描述的对象又只是理想气体，因此本公式仍有相对误差，并且随着温度的上升误差在缓慢增大。但在温度不是特别高的情况下（一般在673.15K以内），本公式误差仍然很小，在此范围内一般都可适用。

[1]东南大学等七所工科院校编，马文蔚，解希顺，周雨青等改编.物理学[M].5版（下册）.北京：高等教育出版社，2006.

[2]傅秦生.热工基础与应用[M].2版.北京：机械工程出版社，2009.

[3]陈涛，张国亮.化工传递过程基础[M].3版.北京：化学工业出版社，2009.