习题课是民族班“力学”教学的重要组成部分

热依汗.依不拉依木，陈国新

（新疆农业大学 水利与土木工程学院，新疆 乌鲁木齐 830052）

力学课是理论性较强且比较难学的课程，因而在一般院校中所遇到的一些问题，如内容多、学时少、听课容易，解题难等问题，在少数民族班学生中就更为突出了。笔者二十几年的力学教学实践中深深体会到，上好“理论力学”习题课是非常重要的，尤其对少数民族班学生来说，可以通过习题课消化，理解所学的知识，深化理论，再由理论来解决实际问题，形成理论——习题——理论的教学方式。

1 选工程中常见且难度适中的例题

在学习静力学物系平衡问题的习题课上，我们常以工程中常见的起重机的受力分析为例题进行讲解，见图1所示，起重机放在AB组合梁上，重力Q作用线通过C，题目要求计算A和B处的约束力.先取梁上面的起重机为隔离体，计算约束力NE和NF，然后分析ACB组合梁。经分析有四个约束力，但整体只有三个平衡方程如何求截呢？对这一问题可有两种途径解决。

第一种途径，首先以CB部分为研究对象，求得未知力NB，然后再取整体AB，应用三个平衡方程，即可求出未知力XA、YA和 MA。

第二种途径，分别以各部分（BC，AC）为研究对象，先取CB 部分，利用三个平衡方程，求得 NB，XC，YC。然后把 XC，YC反向加在AC部分上作为载荷，由AC部分求出其它三个未知力，在计算过程中，额外求解了题目并不需要的约束力XC，YC，使计算繁锁。

图1 起重机受力图解

通过比较以上两种求解方法，使学生领悟到:①力学计算的方法不是唯一的。②认真分析题意，采用简单方法。

2 通过讨论课解决疑难问题

在讲课中，采用启发式教学，引导学生分析问题和思考问题，使学生既不感到纯理论方面内容的枯燥乏味，也避免陷入繁杂的数学分析和公式推导之中，例如:讲点的复合运动时，概念多，难度大。特别是牵连运动，虽然概念是从各种实例中引出的，但仍然有相当一部分学生复合运动的概念理解不透，为此在习题讨论课上我们选择典型习题进行详尽分析，力争让学生对动点，动系的选取有一个深入的了解。

例如:图2所示偏心凸轮中关于动点，动系的选择分析。动点——因为AB杆上的点始终不应离开偏心轮的圆（即相对轨迹是圆）而偏心凸轮又在运动，所以选AB杆上的A点为动点。

动系——固结在凸轮上，随凸轮绕O轴转动。

若选凸轮上与A点重合的A謖点为动点，则必须选动杆AB为动系，A謖点的相对轨迹是一条曲线，无法直接判断出来，只能由解析法算出A謖点的相对运动方程，再求得相对运动轨迹。对于求加速度，由于A謖点相对轨迹的曲率半径难以确定，求加速度比较困难，故这种选择动点和动系的方法，虽然求速度时可以用，但在求加速度时是不可取的。

从本题可见，当动点，动系选的不合适，即相对轨迹不能直接判断时计算加速度的工作将要增加许多，这是不可取的。

动力学中的综合题大部分是比较复杂的问题，往往不是应用某一定理所解决的，需要联合应用几个定理求解。

例如图 3所示（a），（b）两题中，各轮的质量相同，直径相同，C1和C2轮都作平面运动，静止落下，落下的距离都为h时求，VC1，VC2与 h 的关系。

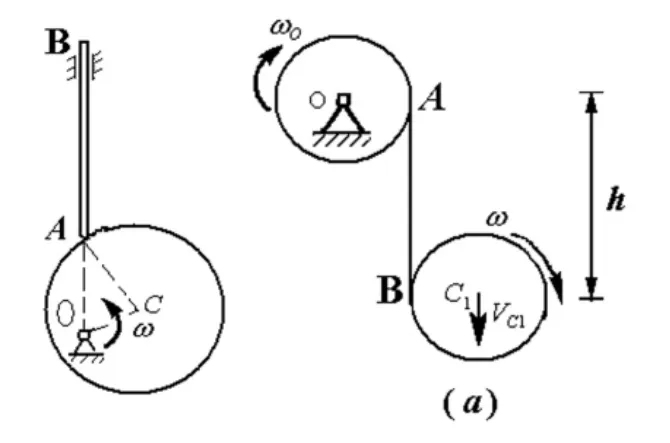
图2 偏心凸轮图解

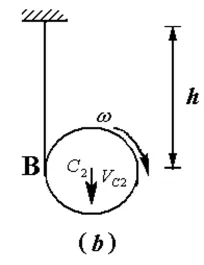
图3 力学图解

求解这类动力学问题的关键是先解决运动学关系，那么C1和C2轮质心的速度是否相同呢？在（a）题中，O轮绕定轴转动，使绳具有速度，以B点为基点它的运动学关系是VC1=Rω-O+RωC，其中ωO，ωC都是未知量。为此必须设法应用其它动力学理论来找出他们的关系。分别取O轮和C1轮为研究对象，由定轴转动及平面运动的微分方程求出ωO=ωC=ω，所以对（a）图VC1=2Rω

对（b）题，绳是不动的，B点为速度舜心VC2=Rω所以质心的速度是不同的，在写动力学方程时，也就不能一概而论，而要具体问题具体分析。

3 结语

通过上面例题的比较，提高了学生分析问题和解决问题的能力，同时提高了学生的解题兴趣。学生在学习力学的复杂问题时，对于基本结构的选取和解题思想上缺乏深刻了解，为了保证力学内容的讲授，我们同时安排辅导课和习题课，解决力学学习中的疑难问题，学好专业基础课是能否学好专业课的重要环节，特别是像这样与工程实际有密切关系的专业基础课。它不仅对相关专业课的学习很有帮助，而且对培养实践能力更加重要。所以教师要讲清基本概念，内容和技能，学生要积极配合，多动手练习，才能掌握这种技巧，要通过辅导课和习题课以达迅速，为后续学习奠定基础。

[1]谢传锋.理论力学自我监测[M].北京:航空学院出版社，2003.

[2]热依汗.关于力学教学法的探讨[J].新疆农业大学学报，2000.

[3]程靳等.理论力学学习辅导[M].北京:高等教育出版社，2009.