强Gorenstein投射和内射复形

张东东，欧阳柏玉

（1．浙江师范大学数理与信息工程学院，中国金华 321004；2．湖南师范大学数学与计算机科学学院，中国长沙 410081）

强Gorenstein投射和内射复形

张东东1，2，欧阳柏玉2*

（1．浙江师范大学数理与信息工程学院，中国金华 321004；2．湖南师范大学数学与计算机科学学院，中国长沙 410081）

分别研究了Gorenstein投射和内射复形的特殊情况：强Gorenstein投射复形和强Gorenstein内射复形．证明了复形C是Gorenstein投射复形当且仅当它是强Gorenstein投射复形的直和项．同时，证明了若R在左Noetherian环下，下有界复形C是强Gorenstein内射复形当且仅当C是正合的且每一项Ci是强Gorenstein内射R-模．

强Gorenstein投射（内射）复形；Gorenstein投射（内射）复形

1 Introduction

Throughout this paper，R denotes an associative ringwith identity and allmodules are left R-modules．A complex

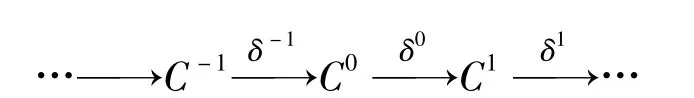
of left R-moduleswill be denoted by C．Wewill use subscripts to distinguish complexes：for example，if{Ci}i∈Iis a family of complexes，Ciwill be

Given a left R-modulem，we will denote bythe complex

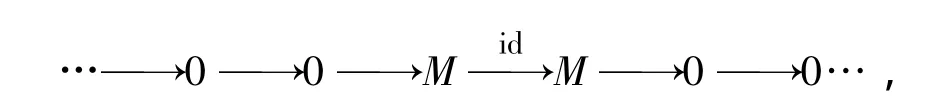
with the firstMis－1 position．Given a complex C and an integerm，C［m］denotes the complex such that C［m］n=Cm+nand whose boundary operators are（－1）mδm+n．

A complex C is called bounded above when Ci=0 for i≫0，bounded below when C－i=0 for i≫0 and，bounded when it is both bounded above and below．

C is called a projective（resp．，injective）complex if C is an exact complex and every kerδiis a projective（resp．，injective）module．

In1960's，Auslander and Bridger introduced a homological dimension，called G-dimension，for finitely generatedmodules over commutative Noetherian rings［1-2］．Several decades later，this homological dimension was extended to Gorenstein dimension ofmodules by Enochs et al．［3-5］．In2004，Holm［6］generalized several results which are already obtained over Noetherian rings to associative rings．Recently，Bennis andmahdou［7］introduced a special case of Gorenstein projective（resp．，injective，flat）modules，which are called strongly projective（resp．，strongly injective，strongly flat）modules．The principal role of the strongly Gorenstein projectivemodules is to give the characterization of Gorenstein projectivemodules（see［7，Theorem2．7］）．Meanwhile，strongly Gorenstein projectivemodules have simpler characterizations than their correspondent Gorensteinmodules（see［7，Propositions2．9］）．For instance，amoduleMis strongly Gorenstein projective if and only if there exists a short exact sequence ofmodules 0→M→P→M→0，where P is projective，and Exti（M，Q）=0 for any i≥1 and any projectivemodule Q．Using the results above，the notion of strongly Gorenstein projectivemodulewas proven to be a good tool for establishing results on Gorenstein projective dimensions（see［8］）．

According to［9］，a complex C is called Gorenstein projective if there exists an exact sequence of projective complexes

with C=ker（P0→P1）and Hom（－，Q）leaves the sequence P exact whenever Q is a projective complex．The exact sequence P is called a complete projective resolution of complex．

The Gorenstein injective complex is defined dually．

In this paper，we introduce a special case of Gorenstein projective（resp．，Gorenstein injective）complex，which is called strongly Gorenstein projective（resp．，strongly Gorenstein injective）complex．We show that strongly Gorenstein projective（resp．，strongly Gorenstein injective）complex has similar property of strongly Gorenstein projective（resp．，strongly Gorenstein injective）module．Meanwhile，we show that，over a left Noetherian ring，a bounded below complex C of left R-modules is strongly Gorenstein injective if and only if C is an exact sequence and Ciis strongly Gorenstein injective R-module for all i∈Z．

General backgroundmaterials can be found in［10～13］．

2 Strongly Gorenstein projective and injective complexes

Definition1 A complete projective resolution of complex of the form

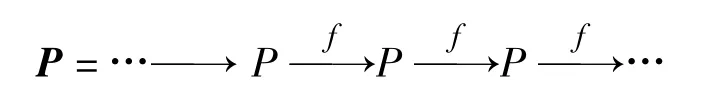
is called strongly complete projective resolution of complex and denoted by（P，f）．

The complex Ker f=IMf is called strongly Gorenstein projective complex associated to（P，f）．A complex C≅Ker f（IMf）is said to be a strongly Gorenstein projective complex．The strongly Gorenstein injective complex is defined dually．

It is straightforward that the strongly Gorenstein projective（resp．，strongly Gorenstein injective）complex is a special case of the Gorenstein projective（resp．，Gorenstein injective）complex．And it is well known that every projective（resp．，injective）complex is Gorenstein projective（resp．，Gorenstein injective）complex．We will seethat every projective（resp．，injective）complex is strongly Gorenstein projective（resp．，strongly Gorenstein injective）complex by Remark1．Hence the class of all strongly Gorenstein projective complexes is an intermediate class between the ones of projective complexes and Gorenstein projective complexes which are，in general，strict by Examples1 and2．

Proposition1（1）If（Pi）i∈Iis a family of strongly Gorenstein projective complexes，then⊕Piis a strongly Gorenstein projective complex．

（2）If（Ii）i∈Iis a family of strongly Gorenstein injective complexes，thenΠIiis a strongly Gorenstein injective complex．

ProofIt is easy to obtain by the definitions of strongly Gorenstein projective complex and strongly Gorenstein injective complex．

Theorem1A complex is Gorenstein projective complex if and only if it is a direct summand of a strongly Gorenstein projective complex．

ProofIt remains to prove the direct implication by［6，Theorem2．5］．

Let C be a Gorenstein projective complex．Then there exists a complete projective resolution of complex

Now we give some characterizations of strongly Gorenstein projective complex．

Proposition2For any complex C，the following are equivalent：

（1）C is a strongly Gorenstein projective complex；

（2）There exists a short exact sequence of complexes0→C→P→C→0，where P is a projective complex such that Exti（C，Q）=0 for all i≥1 and any projective complex Q；

（3）There exists a short exact sequence of complexes0→C→P→C→0，where P is a projective complex such that Exti（C，Q）=0 for all i≥1 and any complex Q with finite projective dimension；

（4）There exists a shortexact sequence of complexes0→C→P→C→0，where P is a projective complex，and Ext1（C，Q）=0 for any projective complex Q；

（5）There exists a shortexact sequence of complexes0→C→P→C→0，where P is a projective complex，and Ext1（C，Q）=0 for any projective complex Q with finite dimension；

（6）There exists a short exact sequence of complexes0→C→P→C→0，where P is a projective complex such that Exti（C，Q）=0 for some i≥1 and any projective complex Q；

（7）There exists a short exact sequence of complexes0→C→P→C→0，where P is a projective complex such that Exti（C，Q）=0 for some i≥1 and any projective complex Q with finite dimension．

ProofThe proof is similar to that of［7，Proposition2．10］and［8，Remark2．3］．

ReMark1Note that every projective complex P is strongly Gorenstein projective by Proposition2．Indeed，we have the short exact sequence 0→P→P⊕P→P→0 and Ext1（P，N）=0 for any complex N．

Proposition 3If C is a strongly Gorenstein projective complex，then every Ciis a strongly Gorenstein projectivemodule and Hi（C）≅Hj（C）for any i，j∈Z．

ProofIf C is a strongly Gorenstein projective complex，then there exists an exact sequence of complexes0→C→P→C→0，where P is a projective complex such that Ext1（C，Q）=0 for any projective complex Q．Since P is a projective complex，P is an exact complex．So we have Hi（C）≅Hi+1（C）for any i∈Z by long exact sequence theorem．Hence we have Hi（C）≅Hj（C）for any i，j∈Z．

For anymodule Ci，we have an exact sequence ofmodules 0→Ci→Pi→Ci→0 with a projectivemodule Pi．For any projectivemodule Q，Ext1（C［i－1］）=0 since［i－1］is a projective complex．So we have Ext1（Ci，Q）=0 and Ciis a strongly Gorenstein projectivemodule by［7，Proposition2．9］．

Remark2Duallywe can characterize the strongly Gorenstein injective complex as in Proposition2，and similar results for strongly Gorenstein injective complex as in Proposition 3．

Lemma1IfMis a strongly Gorenstein projectivemodule，then［n－1］is a strongly Gorenstein projective complex．In particular，ifMis a Gorenstein projectivemodule，then［n－1］is a Gorenstein projective complex．

ProofSinceMis a strongly Gorensteinmodule，then there exists an exact sequence ofmodules0→M→P→M→0 with P a projectivemodule．Hence we have the following exact sequence of complexes 0→→→→0，whereis a projective complex．Dual to the proof of［14，TheoreM8］，we have Ext1（，Q）=0 for any projective complex Q，henceis a strongly Gorenstein projective complex．

IfMis a Gorenstein projectivemodule，thenMis a direct summand of strongly Gorenstein projectivemodule N by［7，Theorem2．7］．Thenis a strongly Gorenstein projective complex by above．It is easy to check thatis a direct summand of，thenis Gorenstein projective complex by Theorem1，as desired．

ExaMple1Consider the quasi-Frobenius local ring R=k［X］/（X2）where k is a field，and denote by{X} the residue class in R of X．

（2）But it is not a projective complex．

Proof（1）（{X}）is a strongly Gorenstein projectivemodule by［7，Example2．5］．Henceis a strongly Gorenstein projective complex by Lemma1．

（2）（{X}）is not a projectivemodule by［7，Example2．5］，henceis not a projective complex．

ExaMple2Consider the local ring R=k［［X1，X2，…］］/（X1X2），where k is a field，and denote by{Xi} the residue class in R of Xifor i=1，2．Then

（2）They are not projective complexes．

Proof（1）Since（{Xi}）are Gorenstein projectivemodules，thenare Gorenstein projective complexes by Lemma1．

ExaMple 3Let R be a left Noethereian ring andMa nonzero Gorenstein injectivemodule．Then the complex X=0→M→0 withMin the 0 position is a Gorenstein injective complex which is nota strongly Gorenstein injective complex．

ProofThe complex X is a Gorenstein injective complex by［14，TheoreM8］．It is clear that H0（X）=M≠0，so X is not a strongly Gorenstein injective complex by Remark2．

By Remark2，we know that if C is a strongly Gorenstein injective complex，then Ciis a strongly Gorenstein injectivemodule and Hi（C）≅Hj（C）for any i，j∈Z．It is natural to ask：Is the strongly Gorenstein injective exact？We give a negative answer by the following example．

ExaMple4Let R be a left Noetherian ring，and I an injective R-module．Then the complex

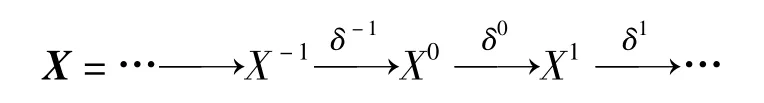
with Xi=I andδi=0 for any i∈Z is strongly Gorenstein injective complex，which is not an injective complex．

ProofSince X is not exact，X is not an injective complex．Let

be a complex such that Yi=I⊕I andηi：I⊕I via（a，b）→（0，a）for any i∈Z．It is easy to check that Im（ηi）= 0⊕I=Ker（ηi+1）≅I．Hence Y is an injective complex．

Consider the following diagram

such that fi：I→I⊕I via a→（0，a）and gi：I⊕I via（a，b）→a for any i∈Z．It is easy to check that the above diagraMis commutative and 0→X→Y→X→0 is an exact sequence of complexes．X is a Gorenstein injective complex by［14，TheoreM8］since each Xiis Gorenstein injective，and Ext1R（E，X）=0 for any injective complex E．So X is a strongly Gorenstein injective complex by Remark2，as desired．

［1］ AUSLANDERm．Anneaux de gorenstein，et torsion en algèbre commutative［J］．Séminaire d'Algèbre Commutati Samuel，1966，1：2-69．

［2］ AUSLANDERm，BRIDGERm．Stablemodule theory［M］．Providence：Americanmathematical Society，1969．

［3］ ENOCHSE E，JENDA OMG．On Gorenstein injectivemodules［J］．ComMAlgebra，1993，21（10）：3489-3501．

［4］ ENOCHSE E，JENDA OMG．Gorenstein injective and projectivemodules［J］．Math Z，1995，220（1）：611-633．

［5］ ENOCHSE E，JENDA OMG，TORRECILLASB．Gorenstein flatmodules［J］．Nanjing Daxue Shuxue Bannian Kan，1993，10（1）：1-9．

［6］ HOLMH．Gorenstein homological dimensions［J］．JPure Appl Algebra，2004，189（1-3）：167-193．

［7］ BENNISD，MAHDOU N．Strongly Gorenstein projective，injective，and flatmodules［J］．JPure Appl Algebra，2007，210（2）：437-445．

［8］ BENNISD，MAHDOU N．Global Gorenstein dimensions［J］．Proc Amermath Soc，2010，138（2）：461-465．

［9］ ENOCHSE E，GARCIA ROZAS JR．Gorenstein injective and projective complexes［J］．ComMAlgebra，1998，26（5）：1657-1674．

［10］ CHRISTENSEN LW．Gorenstein dimensions［M］．Berlin：Springer，2000．

［11］ ENOCHSE E，JENDA OMG．Relative homological algebra［M］．New York：Walter de Gruyter，2000．

［12］ GARCIA ROZAS JR．Covers and envelopes in the category of complexes ofmodules［M］．Boca Raton：CRC Press，1999．

［13］ XU JZ．Flat covers ofmodules［M］．Berlin：Springer，1996．

［14］ LIU Z K，ZHANG CX．Gorenstein injective complexes ofmodules over Noetherian rings［J］．JAlgebra，2009，321（5）：1546-1554．

（编辑 沈小玲）

Strongly Gorenstein Projective and Injective Complexes

ZHANG Dong-dong1，2，OUYANG Bai-yu2*
（1．Department ofmathematics，Zhejiang Normal University，Jinhua 321004，China；
2．College ofmathematics and Computer Science，Hunan Normal University，Changsha410081，China）

A special case of Gorenstein projective，and injective complexes，which are called strongly Gorenstein projective and injective complexes，are studied respectively．It is proved that a complex C is a Gorenstein projective if and only if it is a direct summand of a strongly Gorenstein projective complex．Meanwhile，it is shown that，over a left Noetherian ring，a bounded below complex C of left R-modules is strongly Gorenstein injective if and only if C is an exact sequence and Ciis a strongly Gorenstein injective R-module for all i∈Z．

strongly Gorenstein projective（injective）complex；Gorenstein projective（injective）complex

O154．2

A

1000-2537（2012）04-0001-05

2011-11-22

国家自然科学基金资助项目（10901141）

*通讯作者，E-mail：oy@hunnu．edu．cn