工业过程中的控制策略研究
2012-08-22魏权利王西庚
魏权利 王西庚
(青岛科技大学信息学院 山东 青岛 266061)
0 引言
工业过程中的控制是工业过程控制领域中一个具有挑战性的任务,很难采用简单的集中控制方法或建立精确的机理模型。而分散控制策略和智能控制方法就成为解决这类问题的最好选择之一。分散控制策略能够将复杂问题简单化,便于进一步的研究和分析;而智能控制方法则无需建模,将难以解决的问题仅仅通过学习就得到了有效地处理,提供了解决复杂问题的又一途径。
本文中,首先介绍了分散预测控制的基本概念,叙述了粗糙控制的发展。然后针对复杂大系统内部快慢特性不一的特点,提出了一种基于纳什最优的多时标分散预测控制算法。同时,通过引入多时标信息预估和通信方法,弥补了由于时标不同而导致子系统信息不足的问题,提高了控制效果。最后对先进控制策略进行了介绍。
1 工业过程中的控制策略
1.1 分散预测控制
分散控制本质上是指利用分散的信息实现分散的控制,以实现利用多个地域分散的局部控制器取代单一的集中控制器进行控制,每个控制器以基于局部测量得到的输出信息控制相应子系统的输入。
预测控制,也称为模型预测控制(MPC)具有控制效果好、鲁棒性强、能够有效克服过程的不确定性、非线性以及处理各种约束等优点。预测控制算法种类较多、形式各样,比较流行的算法有动态矩阵控制(DMC)、模型算法控制(MAC)、广义预测控制 (GPC)等等,其实现机制都包括三部分:预测模型、滚动优化、反馈校正。预测控制系统的结构如图1.1所示。
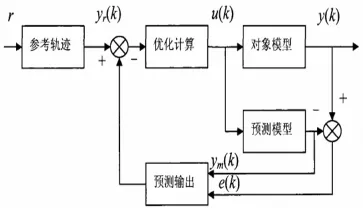
图1.1 预测控制系统结构图
根据被控对象的特性要求不同,局部控制器可以是单变量的PID控制器也可以是多变量的MPC控制器。由于预测控制的成功应用,许多学者把它应用于分散结构的控制系统之中。有些学者提出了一种分散MPC算法,其中子系统的动态特性和性能函数都独立于其他子系统的变量,但是通过约束连接不同子系统之间的状态和控制变量,鲁棒可行性在假设干扰独立有界时得到了保证。
1.2 智能控制简介
智能控制方法能够模拟人类的思维方法,在无需获知控制对象内部机理以及外部扰动的前提下,它仍可利用对象的输入输出特性的分析设计出切实可用的控制器,取得预期目的。当前,智能控制的领域主要包含自适应控制、粗糙控制、神经网络控制和专家控制等。
自适应控制:自适应控制能够修正系统自身的特性以适应对象和扰动的动态特性变化。它所依据的关于模型和扰动的先验知识比较少,可以在系统运行的过程中,通过在线辩识,不断地提取模型的有关信息。
粗糙控制:粗糙控制通过“If…Then…”的方式来表达控制规律,并采用粗糙推理机制提取控制规则,无需建立数学模型神经网络控制:神经网络控制是在神经网络理论与控制理论的融合过程中而产生的。神经网络是一个非线性的动力学系统,其特点和优势在于信息的分布式存储和并行协同处理,可以对不明确的对象进行学习式控制。
专家控制:专家控制系统是一个模拟人类智能的计算机程序系统,其核心部分是专家知识库,存储着大量的代表某个领域专家水平的控制策略。
1.3 粗糙控制
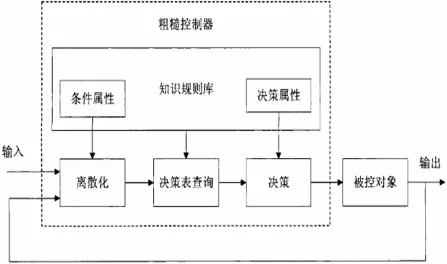
图1.2 粗糙控制流程图
粗糙集理论 (Rough Set Theory,简称 RST)可以仅仅依靠所需处理的数据集合进行信息的处理和学习,而不需要任何其它先验知识,是一种新颖的处理不确定性和模糊性知识的工具。其主要优点如下:
1)无须其他任何的先验知识,仅根据数据本身就能够提取信息;
2)以“lf…Then…”的形式来表达知识和决策规则,非常便于人们理解和使用;
3)能处理和表达不完备信息,并能从经验数据中挖掘潜在的知识和规则。
粗糙控制是指基于粗糙集理论解决控制问题的方法和技术总和。从控制角度来说,粗糙控制是一种利用数据来获取控制策略的“从范例中学习”方法。同时,粗糙控制又是一种基于规则的控制方法,它能从己经观测到的典型数据中学习和提炼规则,并以决策表的方式表达决策规则以进行相应的控制步骤。其流程大致如图1.2所示。
2 多时标分散预测控制算法
多时标分散预测控制算法,针对每个子系统的快慢的特点采取相应的控制策略实现局部控制目标,把一个动态大规模问题分解成一系列小规模耦合的动态子问题。
2.1 预测控制算法
预测控制采取采样算法,在控制的过程中,控制变量u(k)是在每个相同间隔的离散时刻k=0,1,2,…进行决策的。在每个决策时刻k,控制器在模型预测的基础上求解一个未来有限时域内过程对象的动态参数优化问题(DP)以给出相应的控制行为。通过时间的离散化,MPC可以将一个动态控制问题转化为一系列时域滚动向前的静态优化问题,在每个时刻,计算当前时刻的优化命题并预测未来的控制行为。
MPC算法滚动优化的原理可如图2.1所示:
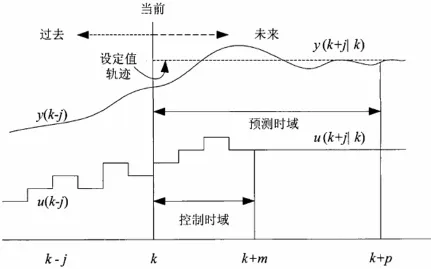
图2.1 MPC算法滚动优化原理图
2.2 Nash最优概念
在分散控制中,各个局部控制器在整个系统中的地位都是相同的,没有一个控制器可以对整个大系统进行控制。由于每个子系统都是相对独立的,它们都有各自想要达到的不同目标,通过执行相对自身的最优策略,每个子系统实现了最好的可能收益,但是由于目标的不一致性和难以协调,往往导致目标之间的冲突。假定第i个控制器的目标可记作为:
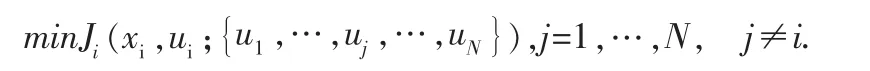
纳什最优解反映了所有分散控制器通过竞争达到的平衡,此时,如果任何其他的子系统保持原来的策略不变,进一步改变u,可以实现在当前条件下的最优局部目标。因此,Nash最优解是一个重要的平衡点,它将所有的子系统“锁定”在一组控制策略上,没有任何一个子系统有企图脱离Nash平衡的动机。各子控制器在优化自身的局部目标时,都需要假定获得其它子系统的Nash最优解的前提下,然后才能得出自身的Nash最优解。在每一时刻,各子控制器通过通信网络获得其他子控制器预估最优解,并据此计算自身的Nash最优解。
2.3 多时标分散预测控制算法
在模型预测中,假定在某个时刻施加一个△u(k)的控制作用之后,控制量不再发生变化,则未来P个时刻的模型输出预测值是过去所有时刻的控制作用累积的结果。从这个原理出发,可以将慢系统的大步长分割成一系列与快系统步长同长度的时间段(虚拟时标)。
多时标分散预测控制算法的步骤大致分为:
步骤1:初始化:根据各子系统不同的快慢特性,分别采用相应的采样时间;并选取具有最小采样时间的快系统作为基准时刻。
步骤2:通信和多时标预估
步骤3:关联作用域形成
步骤4:优化
步骤5:迭代,执行,滚动。
上述多时标分散预测控制算法符合多目标纳什优化思想,最终解为纳什最优解。在k时刻,每个进行决策行为的控制器通过通信或多时标预估得到了所有其它相关联的控制器的最优解,并在此基础上求解自身的纳什最优解;并将新求出的最优解和上次的结果相比较,直至两次迭代结果的误差均满足给定的精度,则说明整个系统达到了纳什平衡。此时没有一个控制器有进一步改变自身控制决策的动机,任何单独改变自身控制决策的行为只能使局部和整体的性能指标变得更坏。
3 先进控制策略综述
先进控制是对那些不同于常规单回路PID控制,并具有比常规PID控制有更好的控制效果的控制策略的统称,而非指某种计算机控制算法。
3.1 先进控制技术
随着MPC(多变量预测控制)技术在实践中的应用与发展,涌现了各种具有MPC思想的先进控制技术,如:模型算法控制(MAC),动态矩阵控制 (DMC)及广义预测控制 (GPC),并且推出了一批商品化的软件产品,例如:DMC、SIMC、RMPCT等。实践证明,这类算法不仅能使生产过程安全可靠的运行,而且能使装置处于最佳运行工况,从而获得显著的经济效益。
内模控制(IMC)是Garcia.C.E和Morari M.受模型算法控制和动态矩阵控制的启发于1982年提出的,由于其设计原理简单,参数整定直观明了,鲁棒性较强,控制性能良好,对纯滞后有补偿作用,一直为工程控制界所重视。近年来,内模控制已经被推广到多变量系统和非线性系统。基于内模控制的PID控制器 (IMC-PID)不但保持了传统PID控制的特点,还具有内模控制的所有优点,而且它的PID形式易于为广大工程技术人员接受和理解,并易于采用现代控制硬件(DCS)来实现和现有控制系统的改造。
3.2 内模控制技术(IMC)
内模控制理论,就是在控制系统中引入了内部模型,使系统的反馈量由常见的输出全反馈变为扰动估计量的反馈。当存在建模误差或干扰时,滤波器发挥作用,抑制干扰或模型失配而引起的实际输出与模型输出之差。这样,系统的设定值响应和干扰响应被分离开来,使系统既有较好的设定值响应性能,又有较好的抗干扰性能和鲁棒性能。内模控制(IMC)结构的最大优点是把伺服问题与鲁棒及抗干扰性问题分开处理、使分析、设计和调整都大为简化,同时又能像Smith预估器那样适用于大时滞系统。
在现实中,PID控制存在的主要问题有:一是控制器适应系统不确定性的能力不够强,难以适应较大范围的不确定性;二是在不确定性范围内,系统性能没有得到综合考虑,一致性差。而IMC只需调整滤波器参数,就可影响系统的动态指标并得到所需的系统鲁棒性。从而使滤波器参数与系统控制质量之间建立起简捷的对应关系。
4 结语
本文分析研究了工业过程中的控制策略,对分散预测控制进行了详细的叙述,提出了一种基于纳什最优的多时标控制算法,另外对内模控制技术进行了介绍。今后的研究工作主要在以下几方面深入:
4.1 对智能控制尤其是粗糙控制理论进行深入研究
4.2 进一步提高多时标分散预测控制算法的鲁棒性、可靠性、实时性
4.3 深入研究各种先进控制技术,并进行适当结合,进一步提高工业控制的效率和质量
[1]谢克明,侯宏仑.复杂系统的智能控制算法[J].太原理工大学学报,1998,29(6):568.
[2]Gao Zhipiang, Thomas A.Trautzsch,James Sauson.A stable self-tuning fuzzy logic control system for industrial temperature control problems[A]//IEEE Industrial Application Society 2000 Annual Meeting and World Conference on Industrial Applications of Electricial Energy[C].USA:Cleveland,2000.
[3]Astrom K J,Hang C C,Persson P,et al.Towards intelligent PID control[J].Automatica,1992,28(1):1-9.
[4]钱积新,赵均,徐祖华.预测控制[M].北京:化学工业出版社,2007.
[5]马志锋,刑汉承,郑晓妹.粗糙控制中的规则获取策略研究[J].工业仪表及自动化装置 2000,6:58-61.
[6]D E Rivera,M Morari,and S Skogestad.Internal model control:4.PID controller design[J].Ind.Eng.Chem.Pro.Des.Dev.,1986,25:252-265.
[7]Wang Lihui, Sivaram Balasubramanian,et al.Agent-based intelligent control system design for realtime distributed manufacturing environments[A]//Agent-based Manufacturing Worksshop Autonomous A-gents’98[C].Minneapolis/Stpaul:University of Calgary,1998.
[8]王树青.先进控制技术及应用[D].2001:11-14.
[9]佟绍成.非线性系统的自适应模糊控[M].北京:科学出版社,2006.
