基于车头时距交通信号的模糊控制系统的研究

罗全恒，李佳奇

（河西学院 物理与机电工程学院，甘肃 张掖734000）

随着我国经济的持续发展，城市化进程不断加快，机动车辆快速增加，使得交通出行量不断增长，城市交通供给严重不足。在这种情况下，为了提高城市道路的通行能力，减少交叉路口对车辆的延误，人们开始研究智能交通系统ITS(Intelligent Transportation System)。模糊控制是一种不需要建立被控对象精确的数学模型的一种智能控制，它是基于一种规则的控制，采用的是语言型控制规则[1-2]，因而控制规则和控制机理容易被人们理解和接纳。

自从PAPPIS[3]等人将模糊逻辑[4]应用于城市交叉路口信号控制中以来，国内外许多学者也进行了这方面的研究工作。尽管后续也有很多人研究了双向车流和多相位的模糊控制系统，但是主要以当前绿灯相位的车辆排队长度和红灯相位的车辆排队长度为模糊控制器[5]的输入变量，以绿灯相位的绿灯延时为模糊输出，很少考虑车头时距[6]这个重要参数。本文将车头时距作为实现绿灯时间修正的模糊控制器输入变量之一来提高绿信比，充分利用绿灯时间，从而提高通行能力。

1 系统模型

本文研究的是八车道十字路口，有机动车道和非机动车道，机动车道用到的交通数据来自各个车道的检测器，每一车道有两个检测器，一个设在停车线处，称为前端检测器，用于检测该车道的车辆离开数；另一个设在距停车线一定距离处，称为后端检测器，用于检测车辆到达数，根据检测算法可以得到某车道上两检测器之间的排队车辆数。所需考虑的车流有东西直行、东西左行、东西右行、南北直行、南北左行和南北右行共6个相位[7-9]，交通信号控制就是决定一个周期内的相位如何变化以及每个相位应该分配多少时间，所以为了控制交叉口的交通信号，首先要选择组成周期的相位。在自行车和行人流量不大的交叉口，将其合并专用相位，这时采用汽车右行和自行车分时复用一个信号相位的办法。

2 系统模糊控制算法

模糊控制模拟了人脑的思维、推理、决策的过程，所以交叉口交通信号的控制就是模仿有经验的交警指挥过程。根据其指挥过程，设计了系统模糊控制的总体规划方案，图1所示即为该方案算法的组成框图。

第一级为观测级；第二级为决策级。观测级包括两个模块：红灯相位选择模块和绿灯相位观察模块。决策级也包含两个模块：初级决策模块和总决策模块。每个模块都是一个子模糊控制器。

算法描述如下：红灯相位选择模块根据车辆检测器检测到的交通信息判断出当前绿灯方向外所有红灯相位的交通状况，计算各红灯相位等待绿灯的紧迫度，并确定出对绿灯要求最为紧迫的红灯相位作为下一个绿灯相位的候选相位和它的相位紧迫度，将它们传送给初级决策模块；绿灯相位观察模块根据车辆检测器检测到的交通信息判断出当前绿灯方向交通状况，确定绿灯相位繁忙度,也将其传送给初级决策模块；初级决策模块红灯相位等待绿灯的紧迫度和绿灯相位的繁忙度,决定是切换相位还是延长当前绿灯时间。如果是延长该相位绿灯时间，则将该相位绿灯的繁忙度传送给绿灯时间修正模块，该模块根据繁忙度和该相位的车头时距得出修正时间，从而得到了绿相位总的绿灯时间；如果由红灯相位选择模块选出的相位紧迫度比由绿灯相位观察模块观察的绿灯相位繁忙度高,则初级决策模块立刻进行绿灯相位的切换，这样就不需要绿灯时间的修正。

3 模糊控制器的设计

模糊控制器的设计包括两大部分：第一级的观测子系统设计和第二级决策子系统的设计。

3.1 绿灯相位观察模块

绿灯相位观察模块以绿灯相位交通流数据作为输入，以产生的绿灯相位繁忙度Bt作为输出。绿灯交通流数据选择绿灯相位剩余车辆数qg和绿灯相位经过最小绿灯时间后的绿灯延长时间tg。

(1)数据处理与输入输出变量的确定

qg=max(qg1，qg2)，式中，qg1和 qg2分别为绿灯相位两个车流停留在车道上两检测器之间的车辆数。

(2)模糊推理关系

3.2 决策级子系统设计

3.2.1 初级决策模块

初级决策模块的输入是候选相位Pr、相位紧迫度Up和繁忙度Bt，输出是决策程度 Dc。Pr是由红灯相位选择模块选出的相位，Up是此相位的相位紧迫度，Bt是绿灯相位观测模块输出的绿灯相位繁忙度。Dc决定是否将通行权付给候选相位Pr。

(1)模糊推理关系

(2)模糊规则的确定[10-11]与Matlab实现

通过总结实践和专家经验，建立了模糊控制规则，原则是：如果候选相位的紧迫度高或当前绿灯相位的繁忙度低，那么这个模块将停止当前绿灯相位并给候选相位一个绿灯信号。利用Matlab工具箱中Viewsurf菜单命令可以看到模糊控制规则曲面图。

3.2.2绿灯相位时间修正量模块

(1)模糊输入输出变量

输入变量：绿灯延长持续时间ET和车头时距GAP，ET 和 GAP 的模糊语言是：ET={短，中等，长}，GAP={小，中等，大}。

(2)绿灯持续时间ET、车头时距GAP以及修正时间的赋值表分别如表1～表3所示。

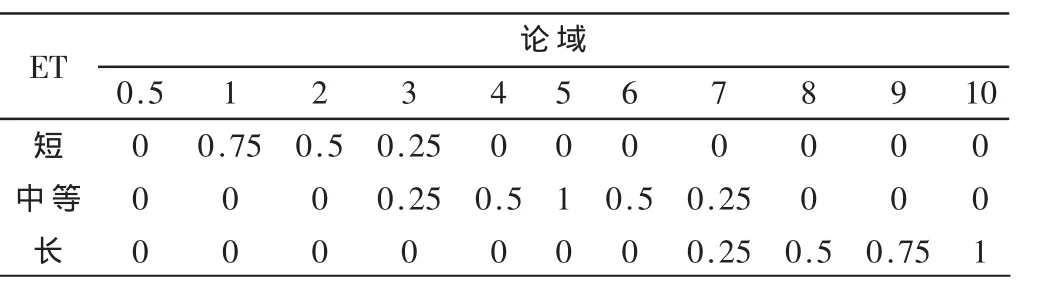
表1 ET的赋值表

(3)模糊规则的确定与Matlab的实现

模糊规则的确定依据:绿灯持续时间长或车头时距大，则修正时间就长。同样利用Matlab工具箱中Viewsurf菜单命令可以看到模糊控制规则曲面图。

表2 车头时距的赋值表

表3 修正时间的赋值表

4 仿真结果及其分析

本文以张掖市盘旋路十字路口为研究对象，利用Matlab软件进行编程仿真，实际测量各个交叉口的交通数据，对一段时间数据进行统计分析，根据分析结果生成车辆数。对于六相位（i=6），每个相位有两股车流（j=2）的典型交叉口，T时间内交叉口的每辆车的平均延误时间可用下式表示[12]：

式中，λ为绿信比，C为信号周期，x为相位饱和度，q为车辆到达量，y为流量比率(q/s)。仿真中采用的饱和流量 Sij全部取 2 000 veh·h-1。仿真时间按1 h计算，程序自动计算各方向的车辆到达率和平均延误时间，从而考察采用不同控制策略时的交叉口的总体运行效率，仿真结果如图2所示。

图中的*曲线表示模糊控制系统的控制方案仿真图，+曲线表示基于车头时距的模糊控制系统的控制方案仿真图。经仿真结果数据分析，在交通流低峰期，即0＜λ＜0.1时，基于车头时距模糊控制系统相比没有基于车头时距的模糊控制系统平均车辆延误减少了43.561%；在交通流中峰期，即 0.1＜λ＜0.3时，前者比后者减少了 32.658%，在交通流高峰期，即 0.3＜λ＜0.4时，前者比后者减少了11.125%。这说明了在交通流不是高峰的前提下，前者比后者控制效果要好得多，大大减少了平均车辆的延误时间，提高了交叉口的通行能力。

利用自动化手段和技术，实现车辆智能、道路智能必将形成新的智能交通控制系统。模糊控制是一种智能控制,由于其内部并不含有最优控制算法，所以不能针对某一性能指标给出最优解。因此需要改进模糊控制算法,提高模糊控制的精度。本文在自适应模糊控制的基础上增加了绿灯时间修正模糊算法,即基于车头时距对绿灯时间进行了微调，对模糊控制精度方面作了有益的尝试。仿真结果表明,该算法易实现且效果好。

[1]汪培庄.模糊集合论及其应用[M].上海：上海科技出版社，1983.

[2]冯冬青，谢宋和.模糊智能控制[M].北京：化学工业出版社，1998.

[3]PAPPIS C P，MAMDANI E H.A fuzzy logic controler for a traffic junction[J].IEEE Trans on SMC，1997，7(10)：707-717.

[4]褚静.模糊控制原理及应用[M].北京：机械工业出版社，2005.

[5]华宝玉，何迪.交叉口信号协调控制适用性仿真研究[J].铁路计算机应用，2007，16(7)：12-15.

[6]陈光勤.基于车头时距的快速公交车辆交叉口信号优先[J].交通与计算机，2005，23(3)：11-15.

[7]LEE J H，KWANG H L.Distributed and cooperative fuzzy controllers for traffic intersections Group[J].IEEE Transactions on System，Man and Cybernetics，1999(29)：263-271.

[8]陆化普，李瑞敏.智能交通系统概论[M].北京：中国铁道出版社，2004.

[9]交通部公路科学研究所.中国智能交通系统体系框架研究总报告[R].北京：交通部公路科学研究院，2001.

[10]CHIU S.Adaptive traffic signal control using Fuzzy logic[C].Proceedings of the IEEE Ingelligent Vehicles Symposium.1992：98-107.

[11]OSTERGARAD J J.Fuzzy logic control of a heat exchange process[J].in Fuzzy AUtomata and Decision Processes.Amsterdam：Gupta MM.Et.Eds.NorthHolland，1997(3)：48-65.

[12]王长军，卢静.基于思维过程的单交叉路口多相位模糊控制算法研究[J].城市交通，2004，2(3)：14-16.