过程强化装置中双偏心转子的运动分析

朱瑞林，朱国林

(1.湖南师范大学工学院，长沙 410081;2.江西警察学院，南昌 330103)

1 前言

笔者曾在文献[1] 中介绍了一种制取生物柴油的过程强化装置，这种装置利用双偏心转子推动活塞作往复运动使反应器内的物料产生振荡以强化反应过程。研究发现，偏心转子其实只是其几何圆心作简谐振动(正/余弦运动)，某些情况下并不能保证由转子驱动的活塞作同样的简谐振动[2]，而一些机械类文献[3～9]并未对此予以分析研究。研究还发现，当活塞不能作简谐振动时，若使用双偏心转子，则左(右)活塞上升(下降)的距离不等于右(左)活塞下降(上升)的距离，因而两活塞内端面间的距离不能保持恒定，这对反应器内的介质压力会产生一定影响[2，10，11]，而对于这些问题也未发现相关研究。对凸轮(偏心轮)的研究不少，如 Chiara Lanni[12]等研究了三段式圆弧凸轮的解析设计，提出了凸轮轮廓的解析公式，并与尺寸参数进行了关联，其中也未涉及本文要研究的问题。因此研究这种双转子结构的运动特点并探讨解决上述问题的方法是必要的。本文在研究这种双转子机构的运动特点的基础上，探讨反应器在两活塞内端面之间的空间长度和位置以及活塞的行程与速度的计算公式和方法，并提出使活塞作与转子圆心同样的简谐振动的措施，以保持两活塞内端面之间的长度在两活塞运行过程中恒定不变，从而消除对反应器内介质压力的影响，这对一些处理流体介质的设备很有意义。

2 运动分析

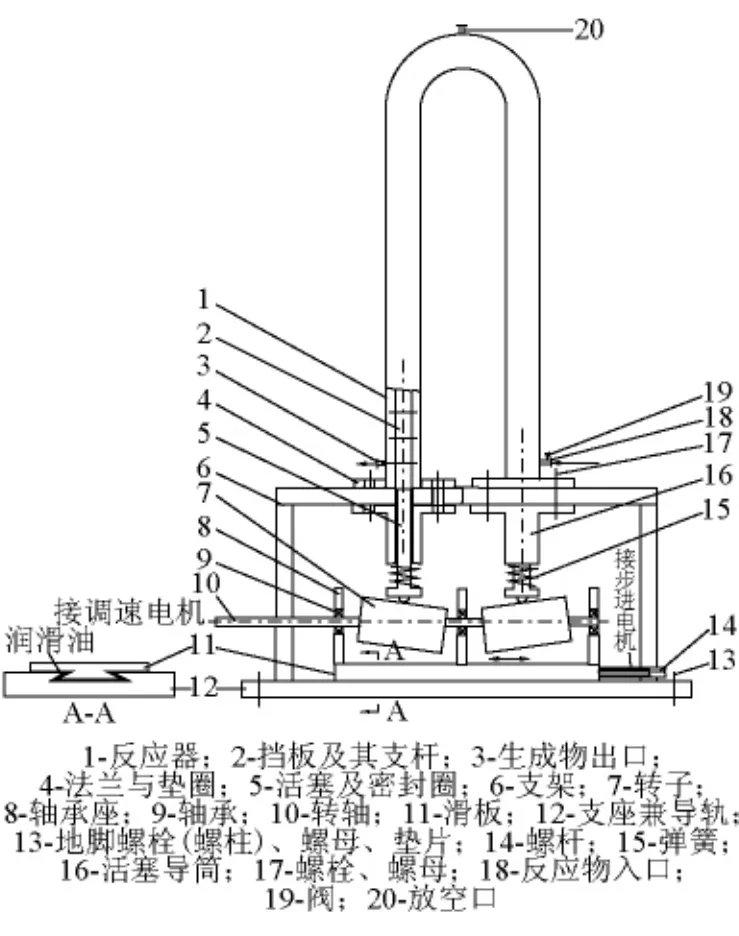
图1 过程强化装置Fig.1 A rig of process intensification

图1即为文献[1] 中的过程强化装置，为便于分析，将涉及双偏心转子的局部放大，如图2所示，这是对称安装于同一转轴上的偏心圆柱转子和由转子推动的活塞。转子转轴与其几何中心线有一夹角α，使得当活塞不处于转轴与转子几何中心线的交点o″上方时，转子有一偏心距e，可推动活塞作往复运动而完成某种生产过程。转子还能沿其旋转轴方向移动，以便改变e的大小，即改变活塞振幅。转子对称安装，即左、右转子的水平倾角相同而方向相反，活塞运行过程中，其内端面的最高位置为+e，即左活塞内端面最高能达到图2的m－m截面，右活塞内端面最高能达到m'－m'截面，m－m与m'－m'截面在同一高度;活塞内端面的最低位置为－e，即左活塞内端面最低能达到n－n截面，右活塞内端面最低能达到n'－n'截面，n－n与n'－n'截面在同一高度;因此活塞的总行程距离为2 e，振幅为e;平衡位置时活塞的行程距离为0，见图2的o－o截面和o'－o'截面，o－o和o'－o'截面在同一高度。显然，当转子以角速度ω旋转时，转子几何截面中心a在铅垂方向的行程为ecosβ，即简谐振动，其中β为转子旋转到任意位置时转子几何截面中心a和旋转中心b的连线(连线长度即为偏心距e)与铅垂方向的夹角，β=ωt，t为时间，见图3，图中 L代表左转子，R代表右转子(下同)。下面的运动分析可以证明，对于图2活塞外端与转子点接触的结构，虽然转子对称安装，但左、右活塞的往复运动并非严格对称，即左活塞内端面上升的距离并非时刻等于右活塞内端面下降的距离，亦即左、右活塞内端面在任何时刻或任何位置角度β处的行程并非均为简谐振动规律ecosβ 和 －ecosβ(或 － ecosβ 和 ecosβ)，而是左(右)活塞上升的距离略小于右(左)活塞下降的距离，从而使两活塞内端面之间的长度略有增大。要消除此种现象而保证左、右活塞内端面在任何时刻或任何β处的行程均为简谐振动规律ecosβ和－ecosβ(或－ecosβ和ecosβ)，从而维持设备空间大小不变，只需将活塞外端与转子的点接触方式改变为线接触方式，即在活塞外端加一接触件即可。

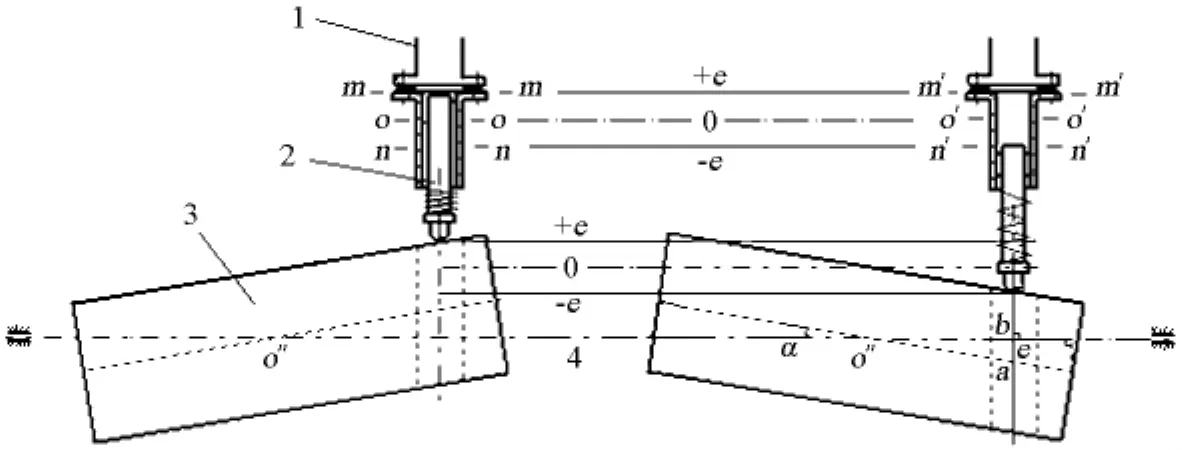
图2 同轴对称安装的点接触式圆柱转子机构Fig.2 A mechanism constructed of cylindrical cams mounted on identical shaft and touched with pistonns by points

图3 转子几何中心在铅垂方向的简谐运动Fig.3 Simple harmonic motion of geometric center of the cams in vertical direction

2.1 活塞外端与转子点接触

所谓点接触，即活塞杆外端直接以尖顶与转子接触。不失一般性，可设初始时刻左活塞在最高位置，右活塞在最低位置。图4为左转子从使活塞处于最高位置旋转到使活塞处于最低位置的横截面(图4的4个图中，从左到右是左转子从使活塞处最高位置旋转到使活塞处最低位置过程中4个不同时刻的位置，下同)，这一过程中左转子旋转一周;图5为相应时刻右转子从使活塞处于最低位置旋转到使活塞处于最高位置的横截面(图5的4个图中，从右到左是右转子从使活塞处最低位置旋转到使活塞处最高位置过程中4个不同时刻的位置，下同)，这一过程中右转子旋转一周。图4、图5均是从转轴的右端往左端看转子，假设转子(轴)顺时针方向旋转(左、右转子转向一样)。

先讨论左转子的运动。参阅图4，当转子旋转到任何位置角度β时，依几何关系有

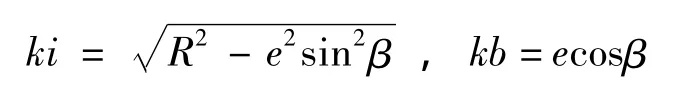
接触点i到回转中心b的距离

i到0－0的距离即为活塞内端面的行程:

可见，左活塞内端面在某时刻或某位置角度β处的行程并非ecosβ，而是如式(1)所示。其中为附加项，与e和R均有关;ecosβ为简谐振动行程，仅与e有关，与R无关。

为便于分析，令

以上各式中，e为转子偏心距;ω为转子角速度;R为转子半径;β(其中β=ωt)为转子位置角度，对左转子β以活塞处于最高位置时为起始位置(β=0)，t为时间;对右转子β以活塞处于最低位置时为起始位置(β=0)。从转轴4的右端往左端看转子，设左、右转子均顺时针方向旋转。

λ－λ=e/R

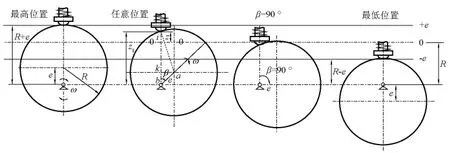
图4 左转子从使活塞处于最高位置旋转到使活塞处于最低位置(从左到右)Fig.4 A procedure that the left cam drives the piston to move from the highest to lowest position(from the left to the right)

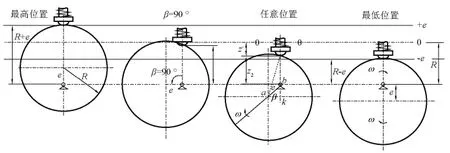
图5 右转子从使活塞处于最低位置旋转到使活塞处于最高位置(从右到左)Fig.5 A procedure that the right cam drives the piston to move from the lowest to highest position(from the right to the left)

右转子的运动分析如下。由图5可知

由于在初始时刻左转子处于最高位置，右转子处于最低位置，所以右转子旋转角度β的起始位置如图5所示。接触点i到回转中心b的距离

接触点到0－0的距离 -z′=R-z2⇒z′=z2-R

联系式(1)可知，右活塞上升或下降的距离不等于左活塞下降或上升的距离。令左、右活塞行程之和

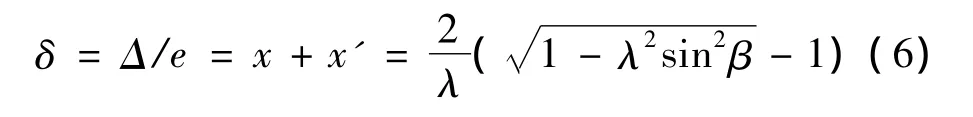
一些λ下任一瞬间β处的δ如图7所示，δ也是受λ的影响的，λ越大，δ越大。要改变δ的大小，只需调节λ即可。以R=80 mm为例，设λ=0.5，于是 e= λR=40 mm，β =90 °处 Δ = δe=－0.5359×40= －21.4 mm，又设设备长度 L=1000 mm，Δ/L=21.4/2000=2.14%。

根据sin(180°－β)=sinβ和 cos(180°－β)=－ cosβ，比较式(2)与式(4)可知 x'|β=x|180－β。

λ =0.5时任一时刻左、右活塞的 x、x'及 δ(其中δ=x+x')见图8。可见x≠－x'，即由于两活塞均不以纯简谐振动规律运动(但仍为以2为周期的往复运动)，任一时刻二者的位移并不抵消。此图也可用于查取任意时刻活塞的行程。

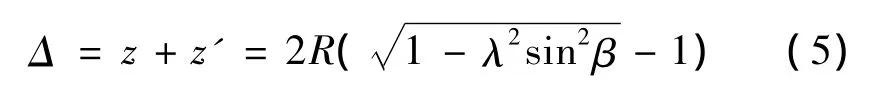
若右活塞上升或下降的距离等于左活塞下降或上升的距离，则Δ应为0，所以Δ实际上也是任一时刻不同λ下两活塞内端面间的距离变化。显然Δ并不恒为0，这表示当转子与活塞点接触时，由于左、右转子并不各自以简谐振动规律运行，故二者的位移并不完全对称。由式(5)可知，Δ＜0，这表示对图1所示的结构，机构运行过程中两活塞内端面间的距离始终略呈增大状态，不会引起设备内介质压力的增加但会引起设备内介质压力的减小，适用于设备空间需要有增大的场合或空间的增大影响不大的场合;对不允许设备内压力减小的场合会有影响。若要使运行过程中两活塞内端面间的距离呈缩小状态，只需相应地改变转子截面的几何形状。式(5)还表明，Δ以90°为对称，并在β=90°处为最大值(负的)，以180°为周期，当 β=k×180°时(k为整数)，Δ=0，即仅在这些时刻，左(右)活塞上升(下降)的距离等于右(左)活塞下降(上升)的距离，两活塞内端面间的距离为平衡位置时的距离。令

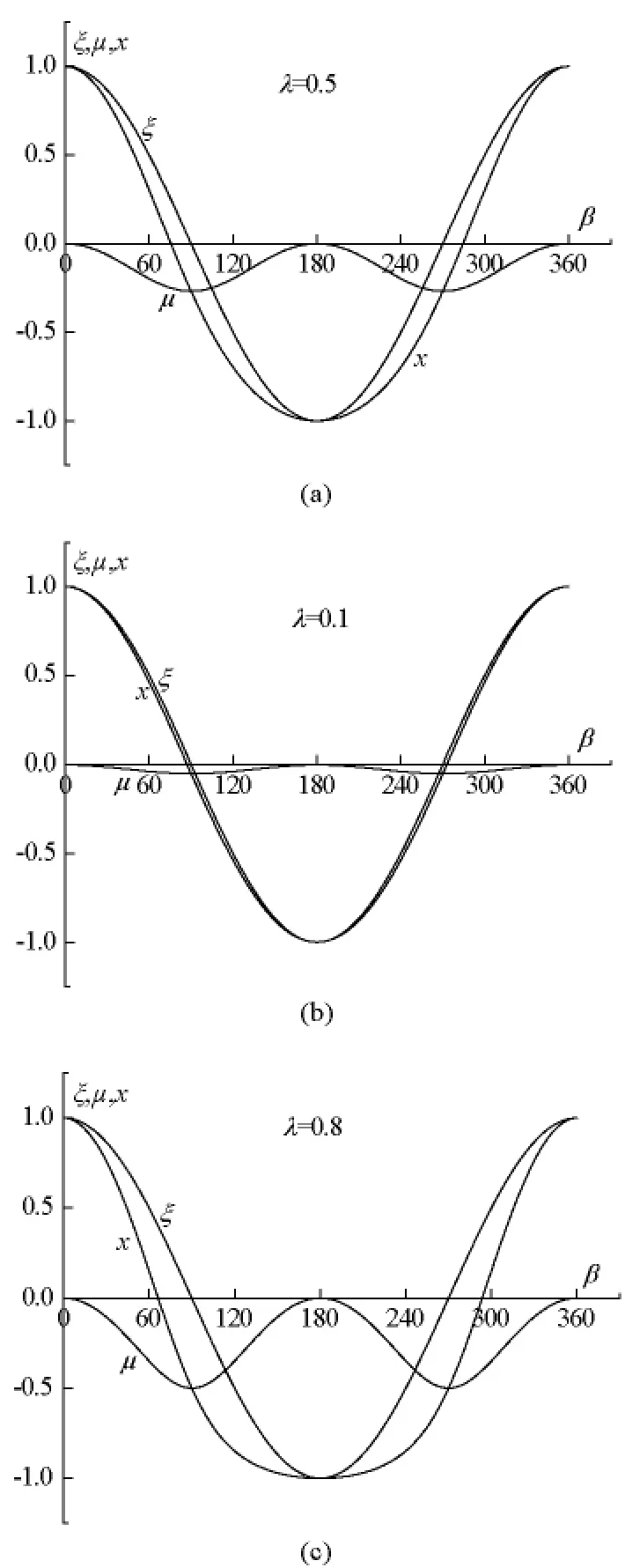
图6 任意时刻不同λ下的ξ、μ、xFig.6 ξ，μ，x at arbitrary time and various λ

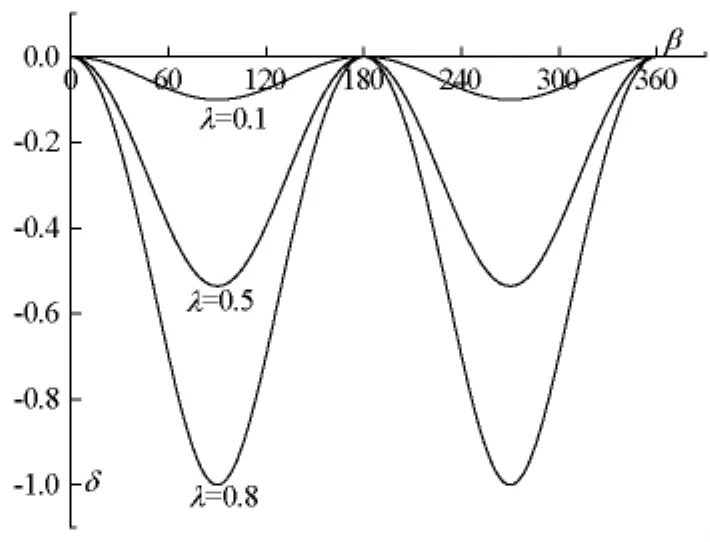
图7 任意时刻不同λ下两活塞内端面间的距离变化Fig.7 Variations of distance between inside end faces of the two pistons at arbitrary time and various λ

图8 任意时刻不同λ下左、右活塞行程比较及间距变化Fig.8 Comparison of the two pistons’travels and variations of distance between inside end faces of the two pistons at arbitrary time and various λ

2.2 消除两活塞内端面间距变化的措施

在某些情况下需设备操作空间长度保持不变，即δ=0，亦即保持两活塞内端面间的距离在机构运行过程中始终等于图1中设备从o－o至o'－o'截面间的长度，以使设备1内的介质压力保持不变。而以上已证明，转子与活塞外端点接触时达不到此目的。由以上对点接触的分析可知:在活塞外端装设一个与活塞轴线垂直的接触件6，使接触件与转子横截面成切线接触，就能使左右活塞的运动都为简谐运动，从而使δ=0，如图9、图10所示，现证明如下。

图9 切线接触时左转子从使活塞处于最高位置旋转到使其处于最低位置(图中6为接触件)Fig.9 A procedure that the left cam drives the piston to move from the highest to lowest position when the piston touches the cam by a tangent line(No.6 is a touch element)

图10 切线接触时右转子从使活塞处于最低位置旋转到使其处于最高位置Fig.10 A procedure that the right cam drives the piston to move from the lowest to highest position when the piston touches the cam by a tangent line

对左转子有kb=ecosβ z1=R+ecosβ

接触线至平衡位置0－0的距离为

对右转子有kb=ecosβ z2=R－ecosβ

接触线至平衡位置0－0的距离为

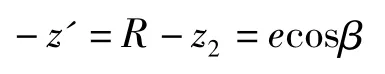
即

可见当活塞外端与转子切线接触时，左、右转子的运动都为简谐运动，是完全对称的，两活塞间的长度在活塞运动过程中将恒定不变。

3 原因分析

以上已证明，转子与活塞外端点接触时，左、右活塞并不以简谐振动规律运行，二者的位移不完全对称，即左(右)活塞下降(上升)的距离不等于右(左)活塞上升(下降)的距离。之所以发生这种情况是由于几何误差引起的。参见图11，转子与活塞外端点接触时，左活塞外端所处的高度为e－e，而转子与活塞线接触时，左活塞外端所处的高度为f－f，f－f是转子横截面最高点处的切线，如同接触件与转子接触一样。由几何分析容易推出e－e与f－f位置之差正是同理，转子与活塞点接触时，右活塞外端所处的高度为d－d，而转子与活塞切线接触时，右活塞外端所处高度为c－c，c－c是转子横截面最高点处的切线，如同接触件与转子接触一样。由几何分析容易推出c－c与d－d位置之差也正是-R。由图11可见，Δ/2是左活塞点接触情况下比切线接触情况下从最高点多下降的距离，也是右活塞点接触时比切线接触时从最低点少上升的距离，二者之和正是设备空间长度的增加值 Δ =若在转子运行过程中左、右活塞外端均到达转子横截面最高点处的切线位置，即如切线接触的情况一样，则左、右活塞必以简谐振动运行，从而保持两活塞内端面间的距离不变。图12进一步说明了点接触与切线接触的差别，图中虚线为切线接触情况。

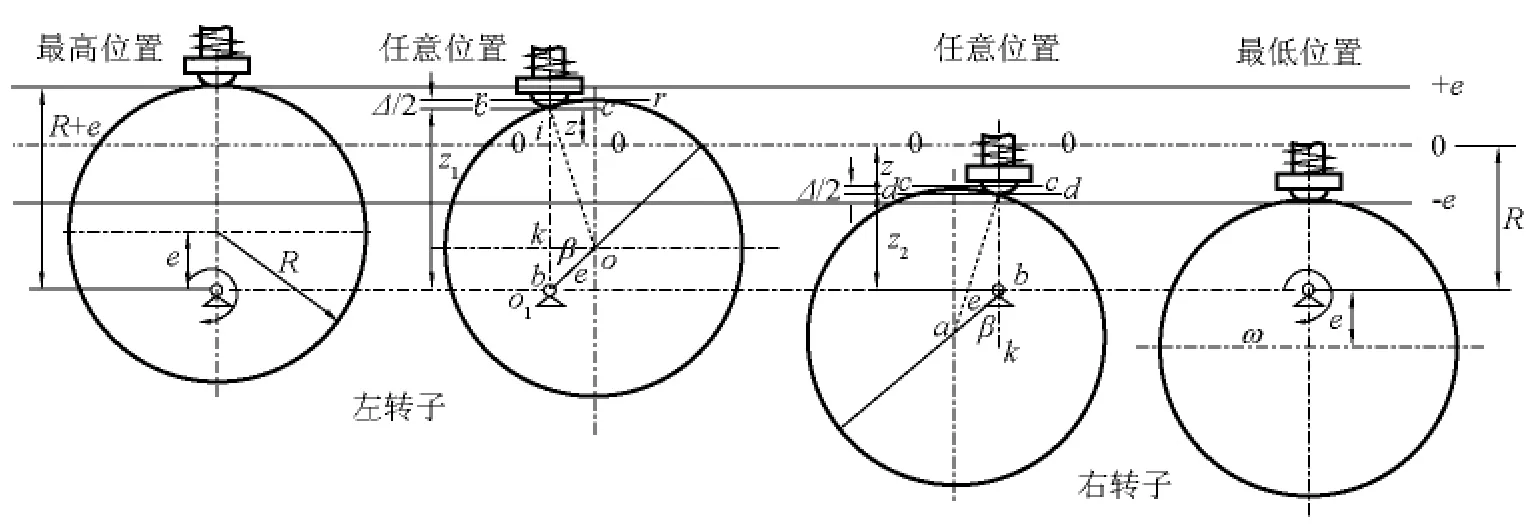
图11 转子与活塞外端点接触时，左、右活塞的运动不完全对称的原因分析图Fig.11 A figure to analyse the causes that the two pistons do not move completely symmetrically when the piston touches the cam by a point

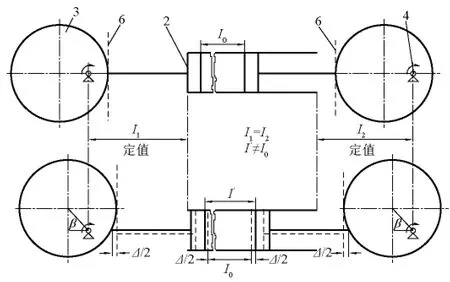
图12 点接触与切线接触的差别(虚线为切线接触情况)Fig.12 Difference between point and tangent line touch(dash lines represent the case of tangent line touch)

4 结语

本文导出的转子运动的解析解(理论解)为转子的运动规律提供了清晰的运动图景，所发现的点接触情况下由转子驱动的活塞并非简谐运动(即纯正/余弦运动)，是现有技术或理论所忽略的一个理论问题。此外，工业上许多设备(特别是过程设备)内的介质压力除工艺要求的变化外，不允许有因设备的运转过程而发生的压力波动。本文提出的确保由转子驱动的活塞作简谐运动从而解决因设备的运转过程而发生压力波动的措施在工程上有一定意义，因为不许可的压力波动会影响生产的正常进行，这种影响有时是很严重的，不解决会严重影响生产;同时这一措施对于机构分析也有一定参考意义。

[1] 朱瑞林，朱国林.过程强化技术及其装置制取生物柴油初探[J] .中国工程科学，2010，12(9):46－51.

[2] 朱瑞林.一种工艺过程流体强化装置[J] .石油化工设备，2006，35(1):68 －71.

[3] Robert L Norton.Design of Machinery An Introduction to the Synthesis and Analysis of Mechanisms and Machines[M] . New York:The McGraw-Hill Companies，Inc.，2001.

[4] John J Uicker，Gordon R Pennock，Joseph E Shigley.Theory of Machines and Mechanisms[M] .New York:Oxford University Press，2003.

[5] 费罗洛夫Κ Β.机械原理[M] .刘作毅译.北京:高等教育出版社，1997.

[6] 西北工业大学机械原理及机械零件教研室.机械设计(上、下册)[M] .北京:人民教育出版社，1980.

[7] 濮良贵，纪名刚.机械设计[M] .6版.北京:高等教育出版社，1996.

[8] 孙 桓，李继庆.机械原理[M] .西安:西北工业大学出版社，2003.

[9] 沈世德，徐学忠.机械原理[M] .2版.北京:机械工业出版社，2009.

[10] 蒋丽芬.化工原理[M] .北京:高等教育出版社，2007.

[11] 谭天恩，窦 梅，周明华.化工原理[M] .北京:化学工业出版社，2006.

[12] Chiara Lanni，Marco Ceccarelli，Giorgio Figliolini.An analytical design for three circular-arc cams[J] .Mechanisms and Machine Theory，2002，37:915 －924.