Thermodynamics-inspired inverse halftoning via multiple halftone images

SAIKA Yohei，AOKI Toshizumi

(1.Department of Information and Computer Engineering，Gunma National College of Technology，580 Toriba，Maebashi，371－8530，Japan;2.Department of Natural Science，Gunma National College of Technology，580 Toriba，Maebashi，371－8530，Japan)

Thermodynamics-inspired inverse halftoning via multiple halftone images

SAIKA Yohei1，AOKI Toshizumi2

(1.Department of Information and Computer Engineering，Gunma National College of Technology，580 Toriba，Maebashi，371－8530，Japan;2.Department of Natural Science，Gunma National College of Technology，580 Toriba，Maebashi，371－8530，Japan)

Based on an analogy between thermodynamics and Bayesian inference，inverse halftoning was formulated using multiple halftone images based on Bayesian inference using the maximizer of the posterior marginal(MPM)estimate.Applying Monte Carlo simulation to a set of snapshots of the Q－Ising model，it was demonstrated that optimal performance is achieved around the Bayes－optimal condition within statistical uncertainty and that the performance of the Bayes－optimal solution is superior to that of the maximum－aposteriori(MAP)estimation which is a deterministic limit of the MPM estimate.These properties were qualitatively confirmed by the mean－field theory using an infinite－range model established in statistical mechanics.Additionally，a practical and useful method was constructed using the statistical mechanical iterative method via the Bethe approximation.Numerical simulations for a 256－grayscale standard image show that Bethe approximation works as good as the MPM estimation if the parameters are set appropriately.

inverse halftoning;statistical mechanics;Monte Carlo simulation;Bethe approximation;

1 Introduction

Researchers have long used Bayesian inference to investigate various issues in information science and technology such as problems related to image and signal processing［1－3］.During the last two to three decades，theoretical physicists［4］have studied such problems by using an analogy between statistical mechanics and the maximizer of the posterior marginal(MPM)estimate based on Bayesian inference.In the early stage of development in this field，physicists studied image restoration and error－correcting codes［4－5］to determine the feasibility of applying statistical mechanics to these problems.Researchers have since then applied statistical mechanics to various problems in information science and technology.

Researchers have been investigating digital halftoning print technology［6－7］for many years with the aim of generating a halftone image comprised of a set of black and white dots that are visually similar to the original image as seen by the human vision system.Many techniques，such as the organized dither method［6－7］，have been proposed for generating such image.The inverse of digital halftoning［8］，i.e.，“inverse halftoning，”is used to reconstruct the original image from the halftone image，and many techniques have been proposed fordoing this. Foran instance，Wong［9］proposed statistical techniques for a halftone image obtained using the error diffusion method.Then，Stevenson［10］applied maximum－a－posteriori(MAP)estimation to inverse halftoning of halftone images converted using either a dither method or an error diffusion method. Recently， Saika et al.［11］constructed a Bayes－optimal solution on the basis of the statistical mechanics of the Q－Ising model for the inverse halftoning problem.It uses the MPM estimate based on Bayesian inference.Other researchers have investigated super resolution，another typical problem in infor－mation science and technology.The objective is to construct a high－resolution image using multiple low－resolution images.Several researchers［12－13］have tried using Bayesian information processing from the statistical mechanical point of view.

In this study，a practical and useful method for inverse halftoning is proposed.It combines a statistical mechanical iterative method and a framework of super resolution to use multiple halftone images.This approach was adopted with the hope that statistical mechanics of Bayesian information processing would be available by using an analogy between statistical mechanics and the MPM estimate based on Bayesian inference.In particular，the statistical mechanical iterative method was used based on the Bethe approximation to approximate the MPM estimate established in the field of Bayesian information processing.Then，in order to realize inverse halftoning with high image quality，a framework of super resolution was also applied to multiple halftone images for inverse halftoning.Next，in order to clarify the performance of Bethe approximation from the theoretical point of view，the efficiency of the MPM estimate for inverse halftoning was examined using multiple halftone images based on Monte Carlo simulation for a set of snapshots of the Q－Ising model and the mean－field theory using the infinite－range model.First，Applying the Monte Carlo simulation to a set of snapshots of the 8－grayscale Q－Ising model，the statistical performance of the MPM estimate was clarified using 4 halftone images rewritten by the organized dither method based on the metric using the mean square error(MSE).The simulation showed that the optimal performance was achieved around the Bayes－optimal condition within statistical uncertainty and that the optimal performance is superior to that of the MAP estimation，which corresponds to the deterministic limit of the MPM estimate.These properties were qualitatively confirmed by analytical estimation based on the meanfield theory using the infinite－range model.On the other hand，from the practical point of view，the performance was investigated based on the Monte Carlo simulation for realistic images，i.e.，a 256－grayscale standard image“Lena”with 256 ×256 pixels.The simulation showed that the MPM estimate can reconstruct the original image using more than 36 halftone images，even if a uniform model prior is assumed.However，a fatal contour appeared in the images reconstructed using fewer than 16 halftone images.The contour can be removed by the MPM estimate using fewer than 16 halftone images if an appropriate model of the true prior which can enhance smooth structures is used.A practical and useful method was then developed for reconstructing images based on the Bethe approximation which approximates the MPM estimate.Simulation shows that Bethe approximation reconstructs the original image almost as good as Monte Carlo simulation and that only 11～15 iterations are needed to solve the self－consistent equations derived from the Bethe approximation.

The content of this paper is as follows.The general prescription of statistical mechanics and the analogy between statistical mechanics and Bayesian inference were briefly reviewed，describing the general formulation of inverse halftoning using multiple halftone images based on the statistical mechanics of the Q－Ising model.The performance of the present method was then examined.Monte Carlo simulation and analytical estimation were conducted based on the mean－field theorys，using the infinite－range model;its statistical performance for a set of snapshots of the Q－Ising model was estimated along with its performance for a realistic image.Finally，the performance of the presented statistical mechanical iterative method based on the Bethe approximation was estimated.

2 General formulation

2.1 statistical mechanics

As shown in Fig.1，a principal goal of statistical mechanics is to clarify thermodynamics of many－body systems starting with interactions between microscopic elements.In general prescription of statistical mechanics，thermal average of macroscopic physical quantity can be estimated as an ensemble average over all possible states using a probability distribution:

for a given HamiltonianH({S}).In this equation，a set of the Ising spin states{S}is used as a set of typical microscopic elements.The unit of temperature is taken such that Boltzmann’s constantkBis unified.As a result，β =1/T.Normalization factorZis called the“partition function”:

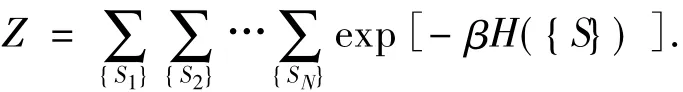
The probability distribution in Eq.(1)is termed the“Boltzmann factor”.Using the Gibbs－Boltzmann distribution，the thermal average of macroscopic quantityA({S})can be estimated as

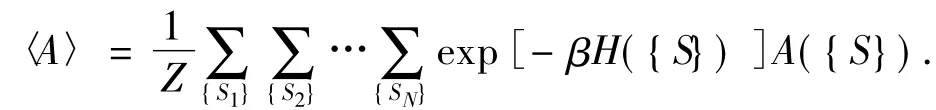
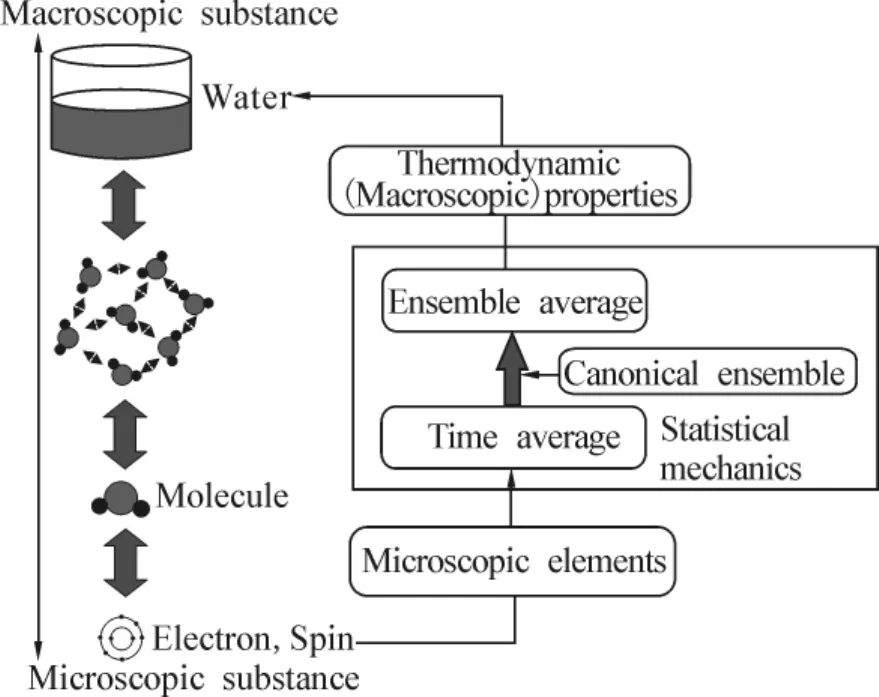
Fig.1 Main goal of statistical mechanics

Though it is difficult to calculate this macroscopic quantity directly，it can be estimated by using the approximation theories such as the mean－field theory and the Bethe approximation.As a recent development of statistical mechanics，researchers have clarified that statistical mechanics serves a framework and various techniques for probabilistic information processing based on the analogy(Fig.2)between statistical mechanics and Bayesian inference using the MPM estimate.

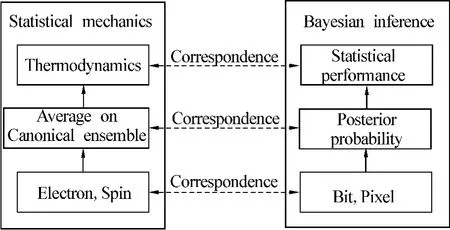
Fig.2 Analogy between statistical mechanics of physical system and Bayesian inference of information system

2.2 general formulation

Here，on the basis of the statistical mechanics of the Q－Ising model，the general formulation for inverse halftoning is shown using multiple halftone images based on Bayesian inference which is obtained through the MPM estimate.As shown in Fig.3，the framework is composed of two parts.One is the forward process corresponding to digital halftoning，and the other is the inverse process corresponding to inverse halftoning.

Fig.3 Framework of inverse halftoning via multiple halftone images

In the first step of the forward process，a set of original grayscale images was considered{ξx，y}，where ξx，y=0，1，…，Q－ 1 andx，y=1，2，…，L.These images were generated by the assumed true prior expressed as a probability distribution:

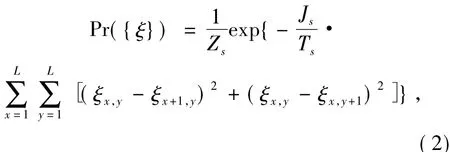
whereJsandTsare parameters for tuning“smoothness”in the pattern of the original image.Fig.4(a)shows a sample of the original image，i.e.，a snapshot of the 8－state Q－Ising model on a square lattice.Then，as shown in Fig.4(b)，a 256－grayscale standard image with 256 × 256 pixels，such as“Lena”，was used to investigate the performance for realistic images.

In the second step of the forward process，each original image{ ξx，y}is rewritten intop2kinds of halftone images{τx，y(m，n)}using the organized dither method and ap×pBayer threshold array{Mp}.Here，τx，y(m，n) =0，1，x，y=1，2，…，L，andm，n=1，2，…，p.Two example threshold arrays are shown in Figs.5(a)and(b).The threshold array{Mp}is given by

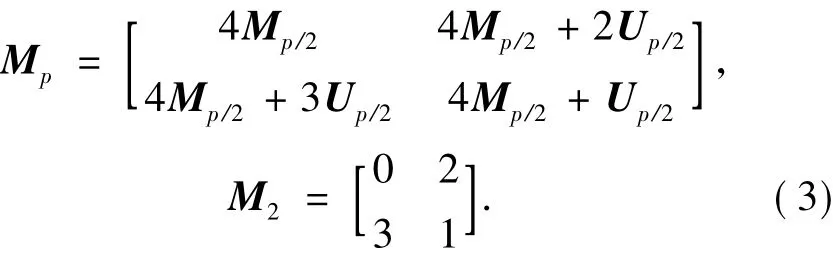
Fig.5 4×4 and 8×8 Bayer threshold arrays

Unis ann×nmatrix，the elements of which are unified.Threshold Mpis an integer from 0 top2－1.The halftone versions of the original images in Figs.4(a)and(b)are shown in Figs.3(c)and(d).When the original image{ ξx，y}is converted into the(m，n)－th halftone image{τx，y(m，n)}，a one－to－one correspondence between each pixel of the original image{ξx，y}and the threshold of the Bayer threshold array{Mp}is first created by making use of the correspondence:

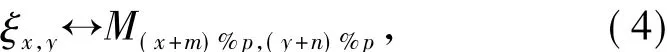
where(x+m)%pdenotes a surplus that divides(x+m)byp，and it is the same with(y+n)%p.Then，as shown in Fig.6，a threshold procedure is carried out for each pixel of the original image{ξx，y}by the corresponding threshold{Mp}:

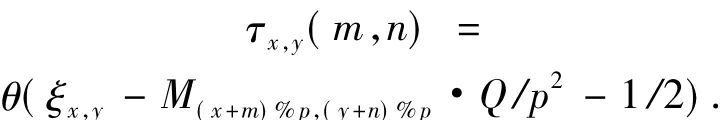
θ(·)is a unit－step function given by

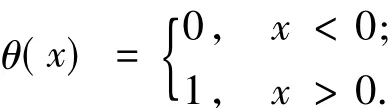
The halftone images in Figs.4(c)and(d)are visually similar to the original image as seen by the human vision system although information on the original image was lost through the halftone procedure.

In the inverse halftoning process，the original image is reconstructed so as to maximize the posterior marginal probability.The value of the(x，y)－th pixel in the reconstructed image is given by

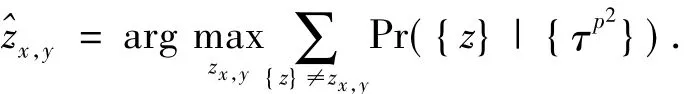
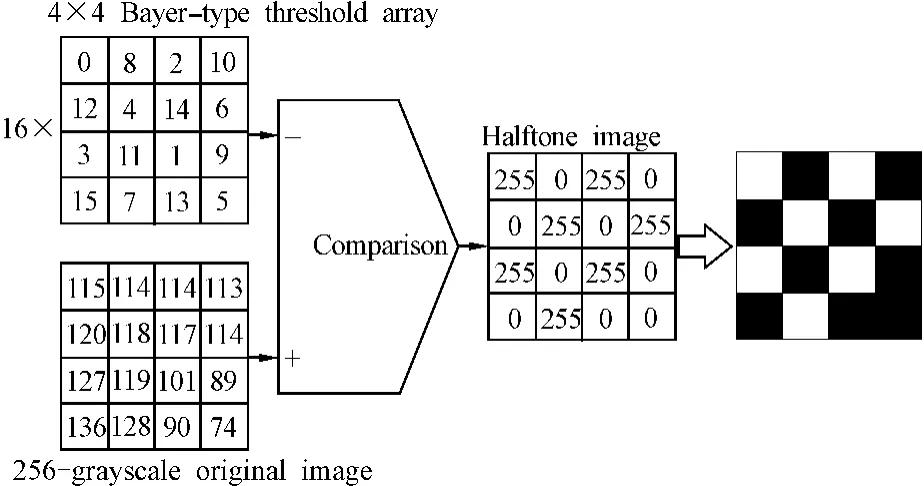
Fig.6 Digital halftoning using 4×4 Bayer-type threshold array

The posterior probability is estimated using the Bayes formula，

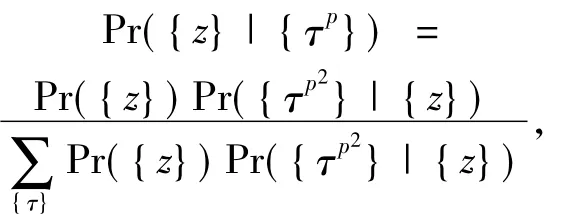
as well as the assumed model of the true prior along with the likelihood.The model of the true prior expressed by

is used so as to enhance smooth structures appearing in the pattern of reconstructed images.Furthermore，a model of the true prior is used，which is assumed to have the same form as the true prior in Eq.(2)so that an MPM estimate is constructed，including the Bayesoptimal solution.The likelihood that is expressed by the conditional probability representing the organized dither method via the Bayer threshold array is also used:

As seen from Fig.7，the likelihood has the property that the possible range of the gray－levelzx，ybecomes narrower at each pixel with the increase in the number of the halftone images.So，it is expected that the accuracy of the performance is improved with the increase in the number of the halftone images.

Fig.7 Range of grayscale restricted by the likelihood in Eq.(6)used for the present method

Then，the reconstructed image is obtained by

To estimate the performance of the present method，MSE was compared between the original and reconstructed images:

To estimate the statistical performance，MSE was averaged over the set of original images{ξx，y}:

3 Performance

3.1 Monte Carlo simulation

To quantitatively investigate the statistical performance of the present method，a set of the snapshots of the Q－Ising model was used on the square lattice.A set of the snapshots of the 8－grayscale Q－Ising model with 100 ×100 pixels(Fig.4(a))was used for the original images.The parameters in Eq.(2)were set toJs=Ts=1.Each original image was converted into four kinds of halftone images by the organized dither method using the 2 × 2 Bayer－type threshold array in Eqs.(3)and(4).Then，20 000 Monte Carlo steps were performed using the MPM estimate based on the Metropolis algorithm.

First，it was determined how MSE depends on parameterTmin Eq.(5)forJ=1.As shown in Fig.8，it is found that the performance of the present method is improved by introducing the model of the true prior and that the performance is optimal under the Bayesoptimal conditionTm=Ts=1 within statistical uncertainty.

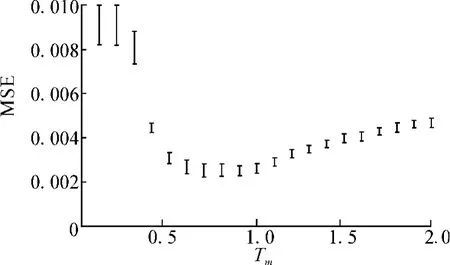
Fig.8 MSE as a function of Tmobtained by Monte Carlo simulation for a set of snapshots of Q-Ising model

These results suggest that the MPM estimate based on Bayesian inference works effectively for inverse halftoning by making use of the framework of the super resolution with multiple halftone images while the MPM estimate is improved by introducing the model of the true prior appropriately.

3.2 Mean-field theory

To qualitatively clarify the statistical performance of the MPM estimate based on Bayesian inference，the mean－field theory was tested using the infinite－range model，which was established in terms of statistical mechanics.These models seem to be very artificial in the sense that all pixels neighbor each other.However，the aim here is not to establish a model of practical usefulness but to understand generic features of macroscopic variables，such as MSE.

To use the mean－field theory for estimating the performance of the MPM estimate，the infinite－range versions of the model and true priors are first introduced:

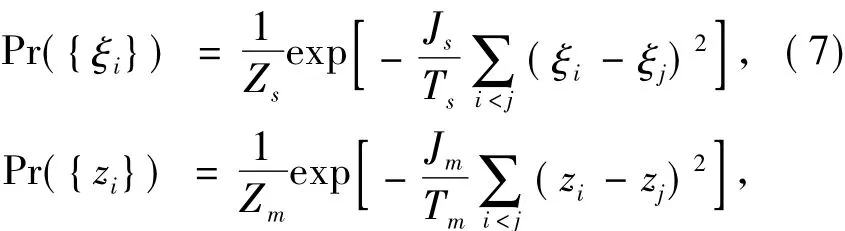
both of which are considered to approximate the assumed model and true priors in two dimensions.Following the strategy of the mean－field theory via the infinite－range model［4］，the configuration average of the partition function of the model system is then considered:

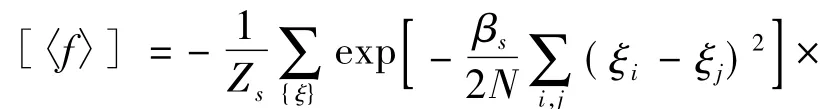
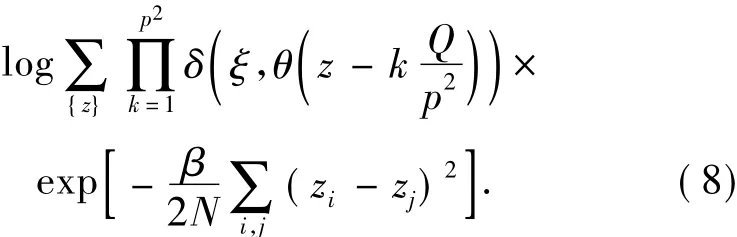
The summation in this equation applies to all over the lattice sites.Then，on the basis of the saddle－point conditions on the configuration average free－energy in Eq.(8)，self－consistent equations are derived onm0andm:

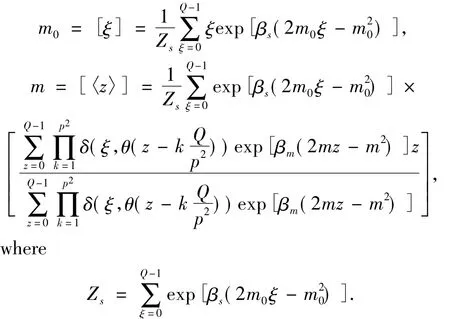
Here βs=1/Tsand βm=1/Tm.Using the solution to these self－consistent equations onm0andm，MSE averaged over the assumed true prior in Eq.(7)can be estimated from

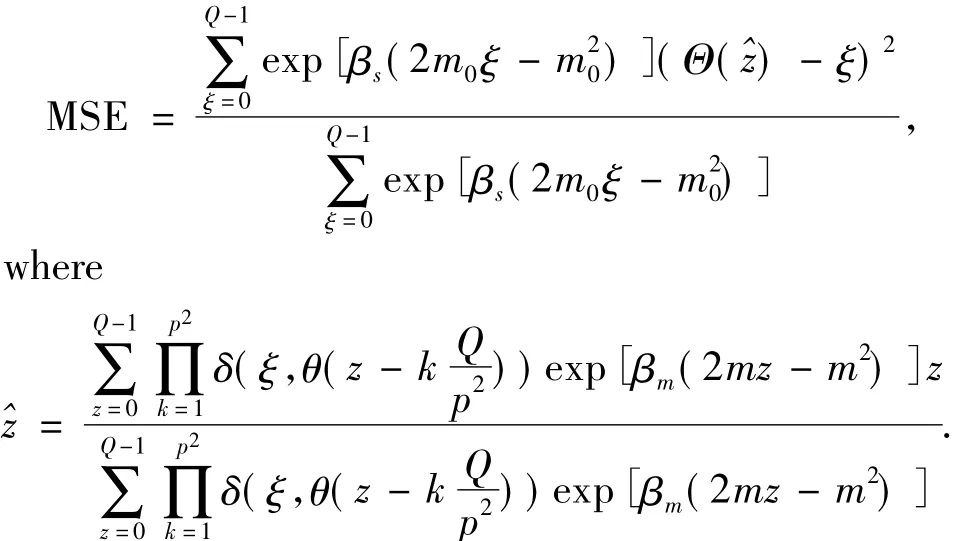
Using the solutions to the self－consistent equations onm0andm，MSE was analytically estimated without statistical uncertainty.

First，to clarify the performance of this model，it was estimated how MSE depends on parameterTm.As shown in Fig.9，it was found that the optimal performance is realized around the Bayes－optimal condition，that isTm=Ts，andJ=Js.These results indicate that the analytical estimate obtained using the infinite－range model qualitatively supports the results obtained using Monte Carlo simulation for the set of the snapshots of the Q－Ising model.It was found that MSE monotonically decreased with an increase in the number of halftone images and that perfect inverse halftoning was achieved withp2=Q.These results show that the analytical estimate qualitatively supports the results obtained using Monte Carlo simulation for a two－dimensional model.

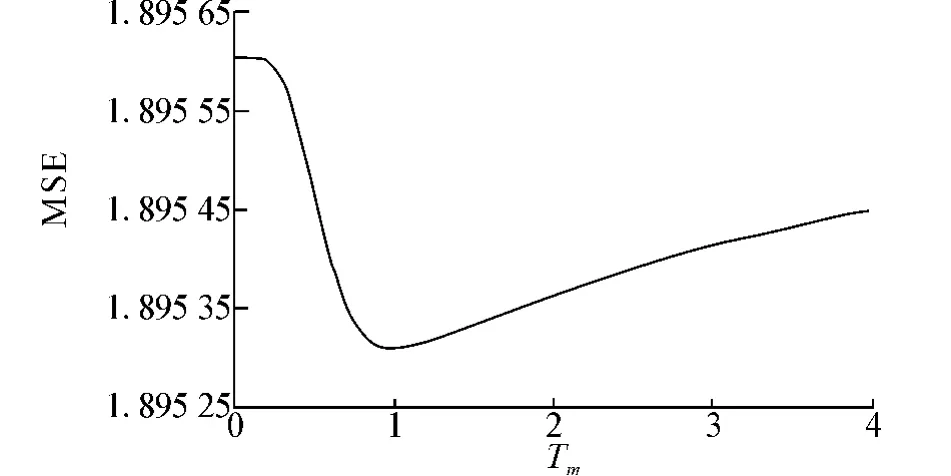
Fig.9 MSE as a function of Tmobtained by analytical estimate which was generated using infiniterange model

3.3 Realistic image performance

To investigate the performance of the MPM estimate for realistic images，Monte Carlo simulation was used to derive MSE for obtaining the standard“Lena”image(256－grayscale;256 × 256 pixels).Then，the performance of the MPM estimate was compared with those of other methods，such as the MAP estimation corresponding to theTm→0 limit of the MPM estimate and the conventional filter using a 3 ×3 Gaussian kernel.

First，the dependence of MSE on parameterTm，was investigated when the MPM estimate was used for 64 kinds of halftone images obtained by conversion from the“Lena”image using the organized dither method via an 8×8 Bayer threshold array.Simulation showed that the optimal performance was achieved in the wide range of the parameterTmatJ=1.This result is evident in Fig.4(f).Then，perfect inverse halftoning was achieved when 256 kinds of halftone images were used，irrespective of the settings forJandTm，as shown in Fig.4(g).Next，when prior information was not used for the MPM estimate，as shown in Fig.4(h)，a false contour appeared in the image reconstructed using 16 kinds of halftone images.However，this contour was removed by appropriately introducing the model of the true prior，as shown in Fig.4(i).

Next，the performance of the MPM estimate was compared with other methods，such as the conventional Gaussian filter using the 3 ×3 kernel，the MAP estimation for a set of 16(64)halftone images of the 256－grayscale standard image“Lena”in Fig.2(a).As shown in Figs.10(a)，(b)and Figs.2(f)，(i)，it is found that the MPM estimate reconstructs original image more accurately than the conventional Gaussian filter via the 3 ×3 kernel，although the performance of the MPM estimate is almost the same as that of the MAP estimation.Also，it is found from the patterns of the reconstructed images in Figs.2(f)，(i)and Figs.10(a)，(c)，that the fatal contour will not appear in the reconstructed image obtained by the MPM estimate via the 16 halftone images if appropriate model of the true prior is used;however，that contour appeared in the patterns of the reconstructed images obtained by the Gaussian filter.

Fig.10 Reconstructed images obtained by the MAP estimation and the conventional filter using the 3×3 Gaussian kernelfor the256-grayscale standard image“Lena”with 256×256 pixels

3.4 Bethe approximation

Here a statistical mechanical iterative method is used with Bethe approximation to construct a practical and useful method.Bethe approximation has been used to approximate thermodynamics of many－body physical systems by solving the self－consistent equations on a set of effective fields.Here，a set of local magnetizations{mx，y}(0 ＜mx，y＜Q－1，x，y=1，2，…，L)is used on the square lattice to estimate macroscopic properties of the present method.Then，the set of the local magnetization{mx，y}is determined as a solution to the self－consistent equations:

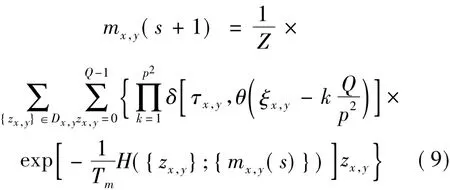
on{mx，y(s)}(0 ＜mx，y(s) ＜Q－ 1，x，y=1，2，…，L，s=0，1，2，…)，wheresdenotes the number of steps.Here， the effective HamiltonianH({zx，y};{mx，y(s)})in Eq.(9)is set as

Here，as shown in Fig.11，Dx，yis a set of lattice points{(x，y)，(x+1，y)，(x，y+1)，(x－1，y)，(x，y－ 1)}and{mx，y(s)}is a set of real numbers from 0 toQ－1 arranged on the lattice points aroundDx，y.The reconstructed image is obtained using the solution to the self－consistent equations in Eqs.(9)～(11):

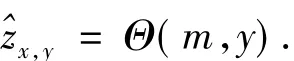
Fig.11 A set of pixels{zx，y}in Dx，y(Dx，y={(x，y)，(x+1，y)，(x，y+1)，(x－1，y)，(x，y－1)})and a set of effective fields{mx，y} around Dx，y.

To investigate the performance of the presented statistical mechanical iterative method，numerical simulation was conducted for the 256－grayscale “Lena”image with 256×256 pixels.The performance of Bethe approximation to carry out the Bayesian inference was estimated to obtain the MPM estimate.The results show that Bethe approximation obtains the reconstructed images in Figs.12(a)and(b)with 11～15 steps respectively by choosing initial halftone images，such as Fig.4(d).As shown in the case of the Monte Carlo simulation，it is found that false contour appears in the reconstructed image in Fig.12(a)and that such contour can be removed，as shown in Fig.12(b)，by the present method，using an appropriate model of the true prior.Here，the optimal value ofJ/Tmwas determined by trial and error without using a technique for parameter estimation，such as the EM algorithm［14－15］.

Fig.12 Reconstructed images obtained from the Bethe approximation using 16 kinds of the halftone images

From above results，it can be seen that the performance of the Bethe approximation is similar to that of MPM estimation which uses Monte Carlo simulation for realistic images，such as the 256－grayscale standard image“Lena”with 256×256 pixels.

4 Conclusion

As seen above，after outlining the statistical mechanics which is used to describe the thermodynamics of the spin model，an analogy between statistical mechanics and the MPM estimate was given based on Bayesian inference.Considering this analogy，the general formulation was then constructed for inverse halftoning using multiple halftone images.From the theoretical point of view，to determine the performance of the present method，Monte Carlo simulation was carried out to obtain a set of the snapshots of the Q－Ising model.It was found that the performance was optimal under the Bayes－optimal condition within statistical uncertainty，and that the optimal performance was superior to that of the MAP estimation.Then，using analytical estimation through building a mean－field infiniterange model，the properties obtained by the Monte Carlo simulation were qualitatively confirmed.Furthermore，it was found that the present method is effective even for realistic images if more than 64 kinds of halftone images are used.It was also found that the fatal contour will appear in the pattern conducted of the reconstructed image if the MPM estimate is conducted using fewer than 16 kinds of halftone images without using the model of the true prior，and that this contour can be removed by using the MPM estimate based on an appropriate model of the true prior.Finally，from the practical point of view，the performance of the statistical mechanical iterative method was evaluated using the Bethe approximation.Numerical simulation using the standard image“Lena”demonstrated that the Bethe approximation reconstructs the original image within 11～15 steps and that by using Monte Carlo simulation，Bethe approximation performs as good as the MPM estimate for this problem.From these results，it can be concluded that the statistical mechanical iterative method performs more effectively than the conventional MAP estimation.

Future work includes improving the performance of the statistical mechanical iterative method by using more accurate information on the model prior of grayscale images and on the MTF－function of the human vision system.Also，as the parameter selection is important in these problems based on the Bayesian inferences，the authors will construct a technique of inverse halftoning based on the parameter estimation using the EM algorithm.

［1］BESAG J.On the statistical analysis of dirty pictures［J］.Journal of the Royal Statistical Society—Series B:Statistical Methodological，1986，48(3):259－302.

［2］GONZALES R C，WOODS R C.Digital image processing［M］.Reading，USA:Addison Wiley，1986.

［3］WINKLER G.Image analysis，random fields and dynamic Monte Carlo methods:a mathematical introduction［M］.Berlin，Germany:Springer－Verlag，1995.

［4］NISHIMORI H.Statistical physics of spin glasses and information processing:an introduction［M］.Oxford，UK:Oxford Press，2001.

［5］TANAKA K.Statistical－mechanical approach to image processing［J］.Journal of Physics A:Mathematical and General，2002，35(37):R31－R150.

［6］ULICHNEY R.Digital halftoning［M］.Cambridge，USA:The MIT Press，1987.

［7］BAYER B E.An optimum method for two－level rendition of continuous tone pictures［C］//IEEE International Conference on Communications.New York，USA:IEEE Press，1973:11－15.

［8］MICELI C M，PARKER K J.Inverse halftoning［J］.Journal of Electronic Imaging，1992，1(2):143－151.

［9］WONG P W.Inverse halftoning and kernel estimation for error diffusion［J］.IEEE Transactions on Image Processing，1995，4(4):486－498.

［10］STEVENSON R L.Inverse halftoning via MAP estimation［J］.IEEE Transactions on Image Processing，1997，6(4):574－583.

［11］SAIKA Y，INOUE J，TANAKA H，et al.Bayes－optimal solution to inverse halftoning based on statistical mechanics of the Q－Ising model［J］.Central European Journal of Physics，2009，7(3):444－456.

［12］TIPPING M E，BISHOP C M.Bayesian image super－resolution［M］//BECKER S，THRUN S，OBERMAYER K.Advances in Neural Information Processing Systems.Cambridge，USA:The MIT Press，2003:1279－1286.

［13］KANEMURA A，MAEDA S，ISHII S.Superresolution with compound Markov random fields via the variational EM algorithm［J］.Neural Networks，2009，22(7):1025－1034.

［14］DEMPSTER A P，LAIRD N M，RUBIN D B.Maximumlikelihood from incomplete data via the EM algorithm［J］.Journal of the Royal Statistical Society—Series B:Statistical Methodological，1977，39(1):1－38.

［15］TANAKA K，INOUE J，TITTERINGTON D M.Probabilistic image processing by means of the Bethe approximation for the Q－Ising model［J］.Journal of Physics A:Mathematical and General，2003，36(43):11023－11035.

About the authors:

SAIKA Yohei，received a B.S.degree in physics from Tokyo Science University，Tokyo，Japan in 1989，an M.S.degree in physics from Tokyo Institute of Technology in 1991，and a Ph.D.degree in physics from Tokyo Institute of Technology in 1995.His research interests are statistical mechanics，application of physics to information，and optimization by means of quantum annealing.He worked with Wakayama National College of Technology，from 1995 to 2011，where he studied information science and technology related to image processing in the Department of Electrical and Computer Technology.Since 2011，he is working at Gunma National College of Technology，Maebashi，Japan.

AOKI Toshizumi，received a B.S.degree in physics from Nagoya University，Nagoya，Japan in 1976，an M.S.degree in physicsfrom NagoyaUniversity in 1978，and a D.Sc.in physics from Nagoya University in 1981.He has studied condensed matter physics，such as low－dimensional quantum systems.Since 1987，he is working at Gunma National College of Technology，Maebashi，Japan.

TP39

A

1643－4785(2012)01－0086－09

10.3969/j.issn.1673－4785.201111001

Date:2011－11－01.

SAIKA Yohei.E－mail:yoheisaika@gmail.com.