可满足问题中的模型计数

谷文祥，朱磊，黄平，殷明浩

(东北师范大学计算机科学与信息技术学院，吉林长春 130117)

可满足问题中的模型计数

谷文祥，朱磊，黄平，殷明浩

(东北师范大学计算机科学与信息技术学院，吉林长春 130117)

模型计数问题是指计算给定问题的解的个数，这是一类比决策更困难的问题，也是人工智能领域研究的一个热点问题.对模型计数问题的研究不仅可以提高算法的求解效率，更能促进对问题困难本质的了解.以可满足问题(命题可满足(SAT)和约束可满足问题(CSP))为例，从精确算法和近似求解两方面综述了模型计数问题的研究现状，重点介绍了相关概念以及各个算法之间的优缺点，并提出了有待解决的开放性问题，对模型计数问题的研究予以了总结和展望.

人工智能;约束可满足问题;命题可满足问题;模型计数

命题可满足问题(propositional satisfiability problem，SAT)的求解是近年来人工智能领域研究的热点问题，这类问题的计算复杂度是属于NP完全的［1］，也即意味着如果P≠NP成立，即无法在多项式时间内解决SAT问题.而模型计数问题是比这类决策问题更难解决的问题，它的计算复杂度是属于#P完全的.一些原本是多项式时间的决策问题的模型计数也是属于#P完全的，例如2SAT［2］.模型计数问题是指计算给定问题的解的个数，即使得公式值为真的不同的变量的赋值数.高效地解决模型计数问题对人工智能的很多领域都有着深远的影响，许多的概率推理如贝叶斯网络推理［3］等都可以转换为模型计数问题［2］.另一个应用是组合问题，计算解的个数能够更深入地了解问题的本质.对于组合这样的问题，即使找到一个解都是困难的，搜索整个解空间的模型计数问题的时间复杂度更是巨大的.这也就使得目前模型计数算法能解决问题的规模与决策性算法相比相差了好几个数量级.对于模型计数问题，目前确定性算法能够解决的问题的变量数约为几百个，近似算法能解决的问题的变量数约为1 000个.

约束可满足问题(constraint satisfaction problem，CSP)是SAT问题的一种泛化，当CSP问题中变量的取值为布尔值时，CSP问题就退化为普通的SAT问题.CSP问题的多值使得其在实际生活中有着更加广泛的应用，如图着色问题就是一种特殊的CSP问题，而规划问题也可以转换为动态CSP问题求解.CSP问题的模型计数(#CSP)方法大部分都是由求解SAT问题的模型计数(#SAT)方法扩展而来的，因此#CSP问题的求解也可分为2类:精确算法和近似求解.精确算法主要是以DPLL算法和局部搜索为基础，与决策问题只要找到一个可满足解不同，模型计数问题需要搜索整个解空间，因此算法的时间复杂度是巨大的.近似求解一般采用采样的方法来避免搜索整个解空间，利用局部解的数目来估计整个空间解的个数.这样使得算法的时间复杂度有了很大的改善，但是所得到解的数目却不再是精确的.本文将从以上2个方面分别介绍#SAT和#CSP问题求解算法的发展、相关概念以及算法的优缺点，并对模型计数问题的求解方向进行展望.

1 相关概念

本文讨论的模型计数问题都是基于SAT问题和CSP问题的.在介绍具体的算法之前，首先介绍一些与模型计数有关的定义.

定义1(命题可满足问题，SAT)给定一个命题逻辑公式F，其变量集为V=var(F)，是否存在对其变量集V的一个真值赋值，使命题公式F成立(可满足)，如果成立则返回这些变量真值赋值.

定义2(命题可满足问题的模型计数，#SAT)给定一个命题逻辑公式F，其变量集为V=var(F)，计算使得公式值为真的变量集V的赋值的个数，并返回这个值.

定义3(约束可满足问题，CSP)CSP问题可以描述为一个三元组P(X，D，C)，其中X是有限变量集合{X1，X2，…，Xn}，D为与X中变量对应的域值集合{D1，D2，…，Dn}，C是有限约束的集合，用于限制变量的取值.一个CSP问题就是找到一个满足约束C的变量集X的取值.

定义4(约束可满足问题的模型计数，#CSP)给定一个CSP问题P，计算所有使得P中约束满足的变量集的取值数目，并返回这个值.

由上面的定义可知，决策性问题可以看作模型计数问题的一种特殊情况.决策性问题只需找到一个可满足的解，而模型计数问题则要求找到问题的所有解.

在实际问题求解的过程中，一般将问题转换为图的结构.

定义5(约束图，GF) 给定一个命题逻辑公式F，F的约束图GF的定义如下:

1)GF中的顶点为F中的变量;

2)若F中的2个变量出现在同一个子句中，则在这2个变量所对应的顶点连上边.

约束图中的顶点表示原问题中的变量，而边表示变量之间的约束，问题的约束越多，则图的结构越紧密.

2 SAT中的模型计数

SAT问题是CSP问题的特殊实例，即SAT问题是域大小为2的CSP问题，相较于一般的CSP问题，SAT问题的模型计数比较简单，下面首先介绍有关SAT问题的模型计数方法.

2.1 精确算法

目前求解模型计数的方法有2种，即精确算法和近似求解.本文先介绍#SAT中主要的精确算法，然后给出典型的近似求解方法.

2.1.1 CDP算法

Valiant在1979年证明了模型计数问题是属于#P完全的［2］，即这是一类比NP问题更困难的问题.Dubois在1991年给出了一种求解SAT问题模型个数的方法，并且证明了时间复杂度为O()，其中n为变量数，m为子句数，ak是多项式ykyk－1－ … －1 的正根，k为子句的长度［4］.Zhang在1996年也给出了基于类似思想的算法，时间复杂度也近似相等［5］.虽然他们的算法都能够得到问题的解的数目，但是当问题规模增大时，算法的时间复杂度几乎是呈指数级增长，当k趋于无穷的时候，ak=2.Birnbaum和Lozinskii在1999年提出了基于SAT求解器DPP的CDP［6］，该方法不论是算法的复杂度还是时间复杂度上较前面的2个方法都有很大的改善.CDP(F，n)算法的基本框架如图1.

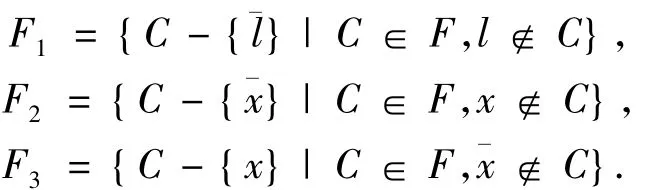
式中:l为单元文字，x为分支变量.

算法的输入参数为公式F和变量数n.首先判断公式是否为空，如果是，则表示公式已经被满足，所以返回解的个数为2n;反之公式若包含了空子句，则肯定不满足，返回0;若公式中有单元子句，则先对单元子句进行处理以简化公式，否则随机选择一个变量进行分支，分支后公式求得模型的总个数为原公式的模型数.

SAT求解器DPP找到一个可满足解就结束搜索，而CDP则需要搜索整个解空间，直到找到所有可满足的解，算法才结束.算法的时间复杂度为O(mdn)，其中，m为子句数，n为变量数，

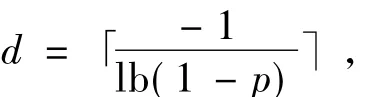
p为一个文字出现在一个子句中的概率.由于纯文字规则在模型计数中不能使用，因此分支变量的选择直接影响了算法的时间复杂度.作者提出了2种选择分支变量的方法，一是使得m2+m3的值尽可能小，m2、m3分别为F2、F3中的子句数，另外一种是使max(m2，m3)尽量小.通过实验得出，分支变量的选择使用第1种方法得到的效果明显比第2种方法好，但当这样的变量有多个时，可以用第2种方法确定下一个分支变量的摆选择.

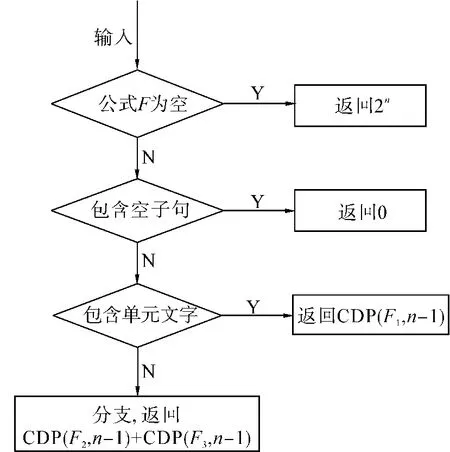
图1 CDP算法框架Fig.1 Framework of CDP

2.1.2 Relsat算法

在CDP算法中，如果当前的赋值使得公式的值为真，那么剩下变量的赋值则不会影响公式的真值，若当前已赋值的变量数为t，则模型的个数为2n－t.虽然这样可以加快算法的速度，但是算法的主要时间还是花费在分支计算上，如果能同时计算多个分支的模型个数，则算法的速度便可以得到很大的提高.由于CNF公式可以用约束图来表示，而各个独立的约束图可以看成是相互独立的组件，多个组件可以同步计算其模型的个数，因此可以将组件的思想应用于模型计数中，即算法 Relsat［7］.

2.1.3 Cachet算法

在Relsat算法中，主要是通过分别计算各个组件的模型数来得到公式的模型个数，如果在计算的过程中，出现了前面已经计算过的组件，利用Relsat求解算法则需重新计算一次，如果能在第1次计算时记录这个结果，在后续的搜索过程中得到同样的组件时，便可以直接使用缓存里面存储的结果.这和SAT求解器中的子句学习类似，利用空间换时间的方法.在Cachet算法中，同时使用了这2种方法:组件缓存和子句学习［8］.

Cachet算法主要是基于SAT求解器zchaff，直接应用组件缓存和子句学习使得算法求解出来的模型可能是实际问题模型的一个下界.为了避免这种情况，作者提出了用Routine remove siblings的方法来避免两者之间不必要的交叉.

Thurley在Cachet算法上利用不同的存储方式提高了算法的空间利用率.如算法存储的组件的子句至少有2个没有被赋值的变量，不显示存储原公式中的二元子句，并且存储的是组件中变量的索引以及属于组件的原始子句的索引.另外，在搜索时还加入了前向的搜索机制［9］.Davies和 Bacchus在搜索中的每个节点加入了更多的推理，如超二元归结和等式约简，也使得算法的效率有了很大的提高［10］.笔者还提出了利用归结的逆(扩展规则)来求解问题的模型数［11］.

2.1.4 cnf2ddnnf算法

前面提到的算法都是用不同的方法来直接求解给定的问题，而Darwiche在2004年改进了以前的知识编译算法，在SAT求解器zchaff的基础上提出了cnf2ddnnf算法［12］.算法的主要思想是将 CNF公式转换为确定的、可分解的否定范式的形式(ddnnf).在转换之前，首先要为原CNF公式F构造1棵分解树，这是一棵每个节点只有2个后代的二元树，叶子节点是F中的子句，每个节点都保存了一个称为separator变量集，里面存储的是左子树和右子树相同的变量.算法的主要思想是为separator变量集中的变量赋值，使得左右子树变量的交集为空，然后递归地构造分解树并将其转换为ddnnf的形式.

2.2 近似求解

模型计数的时间复杂度是属于#P完全的，这是比NP完全问题(如SAT问题的可满足性)更困难的一类问题.目前确定性算法能求解的问题的变量数约为几百个，对于更大规模的问题，这样的求解器是无能为力的.另一方面，在某些领域，并不一定要求得到问题精确的模型数，而只需要一个大概的估计.近似求解便能很好地满足这样的问题，近似求解算法不仅在时间复杂度上比确定性算法要低很多，而且能解决更大规模的问题.

2.2.1 ApproxCount算法

近似求解算法主要是基于采样的思想，在ApproxCount算法［13］中，用 SampleSAT［14］来进行采样.由于在采样的过程中使用随机行走算法，出现频率最高的解与出现频率最低的解相差了几个数量级;因此在SampleSAT算法中加入了MCMC(Markov chain Monte Carlo)来平衡随机行走，使得采样尽量均匀.

首先从公式F的解空间中进行K次采样(一个采样是公式的一个可满足的解)，K的值由算法的精确度决定.由于采样是均匀的，所以有

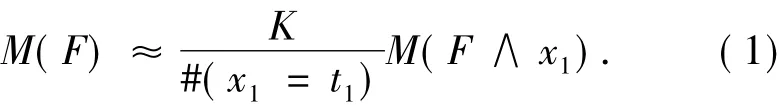
式中:#(x1=t1)是在K次采样中，x1取t1值的赋值数，设t1=true，M(F)为公式F的模型数.定义变量x1的乘数因子:

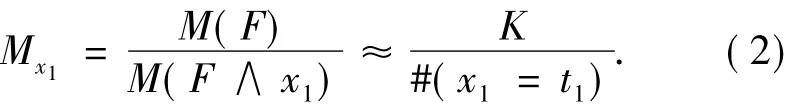
由式(1)和(2)，通过递归计算，可得公式F的模型数为

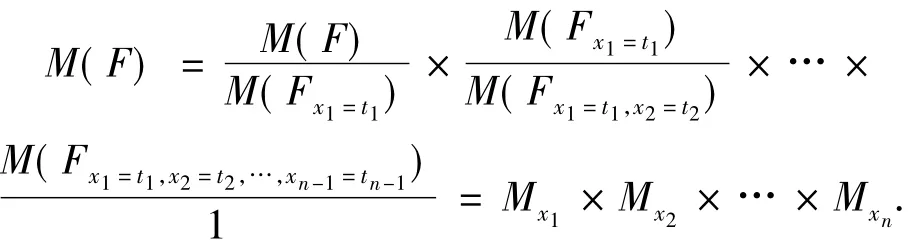
式中:Fx1=t1为F∧x1单元归结后的子公式，其他类似.

根据相变的原理，当C/V(子句数/变量数)小于某个值时，模型数很多，因此理论上搜索的时间也多，但是ApproxCount算法的搜索时间与C/V基本无关.

近似求解时会出现由于小误差的积累而导致大的误差，但是这种情况在ApproxCount算法中没有出现，因为有50%的时间步过高估计了乘数因子，而另外的50%过低估计了乘数因子，从而使得整个过程的求解偏差并不大.该算法是递增式进行的，每次设置一个变量的值，并且在每一步计算乘数因子.ApproxCount时间复杂度是关于问题规模的多项式时间的.

2.2.2 SampleCount算法

ApproxCount算法虽然能快速地估计问题的模型数，但是算法要求采样是均匀的，而进行均匀采样的复杂度是NP的，且算法对得到的结果没有保证.Gomes等在IJCAI07会议上提出的SampleCount算法避免了这样的问题［15］.

SampleCount算法主要是先为一些变量设定初值，直到化解后的子公式能够使用exact count算法进行求解，该算法与采样的质量(即是否为均匀采样)没有任何关系.主要是用 SampleSAT［14］作为启发式来指导设定初值的变量的选择，一般选择平衡变量，如果没有，则使用等价变量化解公式.该算法得到的公式的模型数为M(F)=2s－αM(G)，s为设定初值的变量数，α是松弛因子，M(G)为 exact count计算出的子公式确定的模型数.SampleCount算法不仅能保证得到的下界的正确率，而且即使采样是不均匀的也不会影响结果.算法精确度为1－2αt，t为迭代次数，α 是松弛因子，且 α ＞0.

2.2.3 MBound算法

MBound的主要思想是在原始的公式中加入XOR子句，对加入后的公式直接用SAT求解器进行求解［16］.由于在最好的情况下，加入XOR子句可以消减一半的解空间，即当加入s个XOR子句后，公式仍是可满足的，因此原公式至少有2s个模型.因为XOR约束可以有效地提供一个将解基本平分的hash函数，所以算法的求解与解在解空间中的分布没有关系.算法迭代t次，每次迭代中都加入s个XOR子句.若每次迭代的结果公式都是可满足的，则算法的下界为2s－α，其中α是松弛因子，且α＞0.上界2s+α也是类似得到的.如果在算法中将SAT求解器改为模型计数的求解器，算法的求解精度能进一步提高.

3 CSP中的模型计数

约束可满足问题是SAT问题的一种泛化，当CSP问题中变量的取值为布尔值时，CSP问题就变为了普通的SAT问题.CSP问题的多值使得其在实际生活中有着更加广泛的应用，如图着色问题和规划问题.目前求解CSP的模型计数问题的算法只能求解变量数在100以内的问题，且要花费大量时间.由此，设计一个好的求解CSP模型的算法就成为了一个急需解决的问题.

3.1 精确求解

目前关于#CSP精确求解的研究成果并不多，以下是主要的求解方法.

3.1.1 CSP2SAT算法

Angelsmark等在2002年给出了一种求解#CSP的方法，这种方法的主要思想是将原问题转换为相对简单的问题(2SAT)，通过求解转换后的问题的模型数来得到原问题的模型数［17］.

给定变量数为n，值域为d的二元CSP实例P.将P转换为多个2SAT实例I0，I1，…，Im，使得P的模型数与转换后的I0，I1，…，Im模型总数相同，其中m的大小与n、d的值均有关，每个实例Ik(k=0，1，…，m)中的变量对应P中变量的值，即Ik中的变量xe表示P中变量x取值为e.对于给定的变量x∈var(P)，e∈Dom(x)，则xe∈var(Ik)取值为真当且仅当变量x的赋值为e.实例Ik主要由两部分组成:1)与原问题中的约束对应的子句，即若P中有约束x≠y，则对所有的e，有﹁(xe∨ye).2)剩下的子句将由原问题中变量的域分对构成.如x∈var(P)，e1，e2∈Dom(x)，则加入子句(∨xe2)和(﹁xe1∨)，对于其他e∈Dom(x)且e≠e1，e≠e2，则添加﹁xe，由此来保证x只能取e1或者e2中的一个.若d为偶数，则有(d/2)n个实例，并且覆盖了原问题P;若d为奇数，作者给出了一种比较复杂的域的分法.整个算法的时间复杂度为:当d为奇数时，分2种情况考虑，当d=4k+1，时间复杂度为O(O(#2SAT)×((d2+d+2)/4)n/2);当d=4k+3，时间复杂度为O(O(#2SAT)((d2+d)/4)n/2)，其中O(#2SAT)是目前#2SAT问题最好的求解器所用的时间复杂度.3.1.2 CSP2wSAT算法

算法的主要思想是将CSP问题转换为weighted－2SAT问题，但要根据不同的d值，采用不同的方式.当d≤5时，问题直接转换，然后利用求解#weighted－2SAT模型个数的方法来求解原问题的模型个数;当d＞5时，将d分为小于5且不相交的集合，不同的集合代表不同的问题实例，然后分别将这些问题实例转换为weighted－2SAT问题，以这些实例的复杂度基底的和作为原问题复杂度的基底，由此得到了原问题的时间复杂度［18］.

该算法的时间复杂度为:

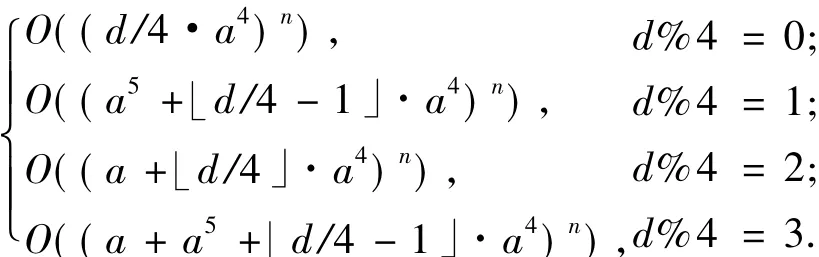
式中:a是#weighted－2SAT算法时间复杂度的上界基数，即O(#weighted－2SAT)=O(an).

3.1.3 BTD算法

Favier 等 利用 BTD(backtracking with tree－decomposition)的搜索方法来求解CSP问题的模型数.树分解的本质是对ci∩cj(cj是ci的儿子)的赋值能够把初始问题分成2个能独立求解的问题.树搜索中假定簇ci中变量的赋值总是先于ci儿子中变量的赋值，这样的变量排序可以利用树分解的性质.对于树中的簇ci，逐一对变量赋值，若出现冲突，则进行回退，直到ci中所有的变量都已经赋值.然后通过BTD算法计算ci的第1个儿子cj引导的子问题在赋值ci∩cj下的模型数，将ci在当前赋值下的模型的乘积返回，ci中所有赋值的模型数的和作为ci的模型数.最后得到c1的模型数即为要求解的问题的模型数［19］.该算法的时间复杂度是O(mndw+1)，其中，w为树宽.

3.2 近似求解

3.2.1 CSP+XOR算法

2006年，Gomes等将XOR应用于求解SAT问题的模型计数中，使得算法不仅能给出问题模型的上下界，还能对给定的结果进行评估［16］.2007年，他们扩展了这一思想，将XOR应用到求解CSP问题模型数［20］.

作者提出了2种实现方法.一是将CSP问题转换成SAT问题，然后直接加入二值的XOR，求解的过程和MBound算法相同.算法得到的模型个数的上下界和值的准确度也和MBound算法相同.另外一种是不需要转换，直接加入更一般的XOR约束到CSP问题中，算法得到的模型数的下界为ds－α，准确度为1－dαt，其中，s是问题中加入的XOR约束的数目，t是算法迭代的次数，α就是一个松弛因子.

3.2.2 ApproxBTD算法

前面介绍的BTD算法只能解决树宽比较小的问题，当问题的树宽比较大，且为稀疏图时，BTD算法会因为超时而不能给出问题的模型数.而Approx－BTD算法能够快速地给出更大规模问题的模型数近似值.

该算法主要思想是将图拆分成没有公共边的子图，且每个子图都是chordal的.对于每一个这样的子图，调用BTD求解，然后利用这些子图的模型数来估计原问题的模型个数［19］.

3.2.3 AE－count算法

许可等证明了用RB模型生成的随机CSP问题存在确定的相变点［21］，因此笔者也提出了一种近似求解 RB模型生成随机 CSP实例的算法——AE－count［22］.该算法主要利用了一阶矩和二阶矩在证明相变点位置时的特殊作用，证明了算法AE－count的时间复杂度是线性的，并且随着问题规模的增大，算法的精确度越高.定理1是该算法的主要的思想.

定理1［22］给定用RB模型生成的CSP实例I、k、α 和r满足不等式ke－α/k≥1(k≥1/(1 －p))和α ＞1/k，则当n→∞且满足p＜1－e－α/r(或r＜ －α/ln(1－p))时，

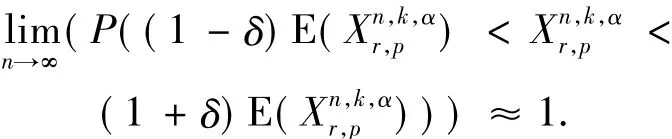
4 未解决的问题

模型计数问题是目前人工智能领域的研究热点之一，但还存在如下一些开放性的问题.

1)在SAT问题中，模型计数的确定性算法能解决的问题的变量数约为几百个，这与决策问题能解决的问题规模相差了好几个数量级.能否设计出计算大规模问题的确定性算法便成为一个亟需解决的难题.

2)相较于SAT问题，CSP问题结构更加复杂，所以求解时更加得困难.针对CSP问题本身的结构设计算法，以提高算法的求解效率，则是另一个需要进一步研究的问题.

5 结束语

本文给出了SAT和CSP问题目前主要的模型计数方法，并对算法的优缺点进行了评价.模型计数的精确算法只能解决小规模的问题，并且算法的时间复杂度随着问题规模增大呈指数级增长.将更多的规则应用到算法中，以减小解空间，从而快速地求出解数是该类算法的一个发展方向.近似求解能解决较大规模的问题，但是算法的复杂度随着算法的精度的提高和规模的增大而增大，AE－count算法不仅简单，而且当变量的值趋于无穷时，算法的精度为100%，可以作为精确算法.将AE－count应用于一般的#SAT和#CSP是下一步的工作重点，最后希望本文的工作能对相关人员的研究提供帮助.

［1］COOK S A.The complexity of theorem－proving procedures［C］//Proceedings of the Third Annual ACM Symposium on Theory of Computing.New York，USA:ACM，1971:151－158.

［2］VALIANT L G.The complexity of computing the permanent［J］.Theoretical Computer Science，1979，8(2):189－201.

［3］DARWICHE A.The quest for efficient probabilistic inference［R］.Edinburgh，UK:IJCAI，2005.

［4］DUBOIS O.Counting the number of solutions for instances of satisfiability［J］.Theoretical Computer Science，1991，81(1):49－64.

［5］ZHANG Wenhui.Number of models and satisfiability of sets of clauses［J］.Theoretical Computer Science，1996，155(1):277－288.

［6］BIRNBAUM E，LOZINSKII E L.The good old Davis－Putnam procedure helps counting models［J］.Journal of Artificial Intelligence Research，1999，10(1):457－477.

［7］BAYARDO R J Jr，PEHOUSHEK J D.Counting models using connected components［C］//Proceedings of the Seventeenth National Conference on Artificial Intelligence and Twelfth Conference on Innovative Applications of Artificial Intelligence.Austin，USA，2000:157－162.

［8］SANG T，BACCHUS F，BEAME P，et al.Combining component caching and clause learning for effective model counting［C/OL］. ［2011－07－20］.http://cs.rochester.edu/ ～ kautz/papers/modelcount－sat04.pdf.

［9］THURLEY M.SharpSAT:counting models with advanced component caching and implicit BCP［M］//BIERE A，GOMES C P.Theory and Applications of Satisfiability Testing.Seattle，USA:Springer，2006:424－429.

［10］DAVIES J，BACCHUS F.Using more reasoning to improve#SAT solving［C］//Proceedings of the 22nd National Conference on Artificial Intelligence.Vancouver，Canada，2007:185－190.

［11］YIN Minghao，LIN Hai，SUN Jigui.Counting models using extension rules［C］//Proceedings of the 22nd National Conference on Artificial Intelligence.Vancouver，Canada，2007:1916－1917.

［12］DARWICHE A.New advances in compiling CNF into decomposable negation normal form［C］//Proceedings of the 16th Eureopean Conference on Artificial Intelligence.Valencia，Spain，2004:328－332.

［13］WEI W，SELMAN B.A new approach to model counting［M］//FAHIEM B，WALSH T.Theory and Applications of Satisfiability Testing.St.Andrews， UK: Springer，2005:324－339.

［14］WEI W，ERENRICH J，SELMAN B.Towards efficient sampling:exploiting random walk strategies［C］//Proceedings of the 19th National Conference on Artificial Intelligence，Sixteenth Conference on Innovative Applications of Artificial Intelligence.San Jose，USA，2004:670－676.

［15］GOMES C P，HOFFMANN J，SABHARWAL A，et al.From sampling to model counting［C］//Proceedings of the 20th International Joint Conference on Artificial Intelligence.San Francisco，USA:Morgan Kaufmann Publishers Inc，2007:2293－2299.

［16］GOMES C P，SABHARWAL A，SELMAN B.Model counting:a new strategy for obtaining good bounds［C］//Proceedings of the Twenty－First National Conference on Artificial Intelligence and the Eighteenth Innovative Applications of Artificial Intelligence Conference. Boston，USA，2006:54－61.

［17］ANGELSMARK O，JONSSON P，LINUSSON S，et al.Determining the number of solutions to binary CSP instances［C］//Proceedings of the 8th International Conference on Principles and Practice of Constraint Programming.Ithaca，USA，2002:327－340.

［18］ANGELSMARK O，JONSSON P.Improved algorithms for counting solutions in constraint satisfaction problems［C］//Proceedings of the 8th International Conference on Principles and Practice of Constraint Programming.Kinsale，Ireland，2003:81－95.

［19］FAVIER A，GIVRY S D，JEGOU P.Exploiting problem structure for solution counting［C］//Proceedings of the 15th International Conference on Principles and Practice of Constraint Programming.Lisbon，Portugal，2009:335－343.

［20］GOMES C P，Van HOEVE W J，SABHARWAL A，et al.Counting CSP solutions using generalized XOR constraints［C］//Proceedings of the 22nd National Conference on Artificial Intelligence.Vancouver，Canada，2007:204－209.

［21］XU Ke，LI Wei.Exact phase transitions in random constraint satisfaction problems［J］.Journal of Artificial Intelligence Research，2000，12:93－103.

［22］HUANG Ping，YIN Minghao，XU Ke.Exact phase transitions and approximate algorithm of#CSP［C/OL］.［2011－07－20］.http://www.aaai.org/ocs/index.php/AAAI/AAAI11/paper/view/3508/4142.

谷文祥，男，1947年生，教授，博士生导师，主要研究方向为智能规划与规划识别、形式语言与自动机、模糊数学及其应用.参与或承担多项国家自然科学基金项目、教育部重点项目、省科委项目，发表学术论文100余篇.

朱磊，男，1987年生，硕士研究生，主要研究方向为智能规划、智能信息处理.

黄平，女，1986年生，硕士研究生，主要研究方向为智能规划与规划识别.

The model counting of a satisfiability problem

GU Wenxiang，ZHU Lei，HUANG Ping，YIN Minghao
(School of Computer Science and Information Technology，Northeast Normal University，Changchun 130117，China)

A model counting problem refers to computing the number of solutions for a given problem which is harder than the decision－making problem.Model counting problems are also a hot topic in the field of artificial intelligence.Research on model counting problems can not only improve the efficiency of an algorithm，but also enhance the understanding of the nature of hard problems.Taking a satisfiability problem in propositional logic，known as an SAT，and a constraint satisfaction problem(CSP)as an example，a model counting problem was reviewed from two aspects:an exact algorithm and approximate algorithm.For each aspect，the development and related concepts along with the advantages and disadvantages were emphasized.Moreover，this paper proposed some unsolved questions of the model counting and gave a summary and outlook of the research on model counting.

artificial intelligence;constraint satisfaction problem;propositional satisfiability problem;model counting

TP18

A

1673－4785(2012)01－0033－07

10.3969/j.issn.1673－4785.201107008

http://www.cnki.net/kcms/detail/23.1538.TP.20120217.1520.001.html

2011－07－25. 网络出版时间:2012－02－17.

国家自然科学基金资助项目(61070084，60573067，60803102).

黄平.E－mail:huangp218@nenu.edu.cn.