扭转梁式后悬架结构参数对侧倾振动影响

江浩斌，李 超，徐 兴，黄如波，赵水平

(1.江苏大学 汽车与交通工程学院，江苏 镇江212013;2.泛亚汽车技术中心，上海201201)

扭转梁式后悬架具有许多优点，如结构简单，制造成本低，占用空间少，后排空间和行李箱容积大，在运动中外倾角变化小，减振器与弹簧易匹配，且不会发生应力弯曲等，被广泛应用于紧凑型轿车。同时，也存在横梁及焊缝处应力高，橡胶衬套应力复杂等缺点。扭转梁式后悬架结构参数对车辆操纵稳定性和平顺性均有重要影响，国内外学者也进行了广泛深入研究。目前，主要采用有限元模型、刚柔耦合模型、等效动力法等手段研究了扭转梁结构参数对悬架运动学特性、轮胎非正常磨损、车轮定位参数、结构优化等内容［1-2］。扭转梁式后悬架系统示意如图1。

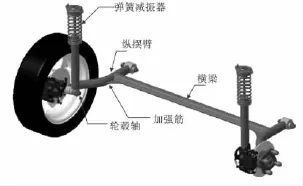
图1 扭转梁式后悬架系统示意Fig.1 The structure of the twist beam suspension

扭转梁式后悬架兼有非独立和独立悬架的特点。在车辆振动分析中，若将其完全视为非独立悬架则忽略了其独立的特点。笔者忽略车身刚度、橡胶衬套刚度及扭转梁悬架很小的阻尼系数等影响因素，进行合理假设和简化，并在有限元软件中测定了扭转梁悬架扭转刚度［3］。建立了包含扭转梁式悬架系统的整车8自由度平顺性模型和车辆瞬态侧倾模型，运用MATLAB/Simulink仿真分析了扭转梁式悬架系统对平顺性和车辆瞬态侧倾的影响。这在初期设计及产品更新换代阶段，尤其是许多参数尚未确定时，可以指导载荷-变形分析等结构参数设计，快速预估扭转梁悬架对汽车侧倾响应的影响。

1 扭转梁悬架运动学分析

假定扭转梁悬架剪切中心与质心重合，车辆振动时，选取左后轮振动系统的侧面图(图2)［4］。

图2 扭转梁悬架运动学分析Fig.2 Kinematics analysis of the twist beam suspension

在垂向运动时(图2)，扭转梁悬架质心在XOZ面内俯仰角度φt为:

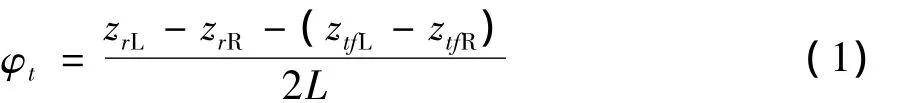
扭转梁悬架侧倾角度θt为:

横梁的扭转角度φb约为:

纵摆臂在车轮安装点处和车身安装点在垂直方向所受到的力分别为:

由此可知，车身安装点跨距越大，越有利于降低橡胶衬套等的受力，提高疲劳寿命。

左右轮不同激励方向和位移时，扭转梁悬架吸收力矩为:

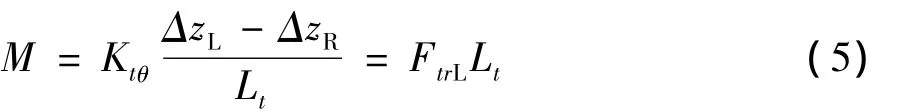
Ktθ为扭转梁悬架扭转刚度，其侧倾角刚度为:

由后悬架系统的运动学，以及文献［5］中所描述的疲劳裂纹方向可知，沿从前铰接点到剪切中心的连线旋转，沿该旋转轴线建立静力学力矩平衡方程:

由此可知，扭转梁悬架的剪切中心和铰接点位置等对受力关系具有重要影响。

2 仿真模型

2.1 整车8自由度平顺性模型

首先假设如下:路面的不平度系数不变，仅与所选的路面等级有关;忽略橡胶衬套、车身刚度、发动机扭振、车轮不平衡度等影响因素;匀速直线运动时，车身微幅振动。建立整车8自由度平顺性模型［6］，如图 3。

图3 整车8自由度平顺性模型Fig.3 The vehicle 8-DOF ride model

车身与悬架、扭转梁连接处以及座椅的垂直位移有如下关系:

车身与前后悬架及座椅连接处的作用力分别为:

车身质心处的垂向、侧倾、俯仰运动学微分方程为:

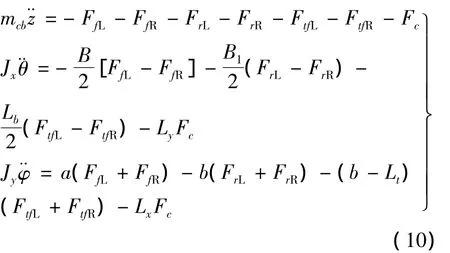
车轮及座椅的运动学微分方程为:

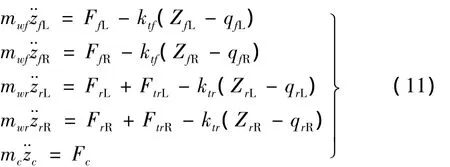
综上所述，取 z、zfL、zfR、zrL、zrR、zb、θ、φ 为状态变量，建立微分矩阵方程如式(12):

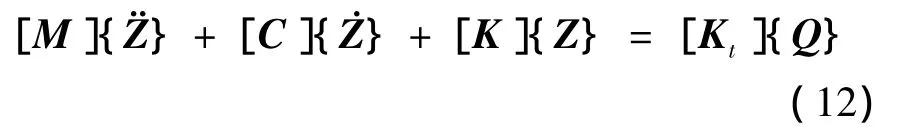
取微分方程各项状态变量的系数，质量矩阵M、阻尼矩阵C、刚度矩阵K和输入矩阵Q。受篇幅所限，省略了各矩阵具体参数。

2.2 瞬态侧倾模型

在侧倾平面内，忽略道路颠簸不平、横向风、轮胎弹性变形等影响因素，刚性车辆瞬态侧倾模型如图 4［7］。

图4 瞬态侧倾模型Fig.4 Transient roll model

车辆瞬态侧倾模型的运动学微分方程［3］为:

式中:Kf、Kr、Kt分别为前、后轴单侧垂向刚度和扭转梁悬架引起的侧倾角刚度;C为前后轴等效侧倾阻尼系数;ay为质心处侧向加速度。

3 仿真分析

根据上述动力学公式，建立Simulink仿真模型，对比分析不含扭转悬架的简化模型(即令Ktθ=0)和含扭转梁悬架整车模型，汽车主要结构参数为:mcb=780 kg，mc=75 kg，mwf=25.5 kg，mwf=60 kg，Jx=493 kg·m2，Jy=523 kg·m2，B=1.225 m，a=0.977 m，b=0.788 m，ksf=13 350 N/m，ksr=13 787 N/m，csf=1 156 N·m/s，Lt=0.355 m，csr=1 050 N·m/s，cc=700 N·m/s，m=1.17 m，kc=10 000 N/m，ktf=ktr=19 200 N/m，Lb=0.992 m，s=0.118 m。

3.1 B 级路面

路面输入采用积分白噪声模型，前后轮处路面输入相差一个时间滞后量，即为轴距与车速之比，以50 km/h车速行驶在B级路面时，激励信号如图5。

图5 B级路面时域信号Fig.5 The B-class road at a speed of 50km/h

座椅垂直加速度、座椅垂直加速度功率谱、车身垂直加速度功率谱仿真结果如图6～图8。

图6 座椅垂直加速度Fig.6 Seat vertical acceleration

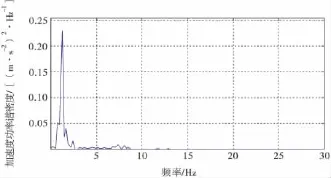
图7 座椅垂直加速度功率谱Fig.7 Seat vertical acceleration power spectrum

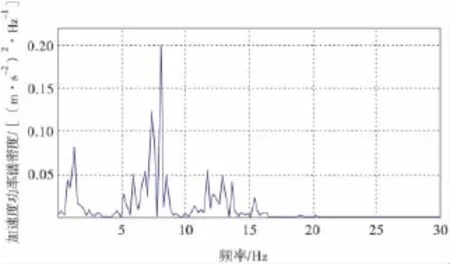
图8 车身垂直加速度功率谱Fig.8 Body vertical acceleration power spectrum

由图7可以看出，座椅振动集中在2～3 Hz频率范围内。从图8可以看出，车身的振动主要集中在2～3 Hz、5～10 Hz以及12～15 Hz频率的范围内。

3.2 正弦波扭曲路面

忽略车轮接地性等影响因素，微型车只需通过80 mm的左右两排互相交错分布的丙种正弦波扭曲路，扭转梁悬架对车身侧倾振动的影响，如图9～图11。

图9 正弦波扭曲路面Fig.9 Twist sinusoid road

图10 50 km/h B级路面车身侧倾角对比Fig.10 The roll angle on the B-class road at a speed of 50 km/h

图11 10 km/h正弦波扭曲路车身侧倾角对比Fig.11 The roll angle on the twist sine road at a speed of 10 km/h

仿真结果表明:在B级路面，因左右轮激励方向和大小基本相同，扭转梁悬架扭转角度很小，基本不发挥作用，在平顺性方面，与简化模型对比基本无差异;但在正弦波扭曲恶劣路面时，扭转梁悬架提高了侧倾角刚度而降低了车身侧倾角振幅，一定程度上提高了平顺性。此外，也表明在强化路面行驶时，笔者所建立地模型优于简化仿真模型。

3.3 车身侧倾振动分析

假设初始条件为0时，对式(14)进行拉氏变换，系统的传递函数为:

根据单自由度无阻尼振动系统相关理论［8］可知，车身侧倾固有圆频率为:

绘制出扭转梁悬架扭转刚度、纵摆臂长度与车身侧倾角固有频率之间的关系曲线，如图12。结果表明:纵摆臂越短，扭转梁悬架扭转刚度越大，则车身侧倾角固有频率越高，故应合理设计纵摆臂长度和扭转刚度，避开侧倾振动的敏感范围为0.6～1.0 Hz。

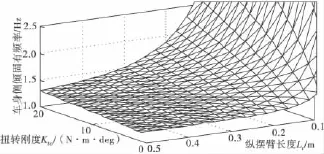
图12 车身侧倾角固有频率变化情况Fig.12 The change of the roll angle natural frequency

以加装扭转梁悬架扭转刚度Ktθ=13 N·m/deg为例，在侧向加速度脉冲激励下，对比有无扭转梁悬架时车辆侧倾角脉冲响应曲线，如图13。

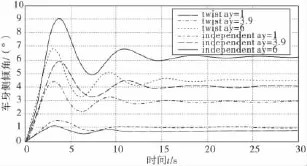
图13 车身侧倾角响应曲线Fig.13 The impulse response curve of roll angle

扭转梁悬架的扭转刚度、纵摆臂长度对车身侧倾角、车身侧倾固有频率、瞬态侧倾特性(如最大超调量、调整时间、峰值时间)等具有重要影响。纵摆臂越短，扭转梁悬架扭转刚度越大，车身侧倾角固有频率越高，舒适性降低，侧倾阻尼决定了侧倾角速度和超调量，将影响在某些工况下侧倾振动特性，故应合理设计扭转梁悬架系统结构及相关参数，确定合适的固有频率等参数，以满足动态性能要求。

4 试验验证

由于扭转梁式后悬架样车正在试制阶段，暂对类似样车进行试验，试验仪器主要有座椅三向加速度传感器、速度传感器、车速传感器、陀螺仪、电荷放大器、数据采集器等(图14)。参照 GB/T 4970—1996标准要求，以50 km/h车速行驶在B级路面时进行了平顺性随机输入行驶试验。参照 GB/T 6323.6进行了稳态回转试验。

图14 试验仪器Fig.14 Test instrument

4.1 平顺性随机输入行驶试验

经数据处理系统分析Z向加速度信号后，座椅的加速度功率谱密度曲线如图15。图15表明二者在峰值频率上吻合良好。因道路不平度激励差异、试验设备、数据分析设备误差等造成峰值大小存在一定差异，但是也验证了平顺性仿真模型是可信的。

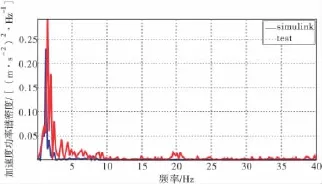
图15 座椅垂直加速度功率谱试验值与仿真值对比Fig.15 Test seats vertical acceleration power spectrum

4.2 稳态回转试验

在0.4 g侧向加速度时，样车车身侧倾角试验值约为4.17°，仿真结果为4.1°。由于仿真模型忽略了车身及部分结构的柔性，仿真值稍低于试验值。同时也表明，扭转梁悬架能降低车身侧倾角稳态值，车辆侧倾角与侧向加速度近似于线性关系，见图16。

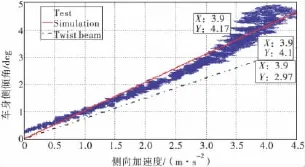
图16 侧倾角与侧向加速度关系曲线试验与仿真Fig.16 Roll angle vs lateral acceleration curves of test and simulation

5 结语

扭转梁悬架系统在积分白噪声仿真路面时，类似于横向稳定杆作用机制，因左右轮激励基本相同，扭转角度很小，它基本不发挥作用［9］。

笔者揭示了扭转梁悬架的扭转刚度、纵摆臂长度与车身侧倾角、车身侧倾固有频率、瞬态侧倾特性等之间的关系，纵摆臂越短，扭转梁悬架扭转刚度越大，车身侧倾角固有频率越高，故应合理设计扭转梁悬架结构参数。此外，在保证悬架侧倾角刚度的前提下，为采取降低弹簧刚度方法来提高平顺性提供了改进空间。扭转梁悬架剪切中心位置和旋转轴线对受力方向和大小均具有重要影响，将间接影响整车平顺性、操纵稳定性和零部件疲劳寿命等。

［1］黄海波.轿车轮胎非正常磨损机理及使用寿命预测研究［D］.上海:同济大学，2008:23-25.

［2］Mun K J，Kim T J，Kim Y S.Analysis of the roll properties of a tubular-type torsion beam suspension［J］.Journal of Automobile Engineering，2010，224(1):1-13.

［3］沈舒骋，沈浩，吴光强，等.复合式悬架车桥动力学参数分析［J］.上海汽车，2002(1):15-17.Shen Shucheng，Shen Hao，Wu Guangqiang，et al.The analysis on the kinematics of the twist beam suspension［J］.Shanghai Automobile，2002(1):15-17.

［4］［德］M.米奇克.汽车动力学［M］.4版.陈荫三，余强，译.北京:清华大学出版社，2009:379-407.

［5］陈立杰，谢里阳，李文辉，等.桑塔纳汽车后桥强度有限元分析及改进方案［J］.汽车工程，2004，26(4):488-491.Chen Lijie，Xie Liyang，Li Wenhui，et al.Finite element analysis and improvement scheme for rear axle of Santana car［J］.Automotive Engineering，2004，26(4):488-491.

［6］［英］Dave Crolla，喻凡.车辆动力学及其控制［M］.北京:人民交通出版社，2004:96-99.

［7］吴生玉.基于 ADAMS的车辆侧倾运动研究［D］.南京:南京航空航天大学，2007.

［8］于长官.现代控制理论［M］.3版.哈尔滨:哈尔滨工业大学出版社，2005:14-15.

［9］王蠡，项党，陈璟，等.扭力梁后桥总成参数对整车转向特性影响的分析.［J］.汽车工程，2011，33(1):61-64.Wang Li，Xiang Dang，Chen Jing，et al.An analysis on the effects of the parameters of twist beam rear axle on vehicle steering characteristics［J］.Automotive Engineering，2011，33(1):61-64.