适用于OFDM系统的符号定时盲同步技术
2012-08-16许炜阳
许炜阳
(重庆大学 通信工程学院,重庆400044)
作为一种高速无线传输技术,OFDM具有很强的抗多径衰落和脉冲干扰能力,已经成功应用在多种通信标准中,具有非常广阔的发展前景[1]。相比于单载波系统,同步算法对OFDM系统尤其重要。同步算法中的符号定时同步其目的是估计出DFT窗口的起始点,以便进行解调,避免产生载波间干扰(ICI)和符号间干扰(ISI)[2]。
符号定时同步算法可以分为数据辅助型和非数据辅助型(也叫盲算法)两大类。数据辅助型方法有较高的精度和较低的复杂度;但是由于需要周期性发送训练序列和导频,占用了有效带宽,因此不适用于某些频谱资源受限的场合[3-5]。与此同时,具有高频谱利用率的盲算法成为学术界的研究热点。盲同步算法是指不借用训练符号和导频,而利用OFDM符号本身的一些特性,这些特性包含了符号同步信息。循环前缀(Cyclic Prefix,CP)是OFDM系统本身就具有的重复信息,利用CP进行同步不需要额外的开销就能完成定时估计[6-8]。Van de Beek[6]较早地对利用CP实现符号同步进行了深入研究,并且提出了相应的基于最大似然准则的同步方法。然而在无线环境中,由于多径信道破坏了CP与原来数据的相关性,算法性能较差。A.Al-Dweik,等[9]提出了适用于恒定包络星座图OFDM系统的符号定时误差估计算法,假设无线信道保持不变,通过最小化相邻符号间相同子载波上的能量差进行同步。其缺陷在于只适用于恒定包络调制,应用范围有限。
笔者提出一种适用于OFDM系统的符号定时盲同步算法,其核心思想是如果不存在ICI和ISI,接收信号有最大非高斯性,用统计学上的峰度表征,通过最大化峰度就可以估计出定时误差。算法适用于任意星座图映射,具有普适性。
1 符号定时误差的影响
符号定时误差有正负两种情况(图1)。
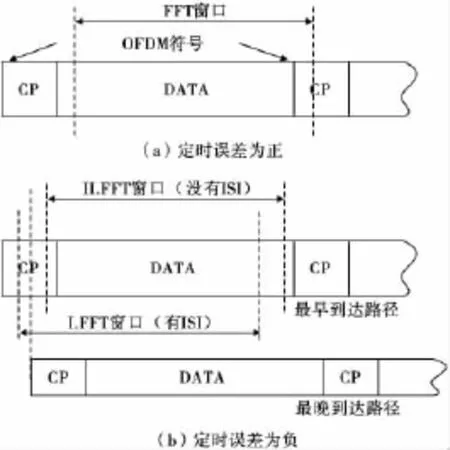
图1 符号定时误差示意Fig.1 Illustration of symbol timing errors
如果定时误差为正,DFT窗口同时包含当前符号和下一个符号的数据,不可避免产生干扰;如果定时误差为负值,可以分两种情况分析,如图1(b)。由于存在循环前缀,如果定时点落在τmax-Ng≤μ≤0区域内(μ是定时点,Ng是循环前缀长度,τmax是信道延迟,T是采样周期),那么DFT窗口内的数据都来自当前符号。利用DFT的性质可以推导出解调后的数据中会存在相位旋转因子,但不会引入符号干扰:

因此,学术界将τmax-Ng≤μ≤0称为安全区域(safe region)。另一方面信号传送由于受到多径效应的“拖尾”影响,循环前缀中存在一个符号干扰区域,如图1(b)。如果符号定时点落在这个区域,则会产生符号间干扰:
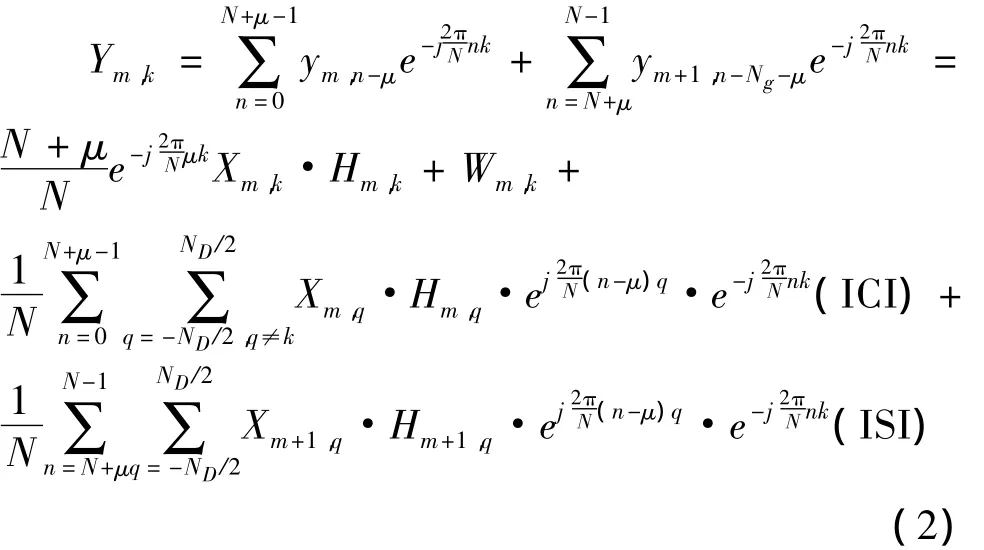
可以发现,Ym,k包括本来的有用数据部分、ISI、ICI和高斯噪声。受到符号定时误差的影响,原本子载波上信号的幅度会衰减,并且相位也会旋转;同时符号干扰与载波干扰等效于在解调信号中引入了额外的噪声,从而恶化系统性能。
2 符号定时误差估计算法
2.1 算法原理及复杂度分析
通过对符号定时误差对接收信号影响的分析,可以发现,如果DFT窗口的起始点落在安全区域内,解调信号为发送信号乘上信道频率响应;否则DFT窗口包含两个不同符号中的数据,会引入符号间干扰和载波间干扰。从式(2)可以发现,接收信号为N个发送信号的线性叠加,根据中心极限定律,独立同分布的随机变量的线性叠加,其分布相比于原来变量更加接近于高斯分布[10]。因此,当DFT窗口的起始位置位于安全区域时,接收信号的非高斯性大于存在符号定时误差情况下接收信号的非高斯性,这即是本文的核心思想。这里采用统计学上的峰度(kurtosis)来表征非高斯性的大小,因为计算信号的峰度相对简单。一个随机变量的峰度定义为:
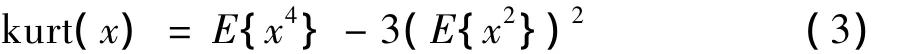
因此,本文价值函数可以表示为:
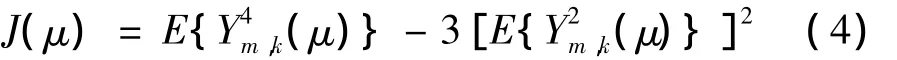
符号定时误差并不会改变接收信号的能量,因此式(4)中的第2项可以忽略。如果子载波数足够大,期望值可以近似为在所有子载波上求平均,价值函数进一步改写为:

式中:M为OFDM符号数。
定时误差可能值为μ∈{-(1/2)(N+Ng),…,(1/2)(N+Ng)},为了得到定时误差估计值,需要计算价值函数在所有可能值处的取值,其中的最小值即对应符号定时点。
表1给出了本文算法与文献[9]算法的复杂度对比,利用两个连续的OFDM符号求平均值。可以发现本文算法的复杂度约为文献[9]算法的1/3。为了更进一步说明问题,这里给出文献[9]算法的价值函数并且展开得到:

分析可以发现,本文算法的价值函数实际上只是式(6)的第1项,因此可以降低复杂度。

表1 本文算法与文献[9]算法的复杂度对比Table 1 Complexity comparison between proposed and reference[9]
2.2 优化性能
图2是算法价值函数的归一化实现样本,采用 AWGN信道,QPSK调制,N=64,Ng=16。由于是AWGN信道,因此,安全区域长度为16。正如图2中的平坦区域,证明了前面分析的正确性。
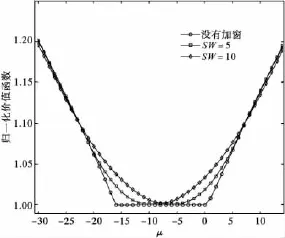
图2 不同滑动窗口长度下归一化价值函数Fig.2 Normalized cost function with different sliding windows
在安全区域边界处价值函数的取值和安全区域内的取值是比较相近的,存在噪声的情况下,其取值很可能小于安全区域内的取值,这种情况是算法估计出现错误的主要原因。为了提高算法的有效性,笔者采用滑动窗口(Sliding Window,SW)的方法。具体实现步骤为:首先计算每个可能定时点的价值函数;然后针对每一点的取值,用其左右两边SW长度的所有值之和代替当前值。图2也给出了采用滑动窗口后的归一化价值函数。可以发现随着滑动窗口长度的增加,曲线变得更加尖锐,价值函数的最小值离安全区域的边界越来越远,从而提高估计的精度。
3 算法仿真
为验证算法,笔者给出了计算机仿真结果。仿真采用的OFDM系统总共包含64个子载波,循环前缀长度为16;无线信道采用5径瑞利多径衰落模型,归一化延迟为[0,1,2,6,11],增益为[0.34,0.28,0.23,0.11,0.04]dB。所有结果都是经过 5 000 次蒙特卡洛仿真得到。
采用学术界通用的锁定概率Plock-in来衡量算法性能,锁定概率定义为同步算法将定时点设在安全区域内的概率[11]。图3给出了本文算法与Dweik算法[9]的锁定概率性能对比。利用20个OFDM符号求平均,滑动窗口长度为5,假设信道恒定不变,即多普勒频移fd=0。本文算法采用多种调制方式,Dweik方法采用QPSK调制。
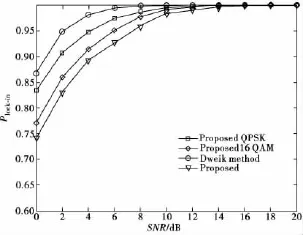
图3 fd=0 Hz时两种算法Plock-in性能对比Fig.3 Performance comparison with fd=0 Hz
从图3中可以发现,Dweik方法有最低的锁定概率。由于信道恒定不变,因此,Dweik方法可以有效利用最小化相邻符号相同子载波上的数据能量差,但是只适用于恒定包络调制。本文算法适用于任意星座图映射,但是性能不如Dweik算法,这是因为峰度是一个统计量,要准确地表征需要利用无穷多个OFDM符号,采用有限的符号数必然带来差错。同时注意到随着星座图点数增加,本文算法性能有所下降。
图4给出了当fd=200Hz的情况下,两种算法的性能对比。
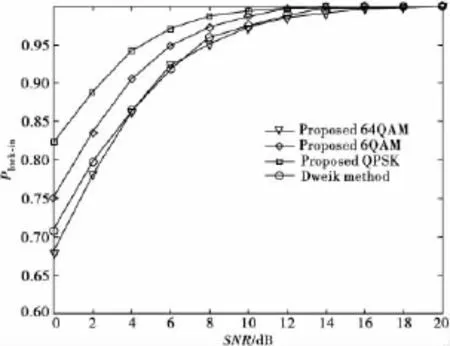
图4 fd=200 Hz时两种算法Plock-in性能对比Fig.4 Performance comparison with fd=200 Hz
首先发现由于信道存在时变性,相邻符号间的信道不完全相等,Dweik算法的前提假设不再成立,所以其性能明显下降。当SNR=0 dB时,锁定概率由图3的0.87降为图4的0.7左右。同时,本文算法的性能也有所下降,但是相比于Dweik算法来说,本文算法更加不易受信道时变性的干扰。比如,当SNR=0 dB时,算法采用QPSK调制,锁定概率由图3的0.84降为图4的0.82。这是由于本文算法是基于最大化接收信号的非高斯性,而不是假设信道保持不变。
4 结语
提出了一种适用于OFDM系统的符号定时盲同步算法。研究发现如果符号定时点位于安全区域内,接收信号有最大非高斯性,用统计学上的峰度表征;接收机通过最大化接收信号的峰度估计定时误差。算法不需要训练符号,频谱利用率较高。通过滑动窗口技术可以提高估计精度。仿真结果表明较之于现有方法,该估计算法具有普适性;同时可以更加有效地对抗信道的时变性。
[1]佟学俭,罗涛.OFDM移动通信技术原理与应用[M].北京:人民邮电出版社,2003.
[2]Morelli M,Kuo C C J,Pun M O.Synchronization techniques for orthogonal frequency division multiple access(OFDMA):a tutorial review[J].Proceedings of the IEEE,2007,95(7):1394-1427.
[3]Schmidl T M,Cox D C.Robust frequency and timing synchronization for OFDM[J].IEEE Transaction on Communications,1997,45(12):1613-1621.
[4]Minn H,Bhargava V K,Letaief K B.A robust timing and frequency synchronization for OFDM systems[J].IEEE Transactions on Wireless Communications,2003,2(4):822-839.
[5]Lv Tianjun,Li Hua,Chen Jie.Joint estimation of symbol timing and carrier frequency offset of OFDM signal over fast time-varying multipath channels[J].IEEE Transactions on Signal Processing,2005,53(12):4526-4535.
[6]Van de Beek J J,Sandell M,Börjesson P O.ML estimation of time and frequency offset in OFDM systems[J].IEEE Transactions on Signal Processing,1997,45(7):1800-1805.
[7]Hsieh M H,Wei C H.A low-complexity frame synchronization and frequency offset compensation scheme for OFDM systems over fading channels[J].IEEE Transactions on Vehicular Technology,1999,48(9):1596-1609.
[8]Lashkarian N,Kiaei S.Class of cyclic-based estimators for frequency-offset estimation of OFDM systems[J].IEEE Transactions on Communications,2000,48(12):2139-2149.
[9]Al-Dweik A,Younis S,Hazmi A,et al.Efficient OFDM symbol timing estimator using power difference measurement[J].IEEE Transactions on Vehicular Technology,2012,61(2):509-520.
[10]Yao Yingwei,Giannakis G B.Blind carrier frequency offset estimation in SISO,MIMO,and multiuser OFDM systems[J].IEEE Transactions on Communications,2005,53(1):173-183.
[11]Zhu Qingyu,Liu Zhiqiang.Minimum interference blind time-offset estimation for OFDM systems[J].IEEE Transactions on Wireless Communications,2006,5(8):2136-2142.
