基于LM算法的双流化床循环流率预测模型研究

陈鸿伟, 祁海波, 梁占伟, 杨 新

(华北电力大学能源动力与机械工程学院,保定 071003)

当今世界经济的高速发展以化石能源的过度消耗为代价,对化石燃料的过度依赖造成了世界范围的能源危机,大力发展可再生能源是解决能源危机实现可持续发展的必然要求.生物质作为一种新型能源,是世界第四大能源,热分解、气化和燃烧是生物质能量转换的主要技术[1].传统的生物质能源利用大都是进行直接燃烧以获取能量,其碳利用率不足15%,而生物质气化技术可实现其高效、清洁利用,开发该技术具有十分重要的现实意义和战略意义[2].

目前,生物质气化技术在常规循环流化床中有一些应用,其缺陷为:生成气中带出物较多、热值较低、碳回流难以控制和碳转化率较低.双循环流化床生物质气化技术是新型生物质利用技术,它将生物质的燃烧与气化分开[3],生物质在气化室中进行热解气化,未完全气化的半焦在燃烧室中燃烧放热,加热载体并产生过热蒸汽[4],热载体携带热量进入气化室,提供生物质气化需要的热量[5].该新技术增加了床料在床内的停留时间,提高了碳转化率,产生的可燃气具有低含氮量、高热值和低焦油含量的优点,国内外学者已经在进行相关的研究[6-8].

由于热态双循环流化床生物质气化装置中最复杂的传热传质过程发生在燃烧室内,笔者定义燃烧室内单位时间内通过提升管某截面的固体物料量为颗粒循环流率GS.双循环流化床生物质气化技术的关键是控制双循环流化床内的颗粒循环流率,GS越大两床之间温差越小,就能维持较高的气化室温度[9].提升管送风特性对颗粒循环流率有一定的影响,这些特性包括提升管流化风速、二次风量QS及二次风送风方式、二次风口高度和风口数量等,但目前相关课题的研究报道还很少.BP网络预测模型实现了输入到输出的映射,适合求解内部机制复杂的问题,并能够用于系统的运行控制.因此,笔者通过大量试验数据建立、训练并优化了基于LM优化算法的BP神经网络预测模型,并对提升管送风特性影响下的GS进行预测,且与试验结果进行对比.

1 试验系统

试验台主体由有机玻璃制成,包括提升管、旋风分离器、立管、气化室、返料管和辅助系统.试验台的装置示意图见图1.气化室内径为200 mm,高2 m,顶部设有加料口,以方便进行加料;立管内径50 mm;在立管上安装有蝶阀用来测量系统内的颗粒循环流率;提升管内径为75 mm,高6 m,在提升管下部不同高度用不同方式布置多层二次风口;返料管内径为30 mm,为了减少两床之间的串气,返料管安装角度为55°;提升管和气化室的送风由两台风机提供,风机型号9-26No5.6;用蝶阀控制空气流量,采用转子流量计测量空气流量.

试验物料为石英砂,筛选277～401μm的石英砂颗粒,颗粒球形度为0.73,颗粒密度为2650 kg/m3,堆积密度为1650 kg/m3;气化室静床高18 cm,返料管口距布风板8 cm,静床料埋管10 cm,以消除物料高度对GS的影响.

图1 双循环流化床试验装置示意图Fig.1 Ex perimental setup of the dual circulating fluidized bed

2 试验结果及分析

试验研究了提升管流化风速、二次风量、二次风送风方式、二次风口高度及风口数量对双循环流化床GS的影响.为使GS不受气化室参数影响且保证物料流化,设定气化室风速u1=1.41 m/s.

2.1 提升管流化风速的影响

颗粒循环流率随着提升管流化风速up的增大而增加,如图2所示.这是由于流化风速增加,提升管由密相区进入飞溅区的物料增加,到达二次风口以上的物料被及时带走,密相区颗粒浓度减小,对返料管返料阻力减小,单位时间参加循环的物料颗粒增多.

2.2 提升管二次风量的影响

试验发现,颗粒循环流率随二次风量QS增大而增加.二次风量对颗粒循环流率的影响见图3.增加送入提升管的风量,即增大QS,使提升管内的风速增大 ,能够到达二次风口以上的物料被及时带走,提升管内压力减小,物料运行阻力减小,物料运动加快,因此GS随着QS增大而增加.当提升管风速达到一定的值(QS=0.0208 m3/s)后,飞溅区颗粒浓度降低,提升管底部的孔隙率变化幅度减缓,两床间的压差变化也相对放缓,GS增加幅度也趋于平缓.

图2 提升管流化风速对颗粒循环流率的影响Fig.2 Effect of fluidized air velocity in riser on the solid circulation rate

图3 二次风量对颗粒循环流率的影响Fig.3 Effect of secondary air flow rate on the solid circulation rate

2.3 提升管二次风送风方式的影响

试验中设置了4种提升管的二次风送风方式,四口径向、四口切向和两口径向、两口切向,见图4.

图4 提升管二次风口的四种方式Fig.4 Four structures of secondary air tuyere for the riser

试验发现,当二次风径向送入提升管时颗粒循环流率比切向送入时大,如图5所示.

二次风切向送风循环流率较小的原因是:提升管内径较小,颗粒受离心力作用贴壁严重,壁面附近颗粒团聚加重,颗粒团加速较慢;轴向中心区域风速较高,但物料浓度低,壁面附近颗粒浓度虽然高,但风速较小,造成GS下降;边壁处颗粒受到的壁面摩擦力较大,颗粒上升需要克服的阻力明显增大.

图5 二次风送风方式对颗粒循环流率的影响Fig.5 Effect of secondary air supply mode on the solid circulation rate

2.4 提升管二次风口高度的影响

当提升管风速较低时,风口高度对颗粒循环流率影响不大,部分颗粒达不到快速流态化所需曳力,此时风速是颗粒循环流率的主要制约因素.当提升管风速逐渐增大时,风口以上颗粒所受的曳力迅速增大,达到快速流态化,但在二次风口以下位置风速较低,到达二次风口以上的物料相对较少,此时二次风口高度成为颗粒循环流率的主要制约因素.因此,随着二次风量的增加,颗粒循环流率也增加,且幅度有增大的趋势,如图6所示.

图6 二次风口高度对颗粒循环流率的影响Fig.6 Effect of tuyere height on the solid circulation rate

2.5 风口数目的影响

提升管上布置4个二次风出口比布置2个二次风口时管内流场更均匀,具有更好的空气动力场,截面颗粒分布不均的状况有所改善,颗粒团聚现象减少.风口较少时,流场不均匀,随着风口的增加,提升管内流场趋于均匀,使得颗粒循环流率增加,如图7所示.

图7 风口数目对颗粒循环流率的影响Fig.7 Effect of tuyere number on the solid circulation rate

3 BP神经网络模型预测及结果分析

3.1 BP神经网络及LM算法简介

BP神经网络是一种多层前馈神经网络,包括输入层、隐含层和输出层,是利用非线性可微分函数进行权值训练的网络,其基本学习过程由信号的正向传播与误差的反向传播两个过程组成.预测值与真实值之间的误差从输出层经过隐含层逐层修正各连接权值,最后回到输入层,也叫“误差逆传播算法”[10],如图8所示.标准BP算法存在一些不足,如易形成局部极小而得不到全局最优;训练次数多使得学习效率低,收敛速度慢[11].为了提高其性能,BP神经网络的改进主要有2种途径:一是采用启发式学习方法;二是采用更有效的优化算法.

图8 n个输入、1个输出、i个隐含层的BP神经网络Fig.8 Schematic diag ram of a BP neural network

LM(Levenberg-Marquardt)算法是梯度下降法和高斯-牛顿法的结合,既有高斯-牛顿算法的快速收敛特性又有梯度下降法的全局特性,网络训练通过不断地调整权值及阈值来实现,可以有效地改善网络收敛性能[12].其基本思想是:为了减轻非最优点的奇异问题,使目标函数在接近最优点时,极值点附近的特性近似二次性,以加快寻优收敛过程[13],同时在梯度下降法和高斯-牛顿法之间通过自适应调整来优化网络权值,这大大提高了网络的收敛速度和泛化能力[14].其权值调整公式为:

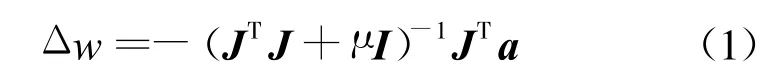
式中:a为误差向量;J为误差对权值微分的雅可比矩阵;I为单位矩阵;μ为标量,当 μ较大时,LM 算法接近于具有较小学习速率的梯度下降法,当μ=0时,该算法成为高斯-牛顿法.

3.2 BP神经网络模型结构设计及预测结果分析

隐含层数和隐含层节点数会影响网络性能.隐含层节点数量太少,网络从样本中获取信息的能力就差;隐含层节点数量过多,网络可能会记住样本中的噪声,降低泛化能力,训练时间增加.隐含层存在一个最佳神经元节点数,确定该节点数一般采用试凑法.根据 Kolmogorov定理,三层网络中输入、输出层节点数与隐含层节点数之间的近似关系为:

式中:m为隐含层节点数;n、l分别为输入、输出层节点数;α为1～10的常数.

本研究中测试得到的隐含层节点数为3～15,隐含层数取1和2.对比不同BP神经网络输出结果,认为输出值与实测值的误差和训练次数均较小的网络最佳.

利用基于 Levenberg-Marquardt优化算法的BP神经网络预测模型对双循环流化床颗粒循环流率进行了预测研究.BP神经网络选取试验部分的前4个影响因素作为输入层:提升管流化风速、二次风量、二次风送风方式和二次风口高度;输出是颗粒循环流率GS.从96组试验数据中随机选取80组作为训练样本,其余作为测试样本.为了使样本所有分量在网格训练时同等重要,先对训练样本和测试样本进行归一化处理.

BP神经网络输入层到隐含层传递函数选用双曲正切S型传递函数“tansig”.S型函数具有良好的非线性特点且目标向量经过归一化正好满足函数tansig的输出要求.隐含层到输出层函数选取纯线性函数“purelin”.采用 Levenberg-Marquardt算法对模型进行训练.对不同隐含层、不同节点时的预测结果进行对比分析,如图9、图10所示.

算法中学习率设为0.1,学习率增加因子和下降因子分别为1.05和0.7,Marquart调整参数初值m=0.01,其上升因子和下降因子分别为0.1和10,m最大值为1×105,训练次数为100次,目标误差为0.001.

观察模拟结果发现:BP神经网络隐含层有6个节点时,预测结果相对误差较小,1个隐含层时最大相对误差为1.016%,2个隐含层时最大相对误差为0.916%,二者均较准确;但2个隐含层时训练次数是1个隐含层时的2倍.所以可认为含1个隐含层、6个节点时的神经网络为最佳网络,该BP网络预测结果如图11所示.

图9 3层、4层网络最大相对误差对比Fig.9 Comparison of maximum relative error between layer 3 and layer 4

图10 3层、4层网络训练次数对比Fig.10 Relative prediction error of the optimal BP neural network

图11 最优BP神经网络预测相对误差Fig.11 The relative prediction error of the optimization BP neural network

最优BP神经网络模型预测的平均偏差为0.07 kg/(m2◦s),平均相对误差为0.49%;第14个样本偏差最大,为0.23 kg/(m2◦s),该点相对误差为0.915%;第15个样本偏差为0.14 kg/(m2◦s),相对误差为1.016%.

4 结 论

(1)颗粒循环流率随着提升管流化风速和二次风量的增大而增加,且二次风量超过一定值后,增加的趋势变缓;径向引入的二次风比切向引入时的颗粒循环流率大;颗粒循环流率对二次风口高度的变化十分敏感,风口最佳高度的选取还有待研究.

(2)基于LM优化算法的BP神经网络预测模型能准确地预测双循环流化床的颗粒循环流率.当BP神经网络含有1个隐含层、6个节点时模型预测效果达到最佳,平均相对误差仅为0.07%,最大相对误差为1.016%,能够准确地预测提升管送风特性对颗粒循环流率的影响,对双循环流化床的运行控制有一定意义.

[1]PRIYANKA K,TOBIAS P,HERMANN H.Model for biomass char combustion in the riser of a dual fluidized bed gasification unit:partΙmodel development and sensitivity analysis[J].Fuel Processing Technology,2008,89:651-659.

[2]吴晓江,张孝忠,朴桂林,等.高温加压气流床内生物质气化特性的实验研究[J].动力工程,2007,27(4):629-634.WU Xiaojiang,ZHANG Xiaozhong,PU Guilin,et al.Experimental study on biomass gasification characteristics in high-temperature pressurized entrained flow gasifers[J].Journal of Power Engineering,2007,27(4):629-634.

[3]沈来宏,肖军,高杨.串行流化床生物质催化制氢模拟研究[J].中国电机工程学报,2006,26(11):7-11.SHEN Laihong,XIAO Jun,GAO Yang.Simulation of hydrogen production from biomass catalytic gasification in interconnected fluidized beds[J].Proceedings of the CSEE,2006,26(11):7-11.

[4]HOFBAUER H.CFB-steam gasification[C]//14thEuropean Biomass Conference And Exhibition Biomass For Energy,Industry And Climate Protection.Paris:[s.n.],2005.

[5]LÖFFLER G,KAISER S,BOSCH K,et al.Hydrodynamics of a dual fluidized-bed gasifier part I:simulation of a riser with gas injection and diffuser[J].Chemical Engineering Science,2003,58(18):4197-4213.

[6]王立群,宋旭,周浩生,等.在流化床气化炉中生物质与煤共气化研究(Ⅱ)[J].太阳能学报,2008,29(3):354-359.WANG Liqun,SONG Xu,ZHOU Haosheng,et al.Development study on co-gasification of biomass and coal in fluidized bed gasifier(Ⅱ)[J].Acta Energiae Solaris Sinica,2008,29(3):354-359.

[7]高杨,肖军,沈来宏.串行流化床生物质气化制取富氢气体模拟研究[J].太阳能学报,2008,29(7):894-898.GAO Yang,XIAO Jun,SHEN Laihong.Simulation of hydrogen production from biomass gasification in interconnected fluidized beds[J].Acta Energiae Solaris Sinica,2008,29(7):894-898.

[8]XU G W,MURAKAMI T,SUDA T,et al.Twostage dual fluidized bed gasification:its conception and application to biomass[J].Fuel ProcessingTechnology,2009,90(1):137-144.

[9]陈鸿伟,刘焕志,李晓伟,等.双循环流化床颗粒循环流率实验与BP神经网络预测[J].中国电机工程学报,2010,30(32):25-29.CHEN Hongwei,LIU Huanzhi,LI Xiaowei,et al.Experimental research on solids circulation rate in a double fluidized bed and BP neural network prediction[J].Proceedings of the CSEE,2011,30(32):25-29.

[10]飞思科技产品研发中心.神经网络理论与 MATLAB7实现应用[M].北京:电子工业出版社,2005:99-108.

[11]周开利,康耀红.神经网络模型及其MATLAB仿真程序设计[M].北京:清华大学出版社,2005:69-90.

[12]刘鹏.一种基于 Levenberg-M arquardt算法的神经PID控制研究[J].重庆工商大学学报:自然科学版,2008,25(2):139-142.LIU Peng.Research into neural network system PID controller based on Levenberg-Marquardt algorithm[J].Chongqing Technology Business Univ:Nat Sci Et,2008,25(2):139-142.

[13]胡洁,曾祥金.基于LM算法的BP神经网络股价预测[J].科技创业月刊,2007,20(2):183-199.HU Jie,ZENG Xiangjin.BP neural network stock prediction based on LM algorithm[J].Pioneering With Science&Technology Monthly,2007,20(2):183-199.

[14]赵弘,周瑞祥,林廷圻.基于 Levenberg-Marquardt算法的神经网络监督控制[J].西安交通大学学报,2002,36(5):523-527.ZHAO Hong,ZHOU Ruixiang,LIN Tingqi.Neural network supervised control based on Levenberg-Marquardt algorithm[J].Journal of Xi′an Jiaotong University,2002,36(5):523-527.