一种家庭安保机器人运动路径规划的蚁群算法*

龙 珑 ，邓 伟 ，胡秦斌 ，黄智海

(1.广西师范学院 计算机与信息学院,广西 南宁530023；2.广西肿瘤防治研究所，广西 南宁530021)

根据“十二五”国家发展规划，家庭信息数字化、全智能化将成为我国信息产业发展的重点，智能家庭安保机器人将作为一个新兴产业的重要分支出现。合理的运动路径规划是家庭安保机器人研发面临的难题之一，它具体指家庭安保机器人在有障碍物（包括椅子、柜子、冰箱等家具）的复杂家庭环境中，根据某些优化算法准则，能快速找出从起点到目标点最优的安全运动路径。本文的家庭安保机器人运动轨迹规划使用蚁群算法中群智能技术来解决这个难题。假如家庭安保机器人运动轨迹规划直接使用蚁群算法，会由于蚁群算法本身最优解和收敛速度慢的特点[1-4]，造成家庭安保机器人运动轨迹局部路径选取方法优而全局路径选取方案不是最好。而混沌恰恰相反，具有全局遍历性的特点，可以避免家庭安保机器人在搜索选取运动路径时陷入局部最优解，确保全局路径最优。与家庭安保机器人运动路径单独采用蚁群算法相比，混沌蚁群算法在家庭安保机器人在家庭复杂环境中搜索选取全局运动路径方面具有优势。

1 家庭安保机器人运动路径规划理论基础

混沌理论[5-8]是使用整体、连续的数据关系解释及预测探讨动态系统中无法用单一的数据关系与行为，如机器人搜索探知路线、化学物理实验、气候变化等属于混沌理论范畴。当物理系统行为接近实际而没有内在随机性的模型但具有貌似随机的行为，称此系统为混沌。所以混沌理论看起来状态是混沌的，是事实上内在结构却非常精致，具有全局性、随机性、遍历性及规律性等诸多特性，能在规定的范围内按已制定好的规则反复遍历搜索所在状态，直至达到最优的选择方案。如果在家庭安保机器人运动路径规划中利用混沌理论的全局和遍历等特性，可帮助家庭安保机器人在复杂的家庭环境中找到最佳的运动路径。

蚁群算法是意大利著名学者M.Dorigo受自然界蚁群外出觅食行为的启发提出的，然后提出算法思想模拟蚁群外出觅食运动过程实现寻优。这种算法是一种启发式算法，此后很多学者对蚁群算法不断进行改进和深化，使得这种算法帮助人们解决了大量的实际问题。蚁群捕食初始阶段，利用混沌运动的遍历特性先进行全局混沌初始化搜索；在给出一点启发信息条件下每个混沌量对应一条运动路径，选择并记录下比较好的运动路径，留下这些运动路径的信息素；最后，蚂蚁再从这些比较好的运动路径中选择最佳的运动路径。整个过程数学建模工程认为有x只蚂蚁放在一个二维空间R中，蚁群最小化的函数f，在二维空间R中的每个点d都是可以给出问题的可行解[9-12]。目前蚂蚁的位置、蚂蚁邻居的位置和蚁群组织变量的函数构成了每个蚂蚁的运动轨迹规划测量，而蚁群的组织变量控制整个蚁群对个体蚂蚁的影响。有了这样的理论基础，家庭安保机器人设计小组就可以把家庭安保机器人运动路径规划问题数学建模为带约束的优化问题。

2 家庭安保机器人运动路径规划数学建模

2.1 运动路径规划问题描述与家庭环境建模

家庭安保机器人运动路径规划问题的目的就是让家庭安保机器人能够在家庭复杂环境中从起始位置出发，安全快速地找到一条避障最短路径，从而达到目的位置。

为了便于表示家庭安保机器人运动路径规划蚁群算法，把家庭环境俯视图方法映射为二维空间，用(x，y)表示空间坐标，并做以下一些假设：家庭空间图为矩形，其中分布有一定数量的家具等障碍物；把家庭安保机器人看成质点(家庭安保机器人相对家具很小，可以看成是质点)，全部障碍物看成外切四边形的形状，如果不满一个网格点，就以一个网格计算，以此类推。

假设R为家庭安保机器人SRob(Security Robot)在二维家庭平面的运动区域。建立一个家庭平面直角坐标系，横向坐标为X轴，纵向坐标为Y轴，家庭平面图上在X、Y轴上的最大值为xm、ym，以家庭安保机器人平均步长λ为栅格四边形长和宽距离，然后把家庭平面图分为等间距的栅格图。家庭平面图上X轴上栅格数I=xm/λ，家庭平面图上 Y轴上栅格数J=ym/λ。在家庭平面图中障碍物赋值为0，自由栅格也赋予相应的序号数，在家庭平面图中栅格序号值坐标关系可以表示为：

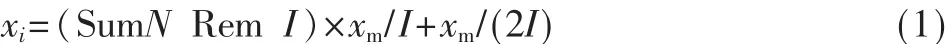
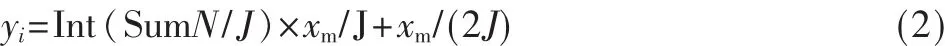
其中，Int为取整运算，Rem为求余运算，SumN总栅格数。家庭平面图所得坐标与序号的关系如图1所示。

图1中，家庭平面图任意两个栅格间距离长度表示为 L(di，dj)，d表示家庭平面图的可行节点。则

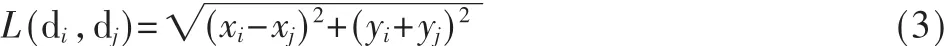
S为家庭安保机器人SRob在家庭平面图的行走步幅的取值范围，S={1,}，家庭安保机器人 SRob取值范围领域 SR(di(xi,yi))={d|L(d,di)≤S}，图 1中的粗实线表示以上情况的区域。可以得知在家庭平面图中的第n只蚂蚁的可行区Hi(n)=SRgi(k)-OBS-GriSn,其中OBS表示家庭平面图障碍物栅格的集合总数，GriSn表示家庭安保机器人在家庭平面度走过的栅格位置的集合。GriSn中在家庭平面图各个位置点的连线称为家庭安保机器人起始点dbegin到局部最优点的长度距离，记为D，有以下公式表示：

家庭安保机器人设计小组可以把家庭安保机器人在家庭复杂环境下的路径规划问题转化为带约束的优化问题，约束函数为D。

2.2 家庭安保机器人运动路径规划算法的模型

家庭安保机器人设计小组要把算法中单个蚂蚁的运动路径规划策略与蚂蚁所在的现在位置、局部最优解和组织变量做综合性考虑，以达到寻找全局最优的运动路径的目的。家庭安保机器人算法的蚂蚁i当前的位置是个体与群体的函数，表示为：

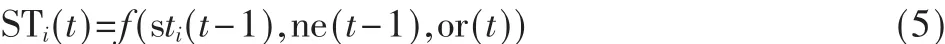
其中，STi(t)表示算法中第 i只蚂蚁的当前状态情况，ne(t-1)表示第i只蚂蚁与其邻居之间在t-1栅格内找到的最佳位置，or(t)表示这个系统的组织变量的当前状态情况。

家庭安保机器设计小组设第i只蚂蚁的固定邻居数目为3只，这只蚂蚁的邻居分别为第j只蚂蚁、第h只、第p只蚂蚁，它们在前面n-1次的迭代计算中的最佳位置是Ljbest、Lhbest、Lpbest,这些邻居蚂蚁的位置与信息都被传给第i只蚂蚁，这只蚂蚁根据自身的位置以及邻居蚂蚁的位置与信息，得出最佳的选择解。

把n只蚂蚁放到家庭平面二维空间中，蚁群之间的最小距离函数D，家庭平面二维空间的每个点d都是问题的可行解。当前蚂蚁的位置、蚂蚁邻居的位置和蚁群组织变量的函数构成了每个蚂蚁的运动轨迹规划测量，而蚁群的组织变量又可以控制整个蚁群对个体蚂蚁的影响，由此家庭安保机器人路径规划算法的优化系统模型可以表示为：

其中本家庭安保机器人的算法中实际应用时取0≤a≤2/3，b为相对足够大的数，在本家庭安保机器人的算法中实际取 b=300,组织因子Oi取 0～1之间，yi(0)=0.998。

2.3 家庭安保机器人运动路径规划算法实现流程

设计小组设dbegin为蚂蚁出发原点，dend为目标点，算法实现流程采用Sole的混沌系统流程，算法系统从开始就可以进行混沌搜索，算法实现流程如下：

(1)随机产生了起始原点 dbegin和起始终点 dend，所有参数被混沌初始化，记录和随时调整各蚂蚁行进路径的信息。

(2)系统为每个蚂蚁固定选取了3个邻居并做记录，开始时蚂蚁基本处在混沌搜索过程，每个蚂蚁从记录中搜索了解到邻居蚂蚁的最优位置和最佳行进路线，并以此为依据，取得下一步的行进路线。

(3)随着系统运行时间增长，组织变量也相应地会不断增大，家庭安保机器人运动轨迹算法中每个运动蚂蚁在组织变量的互相影响下，通过与其他邻居蚂蚁不断通信获得最佳的局部最优值，不断更新它们运动的方位，最后朝最优的位置移动，从而获得全局最佳解，也就是获得家庭安保机器人在家庭平面图的最佳的运动路径行进路线。

(4)假如算法中的蚁群全部收敛在一条运动路径上，则算法计算结束，并可以输出最佳的家庭安保机器人最佳运动路径图了，否则转向(3)继续运行。

3 家庭安保机器人运动路径规划算法仿真实验

为了验证算法的有效性，家庭安保机器人设计使用了如图2所示的模拟家庭环境地形进行仿真实验,其中黑色为家庭环境中障碍物格(包括家具、电器等)。家庭环境模拟地形图规模大约为蚂蚁数目的2倍左右，设计小组选取 n=20、组织因子 Oi=0.1+0.2α(其中 α为[0,1])、a=300、b=5/6、y(0)=0.998。 图 3 的仿真实验显示的是直接用蚁群算法的家庭安保机器人得到的结果，由于家庭安保机器人陷入了局部最优，无法得到最佳路径。图4的仿真实验显示本算法找到了最优的运动规划路径，这条路径安全规避障碍物，而且运动路径最短。仿真实验结果表明，增加了混沌理论的蚁群家庭安保机器人运动轨迹规划算法能有效避免陷入局部最优，机器人可以快速准确地在家庭复杂的环境中找到最佳的运动路径。

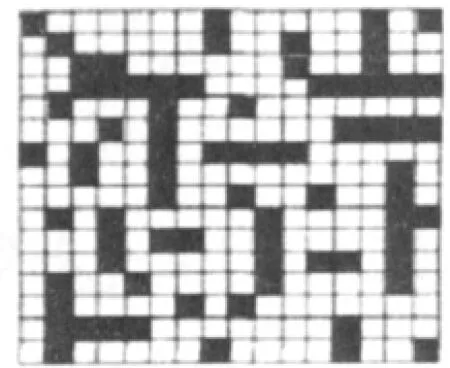
图2 家庭地形图

图3 直接蚁群算法得到路径图

图4 本算法得到路径图

家庭安保机器人在家庭复杂环境中的运动仅使用一般蚁群算法非常容易陷入局部最优，导致家庭安保机器人无法在家庭中找出最优运动路径。为此，本文将混沌理论引入蚁群算法中，利用混沌的遍历特性，为家庭安保机器人规划出一条局部趋势导航路径，运动路径在设定的组织因子的影响下动态地修改，加上在局部最优路径的互相影响引导下，不但成功避免了死锁、震荡，而且家庭安保机器人在家庭环境中的运动路径是最优的。从仿真实验可以看出，本算法具有简单、快速、实用性强等特点，家庭安保机器人使用本算法后能适应家庭复杂环境。进一步提高家庭安保机器人适应动态不确定环境下的运动规划能力是本课题下一步工作重点。

[1]BELLINGHAM J G,RAJAN K.Robotics in remoter hostitle[J].Science,2007(318)：1098-1102.

[2]赵小川,刘子峰,杨立辉.特种机器人运动轨迹规划及实现[J].计算机测量与控制,2011,19(8)：2024-2026.

[3]王华朋,钟雄虎.基于模糊化卡尔曼滤波的信息融合[J].计算机测量与控制,2006,14(8)：1230-1232.

[4]赵小川,罗庆生,韩宝玲.机器人多传感器信息融合研究综述[J].传感器与微系统,2008,26(8)：1-4.

[5]高玉华,苏剑波.JMF视频传输技术在Web机器人的应用[J].机 器 人 ,2004,25(3)：218-221.

[6]徐凯,冯瑞,董道国.基于 Web家庭安保机器人视频传输的研究与实现[J].计算机应用与实现,2011,28(8)：131-134.

[7]王箐华,崔世刚.应用几何理论的智能化机器人路径轨迹 仿 真 [J].计 算 机 仿 真,2010,27(3)：153-156.

[8]孙波,陈卫东.基于粒子群优化算法的移动机器人全局路径规划[J].控制与决策,2005,22(1)：12-16.

[9]刘召,陈恳.被动型机器人控制算法[J].清华大学学报,2010,50(2)：254-257.

[10]刘红霞,印文达,刘晓南.基于混沌蚁群算法的机器人路径规划[J].计算机测量与控制,2011,19(5)：1181-1183.

[11]左敏,曾广平.基于平行化的机器人智能控制研究[J].计算 机 仿 真 ,2011,28(8)：202-205.

[12]李丽香.一种新的基于蚂蚁混沌行为的群智能优化算法及其应用研究[D].北京：北京邮电大学,2008.