关联物流运输调度问题的改进遗传算法

汤雅连，蔡延光，赵学才

（广东工业大学 自动化学院，广东 广州 510006）

多车场多车型关联物流运输调度（RVRP）在现实生活中有很强的应用背景。针对多车场VRP问题，不少学者[1-4]已经做了很多研究，并取得了很好的成果，但是对于RVRP的探讨甚少。一般是若干个客户有一定的货物需求且货物之间有某种关联性，有多个车场为所有客户提供服务，车辆将货物送到各个客户地点，然后返回车场。由于车辆在行驶过程中，会受到路况[5]等因素的影响，所以本文主要考虑在路况约束下，对车辆和配送路线进行合理安排，满足所有客户要求的前提下，使配送成本最低。

1 问题描述及数学模型的建立

1.1 问题描述

道路容量约束的多车场、多车型关联物流运输调度问题简单描述为，假设给定车场信息以及客户信息（位置和货物需求量等），货物之间的关联系数，不同类型车辆信息（载重约束、里程约束和容量约束等），要求合理安排车辆和运输路线，在满足所有客户需求的前提下，使配送成本最低。

1.2 数学模型

有 l个客户（1，2，…，l），第 i个客户的需求量为 gi（i=1，2，…，l），需要从车场将货物运给客户，可派出载重为qh的货车，已知gi＜qh。客户要求送货的时间窗为[eti，lti]，每小时等待费用和延迟费用分别为 s1和 s2，早到或者晚到都会受到惩罚。Ti表示车辆到达i的时间。以表示车场 n中h类型的车辆k从i到j的运输成本（距离、费用、时间等），=。每种类型的车为Knh，客户 i，j之间的距离为 dij。rij表示 i货物与 j货物的关联系数。目标为考虑路况约束、载重约束、关联约束、多车场、多车型、软时间窗等情况下，使各车场的车辆能满足所有用户的需求，并使总运输成本最小。

假设客户编号为 1，2，…，l，车场编号为 l+1，l+2，…，l+N。定义变量如下：

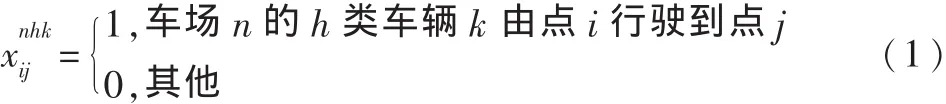
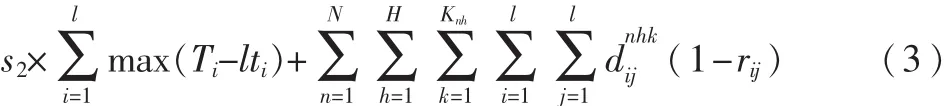
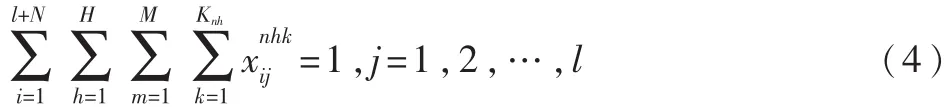
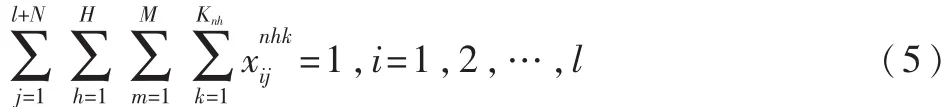
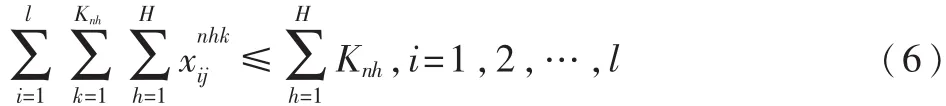
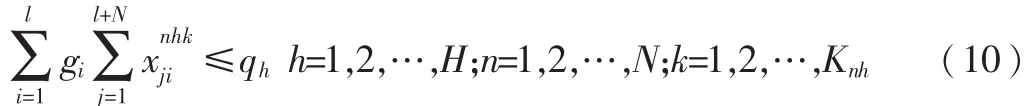
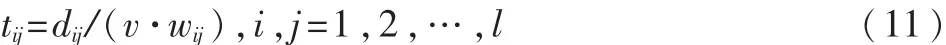
目标函数式（3）表示成本最低，以 cnijh表示n车场h类型的车辆从i点到j点的费用，rij表示货物之间关联度越高，兼容性越好，惩罚费用越低。式（4）、式（5）表示每个客户只能由一辆车服务；式（6）表示车场派出的车辆数不能超过该车场的车辆总数；式（7）表示 n车场 h类型车辆的里程约束；式（8）表示车辆必须回到原车场；式（9）表示不能从车场直接到车场；式（10）表示不能超过车辆载重限制；式（11）tij表示i到 j的行驶时间，wij为路段i与 j的路况系数，wij越大，说明路况越好，车辆行驶速度越快，时间越短；式（12）cs为单位配送费用。

2 算法设计

2.1 编码及初始种群的产生

本文采用参考文献[6]提出的编码方式及产生初始种群的方式。

2.2 适应度值计算与选择操作

fi=Z/Zi，即当前群体中最佳染色体的目标函数值z与当前染色体的目标函数值Zi的比值作为适应度值。根据轮盘赌策略，按适应度值的大小分配复制概率。

2.3 交叉

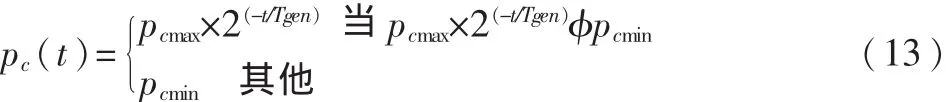
本节设计了与进化代数相关而与个体适应度无关的交叉概率计算公式（13）。t为当前进化代数，Tgen为预设的最大进化代数，pcmax为预设最大概率，pcmin为预设最小概率，pc（t）为当前种群的交叉概率。本文采取均匀交叉的方式。

2.4 变异

本文采用混沌变异策略，混沌变异形式如式（14）所示。 K（0，1）为（-2，2）按混沌规律变化的序列。

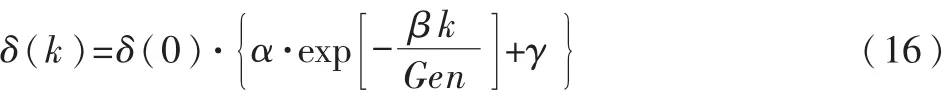
在进化初期采用逐渐缩小的变异尺度，利用参考文献[3]提出的变异策略，如式（16）所示。k为当前代数，Gen为最大迭代次数，δ为当前群体中某个体的某分量的变异尺度，α、β、γ为控制尺度收缩参数。

2.5 终止条件

当算法运行达到最大迭代次数或者多次产生同样的最优解，算法终止。

3 仿真分析

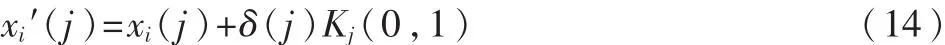
根据 Logistic映射[3]，如式（15）所示。 式中，u表示种群序号，u=0，1，…，n；β 表示混沌变量，0≤β≤1；μ 表示吸引子，当 μ 取 0～4时，Logistic映射为[0，1]间的不可逆映射，μ=4时，完全处于混沌的状态，此时产生的混沌变量 β（u）具有很好的遍历性。 β（u）经过放大和平移可得 K（0，1）。

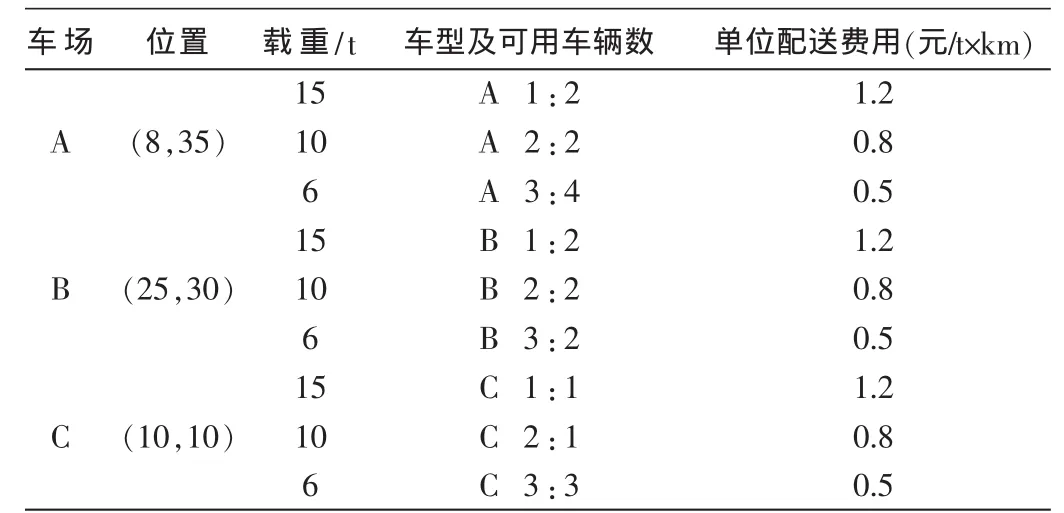
表1 车场位置信息

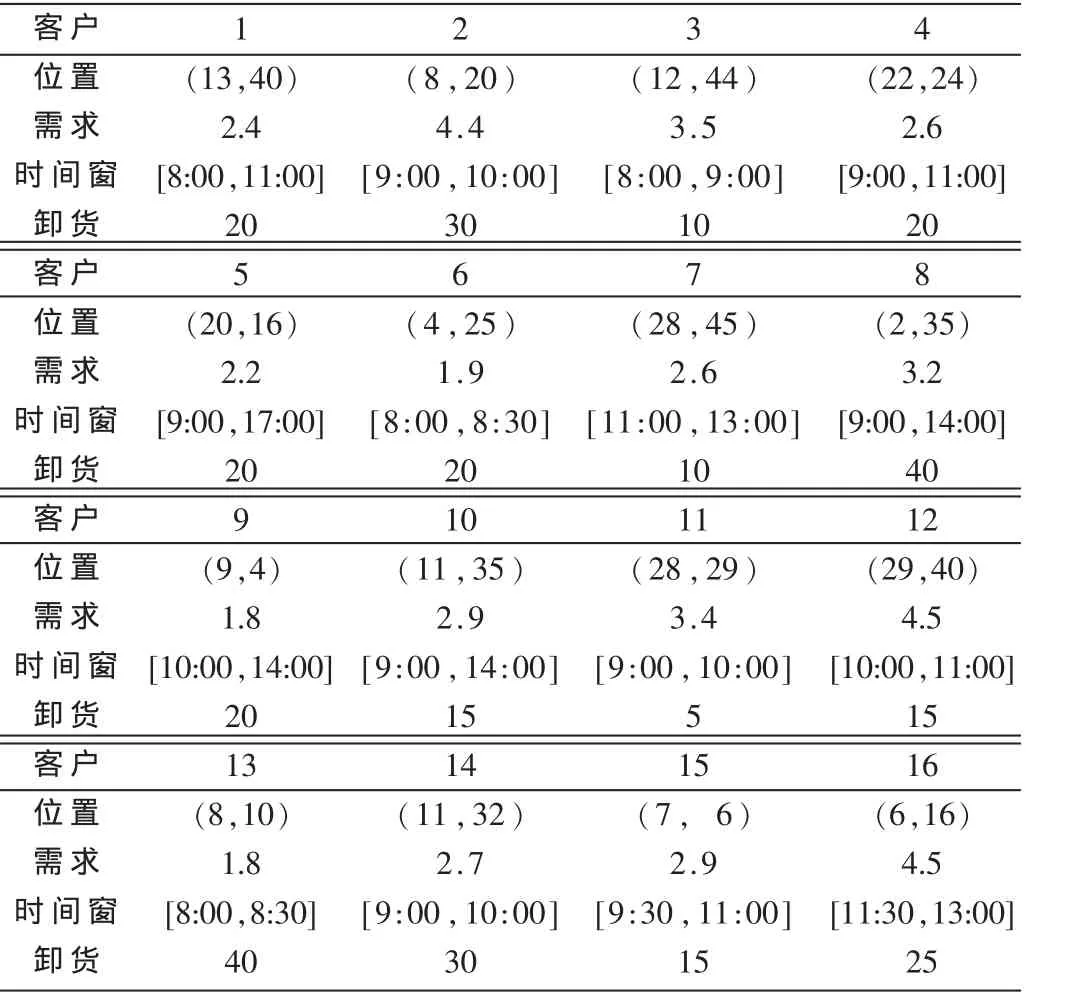
表2 客户信息

某供应处有3个车场，每个车场有不同类型的车辆，车场信息表见表1，客户信息表见表2。每辆车的正常行驶速度为60 km/h，最大配送里程为200 km。单位配送费用为 1元/t×km，等待费用为 10元/h，延迟费用为 100元/h。最早发车时间为 7：00。

本文中的实验是在 Intel（R）CoreTMi3 CPU2.53 GHz、内存2.0 GB的PC机上采用Microsoft Visual C++6.0编程实现。遗传算法中参数设置：种群规模为100，最大迭 代 次 数 Gen=100，pcmax=0.1，pcmin=0.005， 变 异 概 率0.05，尺度收缩参数为 α=1，β=10，γ=0.5，δ=0.5。运行程序20次，得到该算法求解本算例的最优结果见表3，配送示意图如图1所示。

表3 各配送车辆的配送数据

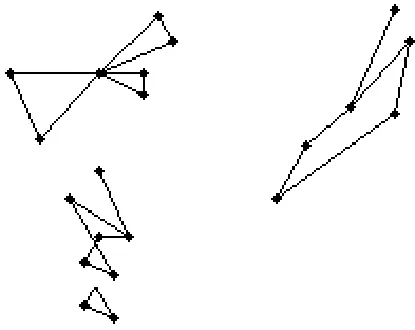
图1 配送路径示意图

本文考虑了收敛精度与进化代数的关系，混沌变异结合了“尺度收缩”思想，并采用了避免近亲繁殖的策略，达到了提高算法性能的效果。实验证明，改进的自适应混沌遗传算法求解此类问题是有效的。

[1]李臻，雷定猷.多车场车辆优化调度模型及算法[J].交通运输工程学报，2004，4（1）：83-86.

[2]李敏，郭强，刘红丽.多车场多配送中心的物流配送问题研究[J].计算机工程与应用，2007，43（8）：202-204.

[3]钟石泉，王雪莲.多车场集送一体化车辆调度问题及其遗传算法研究 [J].西安电子科技大学学报，2009，19（1）：63-68.

[4]YADLAPALLI S， BAE J， RATHINAM S，et al.Appriximation algorithms for a heterogeneous multiple depot hamiltonian path problem[C].2011 American Control Conference.2011.

[5]钟石泉，贺国光.单车场复杂情况下的车辆调度[J].系统工程，2005（5）：29-31.

[6]杨元峰.多车场多车型车辆路径问题的改进遗传算法 [J].计算机与现代化，2008（9）：10-12.