基于遗传优化的RBF-BP网络的实时故障检测

李仿华 ，王爱平 ，姚丽娜 ，国玮玮 ，徐晓燕

(1.安徽大学 计算机科学与技术学院，安徽 合肥230039；2.郑州大学 电气工程学院，河南 郑州450001)

随着工业化程度的提高，工业过程对系统的安全性和可靠性的要求也越来越高。因此，对故障检测技术的研究也越来越重要。目前已形成了多种故障检测技术，如人工智能[1]、线性矩阵不等式[2]、小波分析[3]和专家系统等方法。由于神经网络具有在微观结构上模拟人的认识能力的优点，它通过模拟人的大脑结构的形象思维来解决实际问题，决策时依据的是经验，而不是一组规划，对于任意非线性系统都可以看作是由输入到输出的一个映射，而神经网络具有很好的函数逼近能力，如RBF神经网络[4]，所以基于神经网络的故障检测方法[5]是一种有效的手段。理论上分析，只要选择合适的网络拓扑结构和连接权值，多层前馈网络和RBF网络均可以逼近任意的非线性函数。但由于BP网络具有学习速度慢、易陷入局部最优等不足，而RBF网络具有学习快、能够避免陷入局部最优等优点，因此本文将两种单一网络相互结合构成一个网络，即 RBF-BP，且只考虑稳定状态下的故障检测。

1 RBF-BP网络模型

对于非线性系统：

其中 f(·)和 g(·)均为非线性函数，可以根据系统的输入X(t)和输出Y(t)在正常状态和N个可能的故障状态对神经网络进行训练，对于样本集合，输入 xi(xi∈Rl)和输出 yi(yi∈Rm)存在某一映射 g，使得：

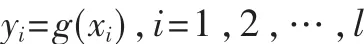
现要求得到某一映射h，在某种条件下，映射h是映射g的最佳逼近，神经网络就是一个最好的选择。利用BP等神经网络就能够实现对简单非线性函数的逼近，但是由于BP网络易陷入局部最优等不足，而对于RBF神经网络的非线映射能力主要体现在隐层基函数上，而基函数的特性主要由基函数的中心确定，从数据点中任意选取中心构造出来的RBF神经网络的性能同样不能令人满意，因此引入RBF-BP神经网络，结构如图1所示。

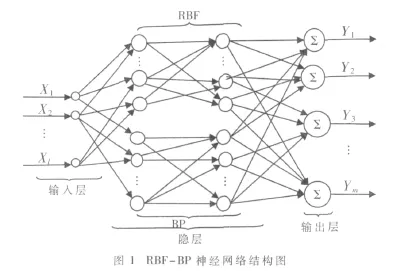
在该模型中，RBF-NN使用高斯函数为径向基函数，其具体形式为：

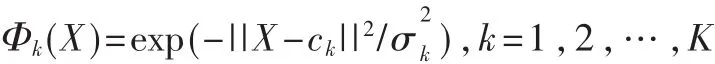
其中X为l维输入向量，ck为第 k个径向基函数的中心，与 X具有相同的维数，σk为第 k个隐层神经元的径向基函数宽度，||X-ck||2表示 X～ck之间的欧几里德范数，随着||X-ck||2的增大，Φk(X)会逐渐衰减，直至为 0，设隐层神经元的个数为K，则RBF-NN的网络输出为：

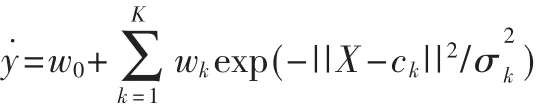
其中 w0为偏差，wk(k=1,2，…，K)为隐层到输出层的权值。

设BP-NN的网络输出为：

则记RBF-BPNN 的网络输出?为：

其中P和K为RBF-NN和BP-NN输出层的神经元个数。对于给定样本输入xi(xi∈Rl)和期望输出 di(di∈Rm)，定义输出误差 ε=di-y˜。

2 遗传优化的RBF-BPNN

为了解决神经网络结构设计和实时性差等问题，在对RBF-BPNN离线训练时，采用与遗传算法相结合的方式对网络的权值和阈值进行优化。通过对所有样本进行计算得到神经网络输出的均方误差，从而确定每个个体的适应度。经过若干代的计算，神经网络就会进化到全局最小，设误差函数为：

采用遗传算法对网络的训练实验结果如图2和图3所示。

3 实时故障检测

将训练好的RBF-BPNN按图4所示结构建立仿真模型。

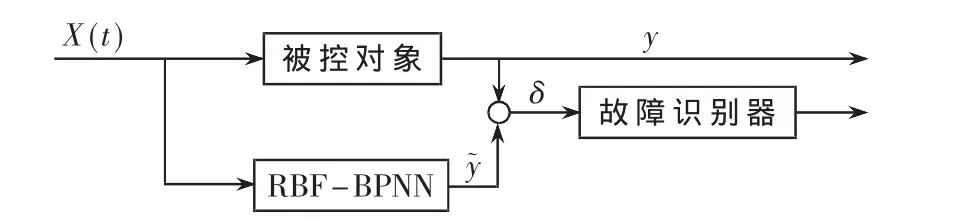
图4 RBF-BPNN系统结构图

其中δ为经过遗传算法优化的RBF-BPNN输出y˜与被控对象实际输出y的残差，当残差大于某一设定的阈值ξ时就认为被控对象发生了故障，这时故障识别仅需一个BP网络便可满足要求，下面是以东大智能多功能过程控制平台为实验平台，以温控、流速和液位控制作为被控对象进行实验，结果如下(故障类型设为DefaultType)：

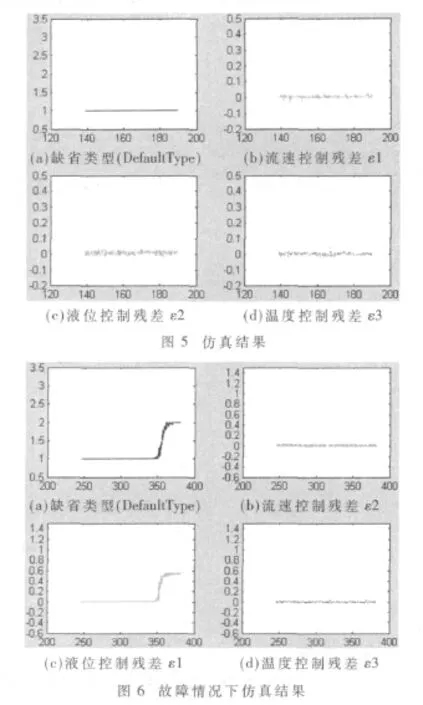
(1)当无故障发生时，系统残差 ε＜δ，此时将视残差信号作为噪声处理，实验结果如图5所示(系统正常时DefaultType输出为 1)。

(2)当系统发生故障时，即残差 ε>δ，不能简单地用消噪的方式消除，此时根据领域专家设定的阈值就可判断被控对象发生了故障，实验结果如图6、图7所示。

[1]YUSOF R，ZAFIRA R，RAHMAN A，et al.Fault detection and diagnosis for process control rig using artificial intelligent[J].ICIC Express Letters，2010，4(5B)：1811-1816.

[2]CHUGHTAI S S，Wang Hong.A high-integrity multivariable robust control with application to a process control rig[J].IEEE Transactions on Control Systems Technology，2007，15(4)：775-785.

[3]吴舰，吴楠.基于小波分析的煤矿机电设备故障检测关键技术应用研究[J].自动化与仪器仪表，2011(5)：83-89.

[4]柴杰，江青茵，曹志凯.RBF神经网络的函数逼近能力及其算法[J].模式识别与人工智能，2002，15(3)：310-316.

[5]Zhang Liang，LINDSAY B J，ASOKE K N.Fault detection using genetic programming[J].Systems and Signal Processing，2005(19)：271-289.