EXCEL在水文学线性回归分析中的应用

程冬梅，刘志峰，王琳琳

(1.宁阳县水务局，山东宁阳 271400;2.山东省水利工程管理局，济南 250013;3.山东省环境监测中心站，济南 250013)

0 前言

自然界中的许多变量，它们之间的关系可以概括为3种类型。第一种是确定性关系，即一个变量的值完全由另一个或另几个变量的值所决定;第二种是一个变量的取值与另一个变量的值毫无关系;第三种是一个变量的取值与另一个变量有一定的关系，它除受到另一个变量值的制约外，还受到其他变量的影响，因此它不完全由另一个变量确定。水文工作中所研究的变量，很多属于第三种关系，即相关关系［1］。相关关系虽然不是确定性的，但往往也存在一定规律，可以借助于数学工具，利用回归分析来研究符合这种相关关系的水文变量之间的变化趋势，并用函数来描述。

回归分析是水文学研究和实践中的极其重要的工具［1］。进行分析时，不但要建立回归方程，还要对回归方程进行显著性检验。在探求水文变量之间的关系时，往往这些变量是几十年的水文资料，数据十分繁杂，用人工计算既花费太多的时间，又很难保证精度要求，所以需要借助计算机来完成。如果只进行水文变量的线性回归分析，用微软公司office办公系统的EXCEL软件就可以达到目的，而且简单易用，只要有一点windows操作的经验，甚至不需要任何基础知识就可以在短时间内快速掌握其主要内容和基本操作，完成回归分析。

1 利用EXCEL进行一元线性回归分析

1.1 一元线性回归模型

水文学中有不少情况是用一元线性回归分析来解决的，其回归模型为

其中固定的未知参数β0，β1称为回归参数，变量x称为回归变量。

1.2 实现方法

通过例子［2］来阐述EXCEL求解方法。

例1数组(X)与数组(Y)的数据如下，试分析X与Y间的关系。

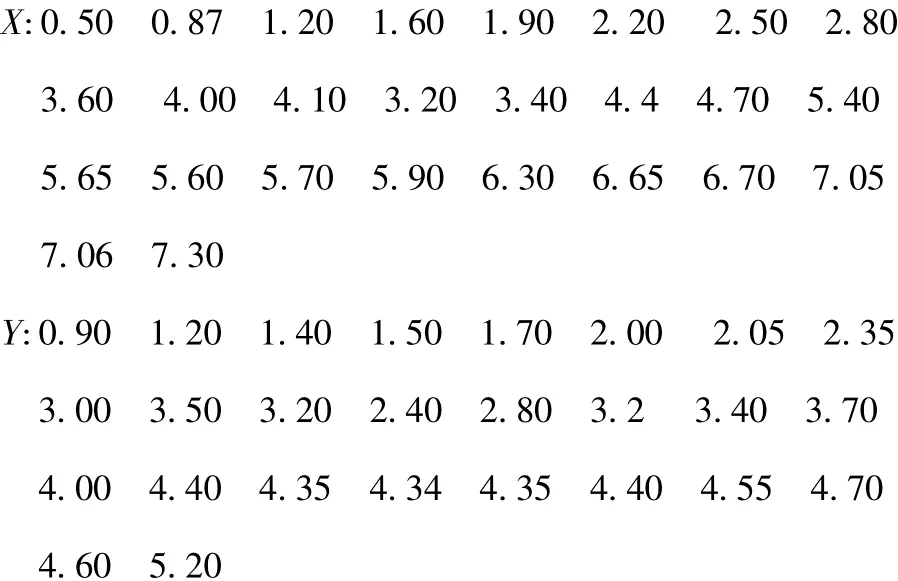
1)首先在Excel中建立工作表，样本X数据存放在A1:A27，其中A1存标记X;样本Y数据存放在B1:B27，其中B1存标记Y。

2)选取“工具”、“数据分析”…。

3)选定“回归”。

4)选择“确定”。

5)在“输入Y区域”框输入B1:B27。

6)在“输入X区域”框输入A1:A27。

7)关闭“常数为零”复选框，表示保留截距项，使其不为0。

8)打开“标记”复选框，表示有标记行。

9)打开“置信水平”复选框，并使其值为95%。

10)在“输出区域”框，确定单元格E2。

结果见图1所示，其中SS为平方和、MS表示均方、df为自由度。由此得到:

1)回归方程:Y=0.6754+0.5951 X;

2)F统计量的值:F=1107.942。由于P{F＞1107.942}=1.34353E－21(数值＜0.01为极显著;数值＜0.05、＞0.01为显著;数值＞0.05为不显著)，故所建回归方程极显著。

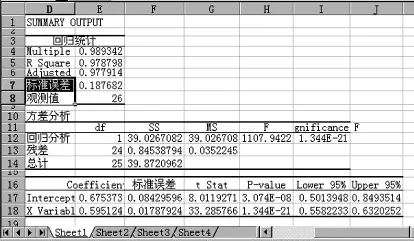
图1 利用EXCEL进行一元线性回归分析截图

2 利用EXCEL进行多元线性回归分析

2.1 多元线性回归模型

以二元线性回归分析问题为例进行说明，其回归模型为

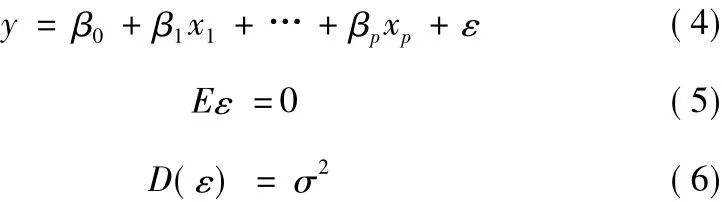
未知参数 β0，β1……，βp称为回归系数，变量 x1(i=1，……，p)称为回归因子。

2.2 实现方法

通过例子［2］来阐述EXCEL求解方法。

例2 数据如下所示，试分析X1，X2，X3，X4与Y之间的关系。

解 首先在Excel中建立工作表，其中样本X数据输入在A2:D16;样本Y数据输入在E2:E16。

①选取“工具”——“数据分析”。②选定“回归”。③选择“确定”。④在“输入Y区域”框输E2:E16。⑤在“输入X区域”框输入A2:D16。⑥关闭“常数为零”复选框，表示保留截距项，使其不为0。⑦关闭“标记”复选框。⑧打开“置信水平”复选框，并使其值为95%。⑨在“输出区域”框，确定单元格G1。

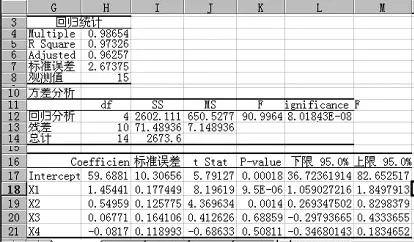
图2 利用EXCEL进行多元线性回归分析截图

由此得到:① 回归方程:Y=59.6881+1.45441X1+0.54959X2+0.06771X3－0.0817X4;②回归方程的显著性检验。

由于F统计量值为:F=90.9964，而P{F＞90.9964}=8.01843E－08(数值＜0.01为极显著;数值＜0.05＞0.01为显著;数值＞0.05为不显著)，故所建回归方程是极显著的;③回归系数的显著性检验:

关于X1，由于P{t＞8.196}=9.5E－6(数值 ＜0.01为极显著;数值＜0.05＞0.01为显著;数值＞0.05为不显著)，故X1是显著的;

关于X2，由于P{t＞4.369}=0.0014(情况同X1)，故X2是显著的;

关于X3，由于P{t＞0.413}=0.68896(情况同 X1)，故X3是不显著的;

关于X4，由于P{t＞－0.6863}=0.50811(情况同X1)，故X4是不显著的。

3 算例

现有河南省洛阳市瓦庙站和兴华站的年降雨量同步观测系列［3］，见表1。兴华站缺测1996年—1999年4年的年降雨量，要求建立两站年降雨量的回归方程，计算年初降雨量。

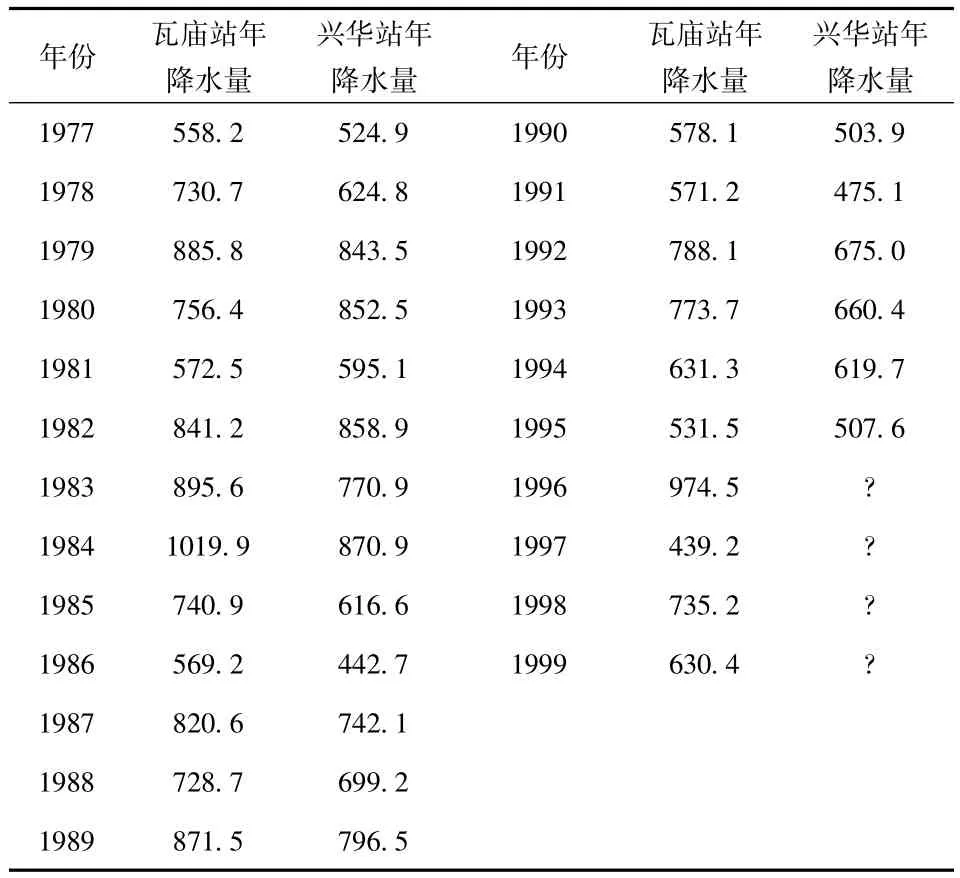
表1 瓦庙站、兴华站年降水量 /mm

设瓦庙站年降水量系列为 xi，兴华站年降水量系列为yi。

点汇两站年降水量的散点图发现，两变量的关系在图上呈直线趋势，故决定建立Y对X的回归直线方程，所以此类问题为一元线性回归分析问题。

试分析X与Y间的关系。

1)首先在Excel中建立工作表，样本X数据存放在A1:A20，其中A1存标记X;样本Y数据存放在B1:B20，其中B1存标记Y。

2)选取“工具”、“数据分析”…。

3)选定“回归”。

4)选择“确定”。

5)在“输入Y区域”框输入B1:B20。

6)在“输入X区域”框输入A1:A20。

7)关闭“常数为零”复选框，表示保留截距项，使其不为0。

8)打开“标记”复选框，表示有标记行。

9)打开“置信水平”复选框，并使其值为95%。

10)在“输出区域”框，确定单元格D23。

由此得到:

1)回归方程:Y=22.6660+0.8834 X;

2)F统计量的值:F=69.910。由于P{F＞69.910}=1.99018 E －07(数值＜0.01为极显著;数值＜0.05＞0.01为显著;数值＞0.05为不显著)，故所建回归方程显著。

3)由建立的回归方程可得兴华站1996年—1999年4 a的年降雨量(单位:mm)分别为 883.5、410.7、672.1、579.6。

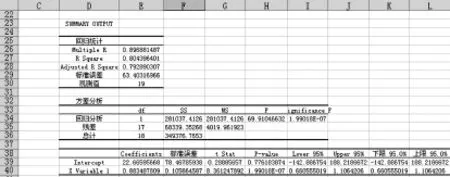
图3 利用EXCEL进行线性回归分析截图

4 结语

微软公司office办公系统的EXCEL软件功能十分强大，可以进行大量的数学运算。用它来解决水文学中的回归分析问题，既可以节约购买其它回归分析专业软件的花销，又可以提高运算效率，达到事半功倍的效果。

［1］黄振平.水文统计学［M］.南京:河海大学出版社，2003.

［2］李永乐，胡庆军.应用数理统计［M］.长沙:国防科技大学出版社，1995.

［3］叶守泽.水文水利计算［M］.北京:中国水利水电出版社，1992.