城市轨道交通双线桥上无缝线路挠曲力研究

王冬梅 倪向阳 王慧珺

(1.青岛理工大学汽车与交通学院 青岛 266033;2.青岛市地下铁道公司 青岛 266071)

高架桥作为地铁的一种线路敷设方式，其工程造价较低、施工速度快、适应线路线型的能力强，在国内外的地铁建设中发展很快并得到大量采用。在国外，如荷兰、法国、新加坡等地的地铁中都存在高架区段，国内北京、天津、上海、广州、深圳等城市也采用了部分高架线路。作为地面建筑，轨道交通高架桥不仅要满足轨道交通所需要的结构要求以及功能要求，同时也影响着行人的视线和感官。

在城市轨道交通高架桥上铺设了大量的无缝线路。由于高架线路桥梁结构的变化必然影响到无缝线路轨道结构的受力情况，因此，为了轨道交通在高架线路上安全平稳地运营，必然要对城市轨道交通桥上的无缝线路挠曲力做深入研究。

笔者针对双线U型梁和传统的双线箱型梁两种不同形式桥梁，建立了轨道-桥梁一体化力学有限元模型，并借用ANSYS有限元软件进行了钢轨受力、桥墩受力及桥梁挠度等方面的计算和分析，从而得出了两种形式双线桥梁的不同受力和变形，以便为今后城市轨道交通高架结构的桥型设计提供理论参考依据。

1 模型建立及参数选取

1.1 轨道-桥梁一体化模型的建立

要对梁轨相互作用进行有限元分析，必须建立适合有限元计算的梁轨相互作用模型。桥上无缝线路是一个非常复杂的力学系统，钢轨、桥梁、墩台和桥梁两端的轨道之间相互制约、相互协调，要进行精确的模拟是非常困难的，必须通过一定的简化处理。笔者将轨道、桥梁及其墩台作为一个整体来考虑，建立了桥上无缝线路纵向附加力的全桥有限元计算模型。这样可以比较全面地反映梁、轨间的相互作用，使计算结果更加准确，也更具实用价值。

根据梁轨相互作用原理，针对双线桥上无缝线路需要研究的问题，依据实际城市轨道交通中的北京某双线简支箱型和智利圣地亚哥4号线双线U型梁桥，建立如图1所示的力学分析模型。

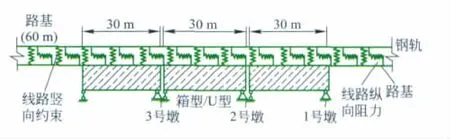
图1 双线简支箱型、U型梁桥无缝线路的力学分析模型

将钢轨视为连续弹性点支撑上的Bernoulli-Euler梁，以Beam188三维梁单元来模拟;线路纵向约束考虑成非线性弹簧-阻尼单元(Combin39);线路竖向约束、桥墩纵向约束均考虑成线性弹簧-阻尼单元(Combin14);混凝土桥梁以实体单元(Solid45)进行处理，选择使用正六面体网格并使用Ansys中的映射功能对实体进行单元划分。此外，在桥梁两端的路基上分别建立60 m的轨道结构，以满足边界条件的处理。

1.2 计算参数的选取

1)60 kg/m的钢轨。横截面面积77.45 cm2，竖向惯性矩3.217 ×10－5m4，水平惯性矩5.24 ×10－6m4，泊松比0.3，弹性模量 E 为2.06 ×1011 N/m2，密度 ρ为7830 kg/m3，热膨胀系数 11.8 ×10－6/℃。

2)钢轨扣件。竖向刚度为3.3×107N/m;桥上无砟轨道轨面无载时，纵向阻力取70 N/cm;轨面有载时，机车和车辆下纵向阻力取110 N/cm。

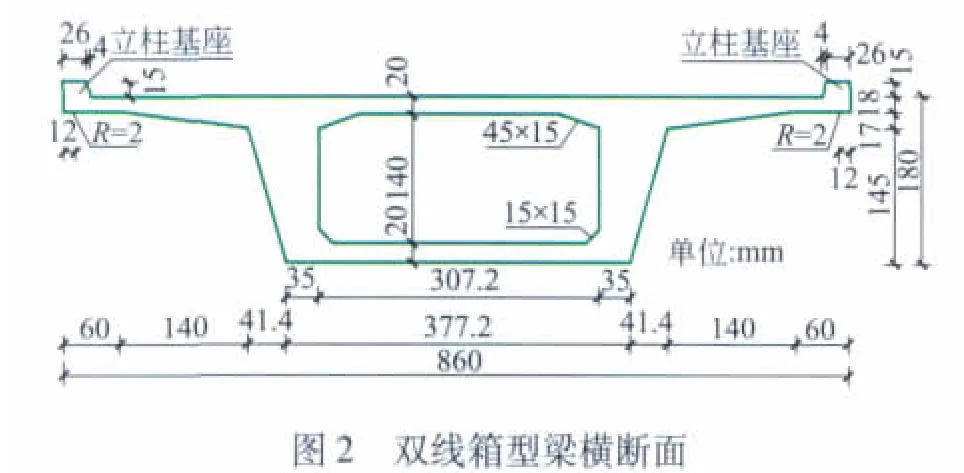
3)桥梁。双线30 m混凝土桥梁，断面采用当前某地铁线路已经应用的断面(见图2～图3)，泊松比0.2，弹性模量 E 为3.45 ×1010 N/m2，密度2500 kg/m3，热膨胀系数1 ×10－5/℃。

4)桥墩纵向水平刚度。我国GB 50157—2003《地铁设计规范》规定，采用无缝线路的区间简支梁高架结构桥墩墩顶纵向水平刚度应满足表1的要求，单线桥梁桥墩墩顶纵向水平刚度取表中值的1/2。

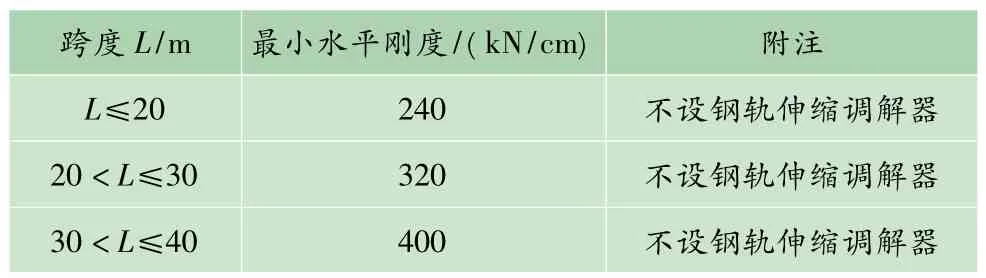
表1 桥墩墩顶纵向水平线刚度(双线)

桥墩纵向水平刚度选取320 kN/cm，竖向刚度取1000 kN/mm。

5)竖向荷载。为了简化计算，统一采用均布荷载进行研究。对于我国现状，计算荷载按大部分城市轨道线路所选的地铁B型车荷载，采用6节车辆编组，荷载长度为19.5 ×6=117 m，折合每延米轴重28.07 kN/m［1］。建成后的三维轨道-桥梁一体化模型如图4所示。

图4 轨道-桥梁一体化模型

2 桥上无缝线路挠曲附加力分析

当列车荷载进入桥梁上时，梁便产生纵向位移，梁位移带动轨枕、扣件位移，扣件对长钢轨施加纵向力会引起长钢轨变形，因而使梁轨间产生相对位移。梁轨互制而产生纵向力，称为挠曲附加力［2］。

通过对列车在桥上运行的所有工况进行分析，最不利荷载位置如图5所示。

图5 列车最不利荷载工况

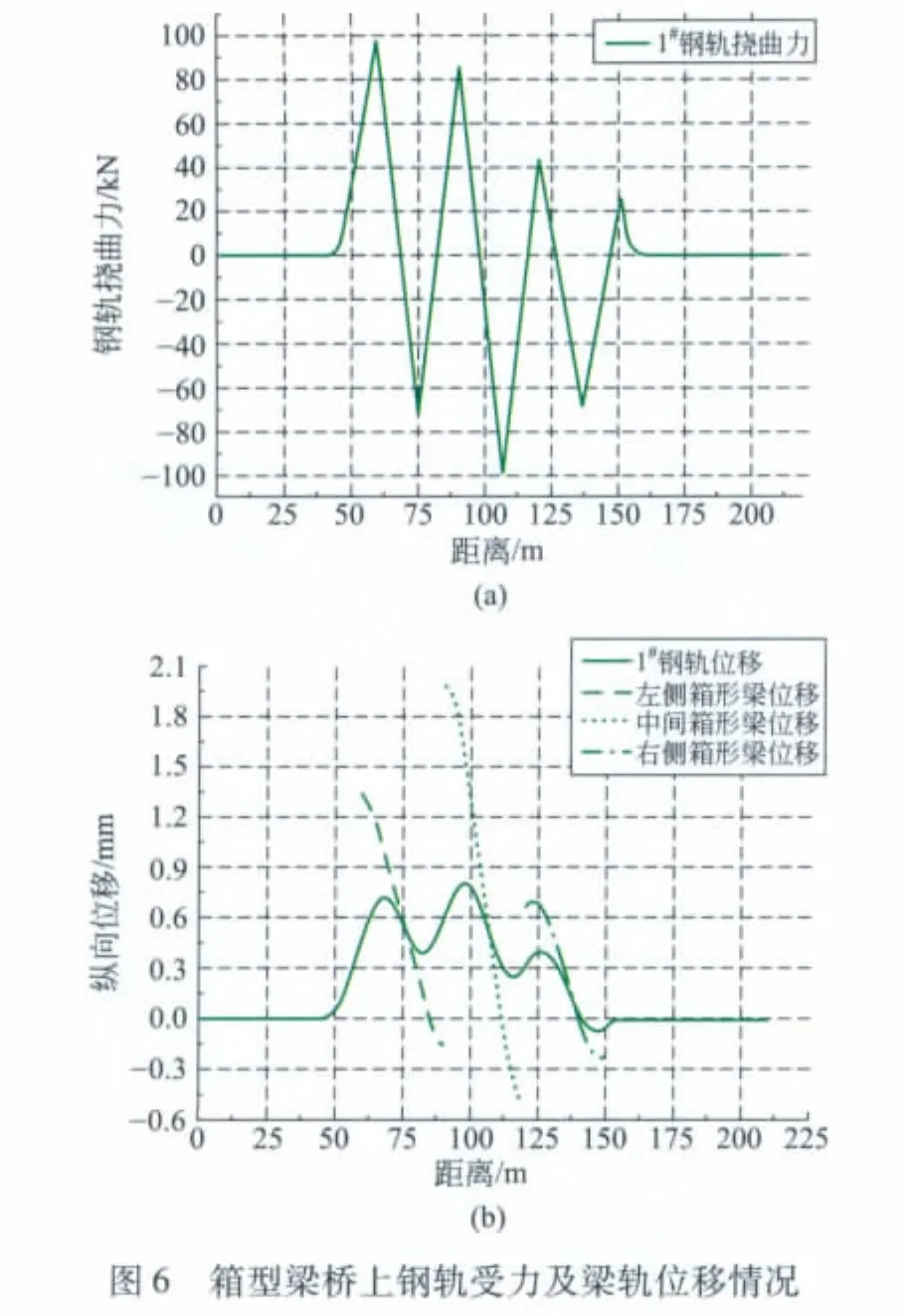
计算箱型梁在最不利荷载位置时的钢轨受力及其梁轨位移如图6所示，U型梁在最不利荷载位置时的钢轨受力及其梁轨位移如图7所示。

由图6可知，箱型梁的钢轨最大挠曲压力为99 kN，最大挠曲拉力为99 kN。此时，桥墩受力为111 kN，梁最大挠度为20.5 mm。

由图7可知，U型梁的钢轨最大挠曲压力为80 kN，最大挠曲拉力为61 kN。此时，桥墩受力为63 kN，梁最大挠度为17.1 mm。

3 附加挠曲力影响分析

前人的研究表明，影响桥上无缝线路挠曲力的因素包括线路的纵向阻力、桥梁的跨度和跨数、桥墩刚度及支座的布置、钢轨类型、运行工况等等，国内外已经进行了大量的研究。但是，对城市轨道交通桥上无缝线路的研究还不够深入，因此下面从线路纵向阻力、桥梁跨度和桥墩刚度等方面对挠曲力的影响做进一步研究。

3.1 线路纵向阻力对挠曲力的影响

3跨30 m双线简支梁桥，采用不同纵向阻力计算得到钢轨所受挠曲力的最大值和桥墩纵向力的最大值，如表2所示。

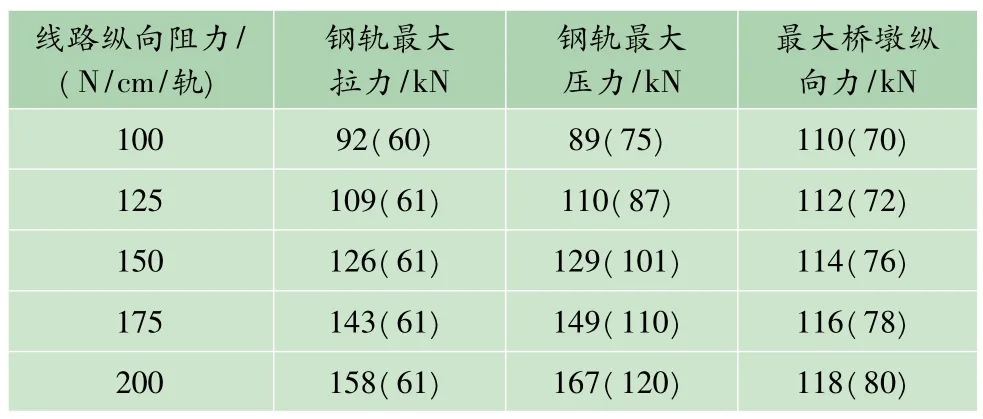
表2 不同线路纵向阻力对钢轨挠曲力的影响

由表2可知，改变线路纵向阻力时，箱型梁钢轨挠曲附加力变化幅度较大，桥墩受力变化幅度较小;U型梁钢轨挠曲附加压力变化幅度较大，挠曲附加拉力基本不变，桥墩受力变化幅度较小。

3.2 桥梁跨度对挠曲力的影响

就标准段高架桥来说，根据国内北京、上海、天津、广州、大连等城市已建成和正在建设的轨道交通高架桥来看，大多采用跨度长度为25、30或者35 m的梁。下面分别选取3跨25 m、3跨30 m、3跨35 m的3种简支梁进行分析，表3为采用不同桥梁跨度计算得到的钢轨所受挠曲力最大值和桥墩纵向力最大值。

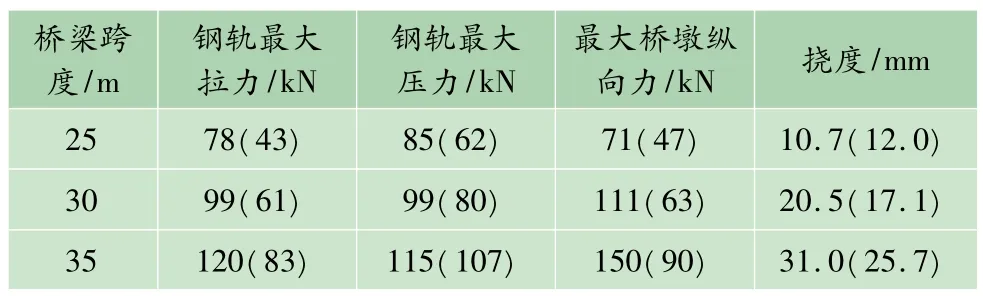
表3 不同桥梁跨度挠曲力的计算结果

由表3可知，当改变桥梁跨度时，箱型梁钢轨挠曲附加力变化幅度较大，桥墩受力变化幅度较大，挠度变化也较大;U型梁钢轨挠曲附加力变化幅度较大，桥墩受力变化幅度较小，挠度变化幅度也较小。

3.3 桥墩刚度对挠曲力的影响

由于桥梁墩台是桥梁结构的基础部分，支撑梁体及上部结构，是城市轨道交通桥梁的主要受力部件，也是影响钢轨纵向力的重要因素，因此在钢轨纵向附加力的计算中发挥重要作用。3跨30 m简支梁桥采用桥墩不同纵向刚度计算得到钢轨所受挠曲力最大值和桥墩纵向力最大值如表4所示。

表4 桥墩不同纵向刚度挠曲力的计算结果

由表4可知，当改变桥墩纵向刚度时，箱型梁钢轨挠曲附加力变化幅度较小，桥墩受力变化幅度较大;U型梁钢轨挠曲附加力变化幅度较小，桥墩受力变化幅度较大。

4 结论

1)双线简支梁桥钢轨挠曲力在加载区段很大，对无载区段影响很小，加载区段两端附近位置的钢轨力一般会出现峰值。箱型梁挠曲拉压应力相差不大，而U型梁的挠曲压力明显大于拉力。

2)双线U型梁钢轨挠曲力和桥墩受力均小于双线箱型梁，而U型梁桥梁挠度大于箱型梁。综合比较，双线U型梁受力性较好。

3)线路纵向阻力对钢轨挠曲力影响较大，而对桥墩受力影响较小;桥梁跨度对钢轨挠曲力影响较大，对桥墩受力以及桥梁挠度影响也较大;桥墩纵向刚度对钢轨挠曲力影响较小，而对桥墩受力影响较大。

［1］吴定俊.高架轻轨桥梁设计参数取值分析［J］.城市轨道交通研究.2002，5(2):37-40.

［2］卢耀荣.无缝线路研究与应用［M］.北京:中国铁道出版社，2004.

［3］闫子权，任兵杰，梁青槐.城轨U梁与箱梁桥上无缝线路受力及桥梁固有振动特性分析［J］.兰州交通大学学报，2011(1):54-58.

［4］蒋鹏.轨道交通槽型梁桥梁轨相互作用研究［D］.上海:同济大学，2008.

［5］卢耀荣，冯淑卿.桥上无缝线路挠曲力的计算［J］.铁道学报，1987，9(2):58-69.

［6］马坤全，沈钱斌，蒋鹏.城市轨道交通高架桥无缝线路梁轨相互作用研究［J］.城市轨道交通研究，2008，11(8):30-34.