相关干涉仪测向原始样本的求解方法

赵 地，任晓飞

（1.中国电子科技集团公司54所，石家庄050081；2.中国电波传播研究所，青岛266107）

0 引 言

传统的干涉仪测向体制虽然具有测向精度高、算法简单、实时性好等优点，但在工程应用中往往会受到以下问题的困扰：天线阵布局及应用环境的影响所产生的多径干扰问题；天线馈源设计原因引起的匹配网络的不一致、天线相位特性畸变等问题；多信道接收机信道的不均衡所引入的相位误差[1]以及相位解模糊等技术难点。

通过相关处理算法可以有效地弱化这些因素对测向精度的影响，相关处理算法的核心就是样本空间和代价函数的选择，但由于测向天线阵的体制和结构布局的变化，样本空间的求解也会随之不同。

1 相关干涉仪测向原理

1.1 相位差样本的定义描述

干涉仪测向的实质就是利用辐射信号在接收天线上形成的相位差来确定信号的来波方向。对于某一频率下来自θ方向的信号来波，以M元天线阵列中某一路接收到的相位为基准，其它路与基准路的相位差可假设为 （φ（1，0），φ（2，0），…，φ（M－1，0）），那 么如图1所示干涉仪测向原理图，通过天线阵布局的几何关系，可以得到如下对应关系：

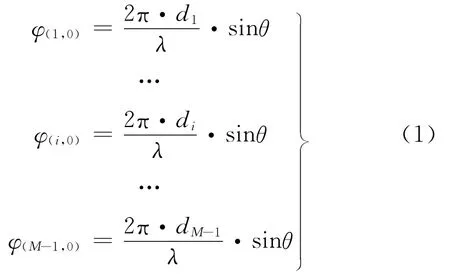
式中：di为基线长度；λ为入射信号的波长；θ为入射角；φ（i，0）为信号波前到达天线阵元0、i时的相位差。

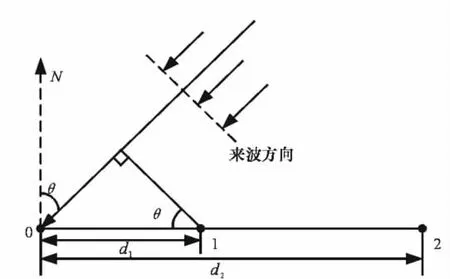
图1 干涉仪测向原理图

由公式（1）可以反推出：

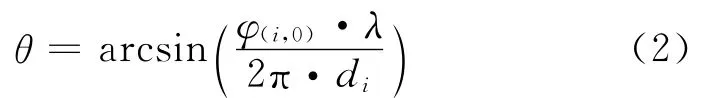
那么根据相位差φ（i，0）可以反推出方位角θ。由上述推导可知，在满足单值对应关系的条件下，信号方位 角θ和相位差向量 φ ＝ [φ（1，0），φ（2，0），…，φ（M－1，0）]之间存在着一种函数对应关系。若方位角θ以某一步进角度遍历360°，则可以得到若干对上述的对应关系Θ（θ，φ），这些方位角θ对应下的相位差向量φ即为原始相位差样本[2]。

1.2 目标函数模型

相关处理就是将天线阵列接收到的信号响应产生的观测样本与标准样本进行匹配运算的过程。由于相关干涉仪测向中的样本空间的标准样本一般是以信号相位差为测量变量的，因此，基于相位差拟合的相关干涉仪测向，其代价函数可表示为[3-4]：

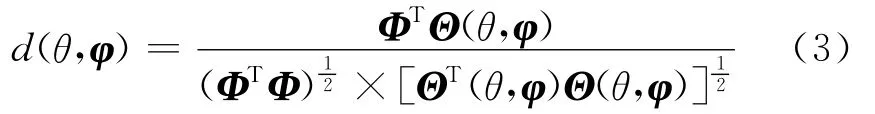
式中：Φ为某一固定频率下的观测相位差向量；Θ为干涉仪系统的原始相位差样本；φ为该频率下对应θ方向的相位差向量。

通过计算观测相位差向量与原始相位差样本间的相关系数并搜索峰值，找到所对应的空间信号来波方向。

2 原始相位差样本求解方法

对于一个空间信号来说，相关处理可以理解为该信号的相位差向量与空间滤波器的匹配运算[3]。因此，作为相关处理的匹配滤波器，原始相位差样本的质量对整个测向系统有着较为重要的影响。目前常用的原始相位差样本模型的求解主要通过以下几种方法推导实现。

2.1 阵列流形

以各向同性的M阵元全向天线组成的均匀圆阵为例，天线阵列的输出向量为[5]：

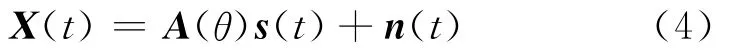
式中：A（θ）为阵列方向向量；s（t）为天线阵列接收到的窄带信号；n（t）为加性噪声。

其天线阵列布局如图2所示。

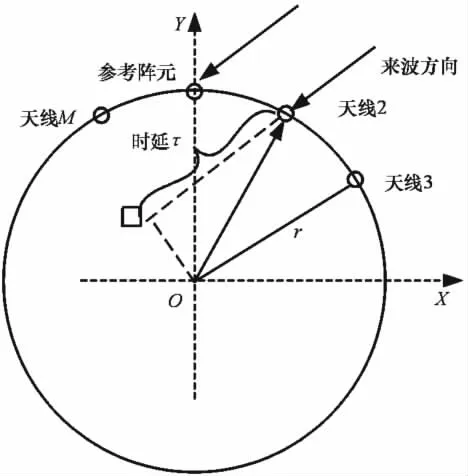
图2 天线阵列布局图

以圆阵中心为参考点，对于某一频率f和来波方向为θ的信号，可以得到该信号频率下天线阵列的输出向量，其频域下的输出向量为：

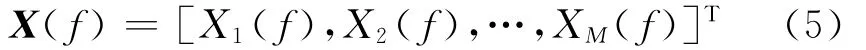
天线阵中某一阵元接收的信号响应[6]Xk（f）可表示为：

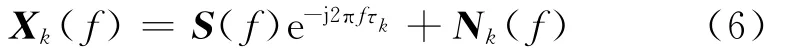
式中：τk为天线第k（k＝0，1，…，M－1）个天线阵元接收的信号相对于参考点的时延。

那么式（5）可以表示为：

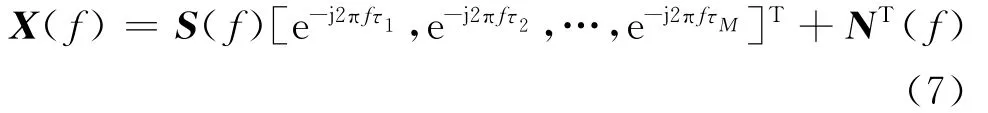
由于噪声频谱 Nk（f）与S（f）e－j2πfτk 的弱相关性，其相关系数为0。样本向量可以选择简化[4]为：

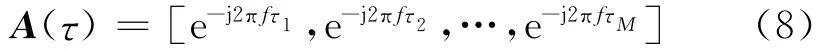
同时由上述均匀圆阵的天线布局，并且以圆阵中心为相位参考，可以计算出各阵元接收的信号相对于圆阵中心的信号时延τk所引起的相位值φk：

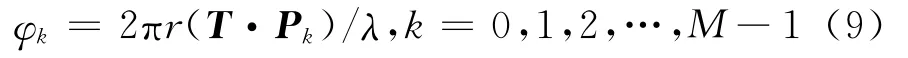
式中：T为来波方向的单位矢量；P为各个天线阵元的单位矢量。

信号时延τ最终是反映在天线阵列单元与参考点之间因波程差引起的相位差向量φ＝（φ1，φ2，…，φM－1）变化上。如果信号在0°～360°范围内以N个均分方位入射，则可以得到该模型下的样本Θ（θ，A（φ））。需要说明的是，该样本是一个以相位差向量φ为因变量的方向向量矩阵。该矩阵表示如下：

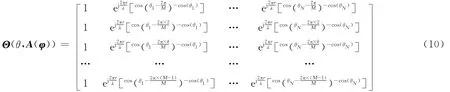
如果接收信号的各个通路幅相关系保持一致或者存在有源校准的情况下，利用天线阵列的方向向量作为原始相位差样本也是相关干涉仪测向的一个改进方法[6]。

2.2 天线响应

对于定向辐射天线组成的圆阵，以内向型对数周期天线为例，当测向天线的有效伸展宽度与信号波长之比大于1（大基础）时，通过阵列流形的推导得到原始相位差样本的方法就不适用了。

（1）测向天线的选择

由于定向天线有一定的辐射带宽，不具有完整的相位中心[7]，其相位中心随着工作频率及辐射角度变化，这就决定了在相关干涉仪测向体制下，由其组成的测向天线圆阵中，所有的阵元天线不可能都参与测向。一般选择入射信号落在天线等相面内的天线参与测向。图3所示为由定向天线组成的均匀圆阵方向图。

图中假设可参与测向的天线阵元个数为2 N＋1。根据对数周期天线相位中心计算公式[7]：

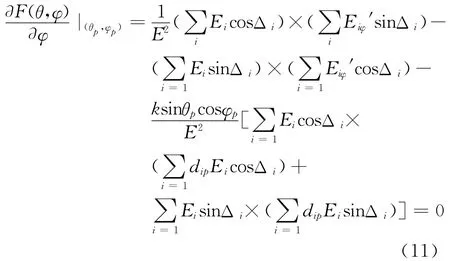
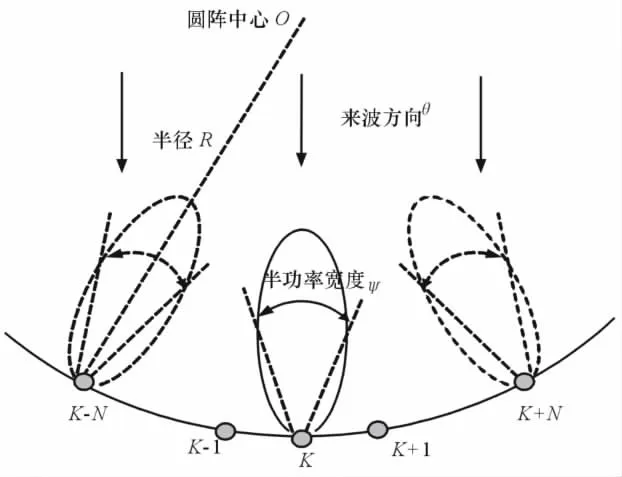
图3 定向天线阵方向图

通过数值计算得到具体某个阵元天线的相位中心，进而确定相位方向图。依据公式（11）对某对数周期天线进行仿真后得到的相位方向图如图4所示。

由图4可知，在方位角θ∈ [30°，150°]范围内天线具有较为一致的相位中心。据此根据M阵元均匀圆阵的天线布局，可以得到参与测向的天线个数为：2 N＋1＝θM／360°。

（2）原始相位样本的确定

原始相位样本主要取决于天线在远场区的电磁辐射特性。由于天线相位关系依赖于单元天线在阵列中的相对位置，因此分析相位时需要在阵列模型中统一分析单元天线相位特性，最终在处理原始相位样本时各个阵元相位都会基于相同相位归算点。以内向型对数周期天线圆形阵列为例，统一相位归算点一般都取圆心，各个阵元天线的相对位置都是以圆心为基准点。

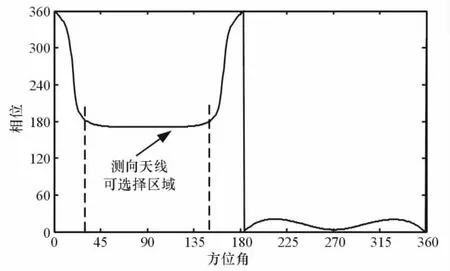
图4 对数周期天线相位方向图

对于一般自由空间中对数周期天线的响应特性，也就是天线的远场区电场辐射，有如下公式：

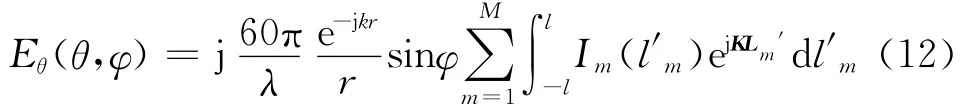
式中：Eθ（θ，φ）为电场在俯仰角φ上的场强分量；r为天线辐射源到空间某点的距离；k＝2π／λ，为波数；M为单个对数周期天线的振子数；Im为第m个振子上的感应电流；K为以波数为元素的矢量；Lm′为以l′m为元素构成的天线位置矢径 。

式（12）反映了天线在方位 和俯仰 上的响应特性。利用矩量法可计算出天线上的电流分布，代入（12）中得到天线远场电磁特性，进而得到天线远场幅度A和相位P的幅相关系，不妨用函数f（A，P，θ，φ）表示在某一固定频率f下该天线的这种响应关系。在确定参与测向的天线个数的基础上，将θ以固定角度τ等间隔取值（这里未考虑俯仰的响应关系），那么在测向波束范围内就得到若干组单个天线阵元的响应关系：

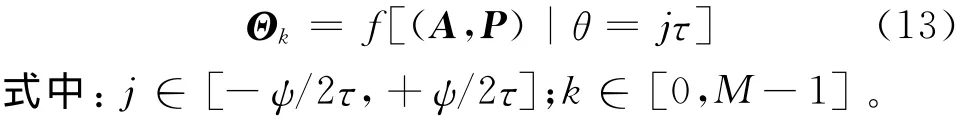
将单幅天线的幅相响应关系结合天线阵的位置信息，以及天线阵列结构的均匀性进行空间平滑，可以得到其他几路参与测向天线的幅相响应关系，从而得到原始相位差样本Θ。那么对应的原始相位差样本Θ可以表示为：

2.3 相关表采集

对于布局不规则的天线阵或测向天线阵受安装载体影响较大时，可采用相关表采集的方法。这种测向方法的基础是相位差数据的稳定性。同时，对于测向天线阵中的单独一副天线而言，还必须满足天线与电波传播理论中辐射远场的边界条件，即：

式中：L为接收天线与信号辐射源之间的距离；D为接收天线孔径的最大尺寸；λ为天线的工作波长。

实验证明，当接收天线与信号辐射源之间的距离大于L时，接收天线口径中心和边缘的相位差小于π／8，可以认为满足平面波入射的条件。

该方法主要通过采集源信号的相位信息，经过后处理后得到原始相位差样本。其实现步骤如下：

（1）用符合远场条件的源信号模拟外界信号，其频率范围为 [f0，fn]；

（2）源信号模拟频率范围 [f0，fn]内给定的某一频率为fi的信号，从某一固定方位θj入射后，采集天线阵各个阵元接收到的信号相位信息；

（3）以某一路为参考，各路相位作差并作解缠绕处理后，生成一组与入射方位θj和信号频率fi一一对应的相位差向量：

（4）以δ为频率步进，以γ为方位步进遍历0°～360°，得到若干组与入射方位γ×j和信号频率f0＋δ×i一一对应的相位差向量；

通过相关表采集得到的相关表矩阵反映了信号频率f0＋δ×i、入射方位γ×j和相位差向量φij三者之间的对应关系Θ（fi，θj，φij），该关系可用图5所示的矩阵形式表示。

图5 相关表矩阵关系图

图5中：r＝ （fn－f0）／δ；s＝360°／γ；i＝0，1，…r；j＝0，1，…s。

这里以一张二维矩阵的形式来描述相关干涉仪测向中原始相位差样本，它是以相位差向量为矩阵元素的。在误差范围内，若某一外界信号以某一未知方位入射，其产生的相位差向量就会真实地再现表内某一方位对应的相位差数据。

3 结束语

通过对上述几种求解方法的阐述，结合工程实际对这几种方法的适用条件和特征进行总结。

（1）从相关干涉仪测向的目标函数模型中，可以看到原始相位差样本对算法的精度和速度有较为重要的影响。样本计算的步进越小，相关系数的匹配精度就越高，但峰值搜索的时间就会相应地增长。

（2）基于阵列流形的推导方法，得到相关计算的匹配样本实际上是一个方向向量矩阵，它与原始相位差样本是一种复数幂的关系。通过天线响应数值仿真的方法，主要是对天线的频率响应做数值分析，进而得到天线的相位和幅度信息，以此作为目标函数的匹配样本。这2种方法得到的样本都是理论仿真数据，而通过相关表采集得到的原始相位差样本则真实地反映了天线在实际环境中的工作情况。（3）相关表采集的方法不受测向天线阵列布局的影响，而基于阵列流形的推导方法受天线阵列布局的影响较大。通过对天线的数值仿真求得响应关系，进而得到原始相位差样本的方法，需要对天线的设计和结构参数有比较深入的了解。

[1]张文旭，司锡才，蒋伊琳.相位干涉仪测向系统相位误差研 究 [J].系 统 工 程 与电 子 技 术，2006，28（11）：1631－1632.

[2]刘芬，明望，陶松.相关处理在干涉仪测向中的应用[J].电子科学技术评论，2005，16（6）：31－33.

[3]朱旭东.相关处理在干涉测向仪中的应用[J].现代雷达，2003，25（1）：22－25.

[4]李淳，廖桂生，李艳斌.改进的相关干涉仪测向处理方法.西安电子科技大学学报，2006，33（3）：400－403.

[5]赵地.均匀圆阵中的波束合成技术[J].无线电工程，2012，42（9）：32－33.

[6]韩广，王斌，王大磊.基于FPGA的相关干涉仪算法的研究与实现[J].电子技术应用，2010，36（7）：76－80.

[7]金元松，任晓飞，冀海鸣，等.对数周期偶极子天线全空间可变相位中心[J].电波科学学报，2007，22（2）：229－233.