基于ANSYS的架空输电导线找形研究

张旺海，于建斌

(华北电力大学机械工程系，河北省 保定市，071003)

0 引言

我国经济的快速发展对我国的电力建设提出了更高的要求，电网的建设和改造是电力事业面临的首要任务。架空输电线路是电网的主要组成部分，也是线路建设中的主要元件［1］，因此，对输电导线进行各种力学分析计算是线路安全的重要保证，也是进行线路设计的理论依据。在ANSYS中，对架空输电导线进行找形是导线动力分析的前提，有必要对找形方法进行研究。

1 导线找形的解析法

1.1 架空导线力学计算方法

架空线是悬挂在输电线路2个杆塔之间工作，由于2个杆塔间的距离较大，使得架空线的刚度对悬垂状态的影响相对变小，因此，在输电线路架线工程计算中经常忽略架空线的刚度，而视架空线为一柔索［2］。柔索的理论计算一般采用2个基本假定［3］:(1)索为理想柔性的，即不能受压也不能抗弯。(2)索的材料符合胡克定律。

架空线力学计算的基本方法有抛物线法和悬链线法［4］。

抛物线法认为架空线本身的单位长度自重力是按2悬挂点连线方向均匀分布的，按照此原则推导得到的架空线悬垂函数是抛物线型的［4］。所以按架空线单位长度自重力沿两悬挂点连线方向均匀分布的原则计算架空线弧垂、线长和张力的方法简称为抛物线法。

实际上架空线的自重力是按其本身线向均匀分布的，所以在理论计算中考虑架空线单位长度的自重力按线向分布才最符合实际。由此推导得到的架空线悬垂函数是悬链线型的，因此按照该原则计算架空线弧垂和张力等参数的方法称为悬链线法［4］。

显然悬链线法的计算精度比抛物线法的计算精度要高，但是其含有双曲线函数，计算比较繁杂。当垂跨比小于0.1时，抛物线法已经具有较好的计算精度，因此在工程上常使用抛物线法进行计算。工程中在高差系数较大的情况下，一般使用斜抛物线公式;高差系数较小时使用平抛物线公式进行计算。下面对悬链线法做简要介绍。

1.2 架空线的悬垂函数

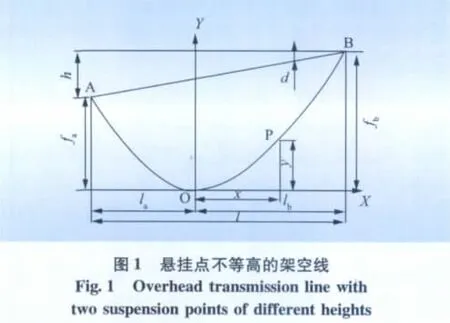
如图1所示，A、B是不等高的2个悬挂点，两者之间悬挂1条架空线，P为线上某任意点，O为架空线的最低点，取O为直角坐标系的原点。设架空线单位长度自重力ω是沿线向均匀分布的。取架空线OP线段为分析对象，由图2可知该线段在力矩Tp、H和Lxω这3者的作用下处于平衡状态。P点的受力矢量图如图2(b)所示。

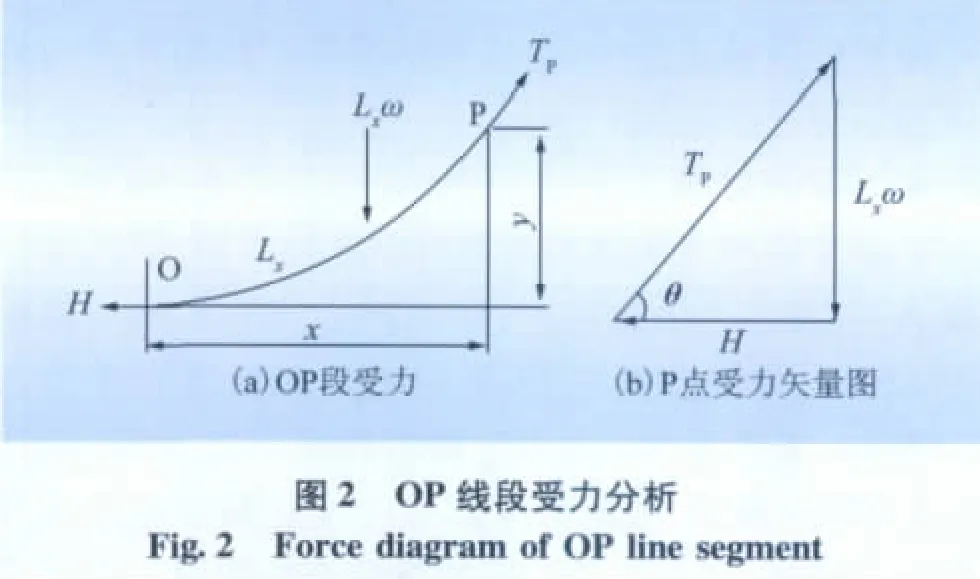
由图2可知

式中:H为架空线最低点的水平张力，N;ω为架空线单位长度的自重力，N/m。

两边同时求导

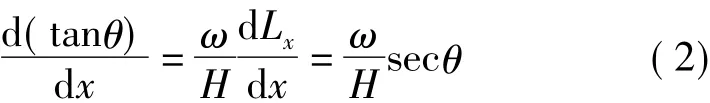
式中:x为架空线OP段任意点P对OP段最低点的水平距离，m。则

代入已知条件 x=0，tanθ=0，得 C1=0，所以有

即

式中:y为架空线OP段任意点P对线OP段最低点的高度，m。

整理并积分可得

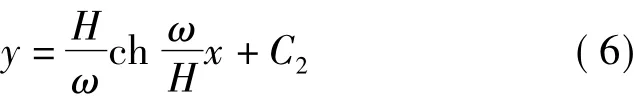
式(7)就是以架空线最低点O为直角坐标系原点的架空线悬垂函数式，为一悬链线函数，说明2个悬挂点间架空线的实际悬垂形状是悬链线型的。

1.3 架空线的弧垂

架空线某点的弧垂，是指从架空线上的该点到2个悬挂点连线的垂直距离，通过推导弧垂公式可以找出架空线的最大弧垂所处位置。

由式(7)得，当x=-la时有

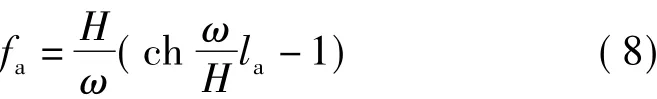
当x=-lb时有

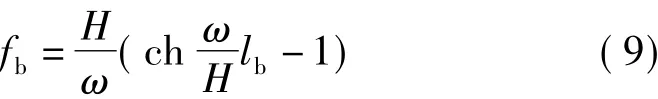
由h=fb-fa和l=la+lb，即可求得fa与 fb的表达式。

整理可得架空线各点的弧垂公式，再通过作图法找到架空线上的最大弧垂点，其最大弧垂值为

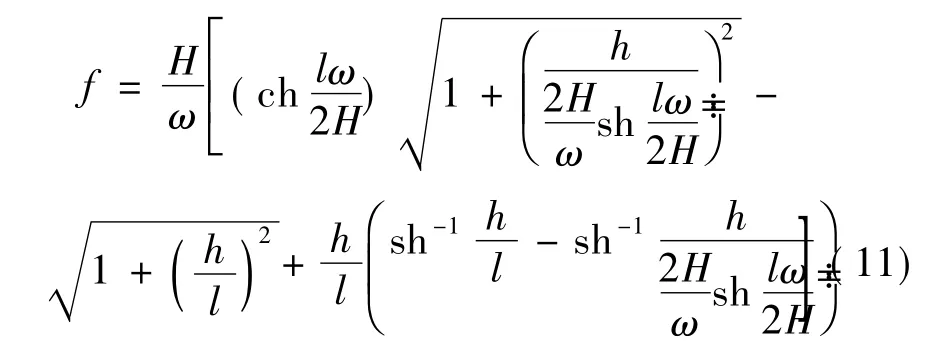
1.4 架空线的张力

由任意点的力三角形知，各点的轴向张力为

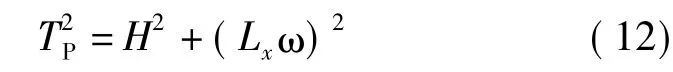
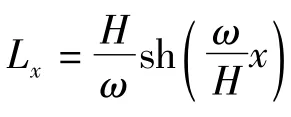
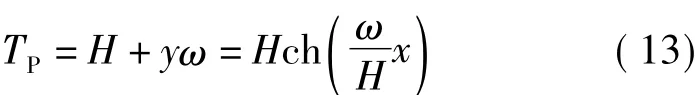
根据上式可以看出，架空线各点轴向张力T的水平分量相等，等于架空线最低点的水平张力H［5］;但是架空线各点轴向张力T的垂直分量不同，等于各点与最低点间弧段的垂直重力Lxω，故架空线最低点轴向张力的垂直分量为零，而两悬挂点处轴向张力的垂直分量都比较大。式(3)适用于等高架空线和不等高架空线，当两悬挂点等高时，这2个挂点处的轴向张力相等且最大;而两悬挂点不等高时，处于较高位置处的悬挂点的轴向张力最大。

将la和lb代入式(3)中，可得悬挂点A、B处的轴向张力分别为

2 导线找形的有限元法

2.1 架空线找形

架空线找形是为了确定架空线在仅承受自重或者预应力作用下的自平衡状态，不考虑荷载的作用，该状态提供了分析结构在外部荷载作用下所必须的所有初始条件，如结构几何形状和预应力等［5］。因此，架空线的初始位形是进行工作状态分析的前提，也是进行模态分析确定自然频率和振型等振动特性的基础［6］。

由式(2)可知，架空线的弧垂和水平张力互为结果，必须已知其中1个参数才能唯一确定架空线的线形或张力［7］。在工程设计时，可根据实际要求确定架空线的弧垂，或者根据应力条件预先给定架空线的张力，只有这样才能确定架空线的初始状态，由初始状态再进行后续的工作状态分析。

架空线找形方法有2种，即直接迭代法和找形分析法。

2.2 直接迭代法

直接迭代法基本原理是在导线曲弦线位置创建模型，采用实际材料性质和实常数，并设置很小的初应变，施加自重荷载(沿弧长分布)，逐步更新有限元模型，以导线水平张力为收敛条件进行迭代，其最终结果即为导线在自重荷载作用下的初始变形［8］。

(1)创建几何模型和有限元模型:在导线弦线位置上创建几何模型，如图1中的直线AB。设置实际的材料性质和实常数，设置任意很小的初应变以获得求解稳定性，因为张力是荷载作用而产生，所以导线不能采用较大的初应变。

(2)求解并不断更新有限元模型:施加自重荷载后求解。更新有限元模型不断改变导线的几何状态，如果求解后的结果不能满足收敛条件，则继续求解直到满足迭代要求的收敛条件。此过程结束后获得初始状态，即在自重荷载作用下导线的内力和几何状态。

(3)施加外荷载求解:在获得导线的初始状态后，就可以施加其他外荷载，进行工作状态分析。

2.3 找形分析法

找形分析法的基本原理是在架空线曲弦线位置创建模型，采用很大的初始应变和较小的弹性模量，施加自重荷载，其变形即为初始状态的线形。在此线形下恢复实际弹性模量，假定很小的初始应变，求得导线在自重荷载作用下的初始状态［9］。

(1)找形分析。找形分析时应设置较大的初应变，以便较快收敛。可根据初始水平张力和初应变，确定“假定较小的弹性模量”。创建几何模型并生成有限元模型，施加荷载和约束后求解。

(2)初始状态分析。找形分析后恢复真实的弹性模量，并设置很小的初应变以获得求解稳定性。该求解过程中如果导线的水平张力与已知的张力不符，可采用类似“直接迭代法”中的迭代过程。

(3)工作状态分析。在初始状态分析完成后即可施加外荷载进行分析，从而获得基于初始状态的外荷载作用下的结果。

2.4 实例计算

本文使用直接迭代法对算例进行找形，取某架空线为例，其基本参数如下:截面积为701.6 cm2，档距为120 m，弹性模量为78.9 GPa，单位长度自重力为65 N/m，水平张力为9 kN，两悬挂点高差为20 m。选用LINK10单元，根据两悬挂点的位置参数建立导线的初始模型，即为1条连接两悬挂点的线段。接着进行实参数设置和网格划分，施加载荷并添加边界条件，然后进行迭代找形计算。迭代部分的命令流如下:

其中:ENUM为网格划分数;H0为初始水平张力值;NODE1、NODE2为跨中单元的2个节点。

通过ANSYS迭代分析得到架空导线的初始位形，如图4所示。其中斜直线段为导线模型，弧线段所处位置为导线找形后的悬垂状态。

图4 导线找形后的悬垂状态Fig.4 Suspended state of form-finding conductor

架空导线部分参数的理论值与ANSYS结果见表1。由表中数据可以看出，跨中弧垂、索长和最大张力等参数的理论计算值与ANSYS软件的分析结果相差甚小，最大误差仅为0.89%，说明找形结果是正确的，验证了找形方法的可行性和可靠性。

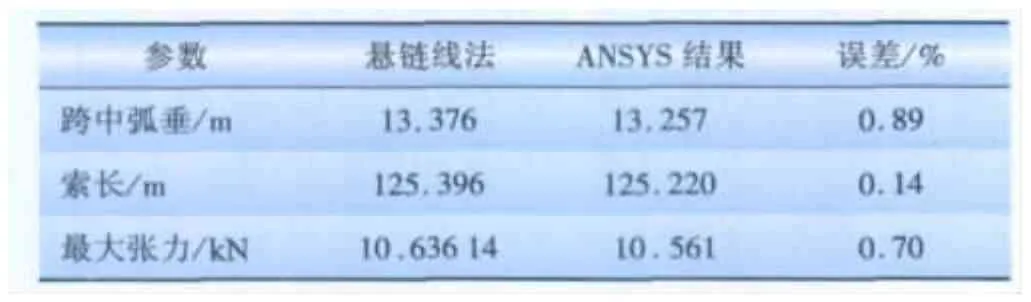
表1 架空线部分参数的理论值与ANSYS值Tab.1 Comparison of theoretical values with ANSYS results

3 结语

架空线找形是动力学分析的前提，找形的精度直接影响动力响应的结果［10］。本文介绍了架空线找形研究的解析法和有限元法，并针对索单元的几何非线性特点，介绍了用ANSYS进行非线性有限元找形的思想。通过算例计算，验证了ANSYS找形的可行性和正确性，为架空输电导线的工作状态分析提供了条件。

［1］孟遂民，孔伟.架空输电线路设计［M］.北京:中国电力出版社，2007.

［2］卫星，强士中.利用ANSYS实现斜拉桥非线性分析［J］.四川建筑科学研究，2003，29(4):41-43.

［3］李博之.高压架空输电线路架线施工计算原理［M］.北京:中国电力出版社，2008.

［4］王月.索膜结构找形分析的有限元法及ANSYS实现［J］.辽宁工程技术大学学报，2005，24(4):104-107.

［5］Agamenon R E O，Denise G F.Dynamical modeling and analysis of Aeolian vibrations of single conductor［J］.IEEE Trans on Power Delivery，1994，9(3):1685-1693.

［6］Papailiou K O.On the bending stiffness of transmission line conductors［J］.IEEE Trans on Power Delivery，1997，12(4):1 576-1 588.

［7］Rawlins C B.Research on vibration of overhead ground wires［J］.IEEE Trans on Pow er Delivery，1988，3(2):769-775.

［8］夏正春，李黎，梁政平，等.输电塔在线路断线作用下的动力响应［J］.振动与冲击，2007，26(11):45-49.

［9］孟遂民，单鲁平.输电线动力学分析中的找形研究［J］.电网与清洁能源，2009，25(10):43-47.

［10］王少华.输电线路覆冰导线舞动及其对塔线体系力学特性影响的研究［D］.重庆:重庆大学，2008.