变电站主变压器档位设置预优化方法
2012-08-09郑海坤刘瀚林
郑海坤,刘瀚林
(1.广东电网公司梅州供电局,广东省梅州市,528400;2.华南理工大学电力学院,广州市,510640)
0 引言
对电网实施无功优化调度主要有以下几个手段:调节发电机机端电压、调整变压器抽头档位以及投切无功补偿设备。通过几种手段的配合,能达到满足电网无功电压的需求,优化潮流分布,减小网损的目的[1-4];同时可尽量减少设备动作过于频繁,以增加设备的可靠性和使用寿命[5-7]。
当前对无功优化的研究十分广泛,相关的软件和算法等也在不断改进[8-12]。自动电压控制系统(automatic voltage control,AVC)在调度运行中的应用也日益普及,是一种综合各种调控手段的全网优化控制[13-14]。但是随着电网规模的扩大,控制变量特别是连续变量的增多,造成了求解机时大大增加,而优化质量也明显下降。尽管无功优化的手段是不可分割的,但如果将几种手段解耦分别进行研究,可得到相近解,并大大简化求解时间。
本文针对变压器抽头的档位调节进行研究,提出变压器调节效应指标,定量衡量变压器抽头档位变化引起的电网电压及无功变化,分析得知各变压器的调节近似独立,调节效果能够相叠加,并在改变无功潮流最小的前提下,通过不同的叠加组合寻求满足调压需求的最优解。
由于变压器抽头档位属于离散变量且取值范围较小,即使对于大规模电网,也能快速得到优化解,故该方法可在负荷预测基础上进行变电站档位设置规划。另外,无论启发式算法还是基于数学模型的全局寻优算法,均将电网初始状态作为原点开始寻优。因此,本方法亦可作为一种在线辅助决策,即全局优化前的预优化计算,将预优化结果作为初值进行全局寻优,使初始状态更接近最优解,从而减小总体寻优时间。
1 一档调节效应指标
本文提出一档调节效应指标,分别是一档电压效应(voltage effect per tap,VPT)及一档无功效应(reactive effect per tap,QPT),用以表征系统各节点电压以及系统各元件注入无功因变压器调整一档带来的变化量。
在电网正常运行时不可能对变压器抽头档位做大幅的改变,因此可认为每级的调节效应基本一致;由于上、下调档具有对称性,本文以上调档位计算调节效应,而下调则取其相反数,另外,变电站所有变压器均认可为一致调档。
1.1 一档电压效应
一档电压效应指标表征变压器抽头调节一档所引起电网各节点电压的变化情况,定义式为

式中:ΔVij为第i台变压器对第j个节点的一档电压效应;Vj0、Vj分别为i变压器档位上调前后节点j的电压标幺值。
一档电压效应指标体现了变压器调档导致节点电压改变的步长,本质上反映了电网中各节点电压对该变压器调档的灵敏度。
1.2 一档无功效应
一档无功效应指标表征变压器调整一档带来的系统各元件注入无功的相对变化,定义式为

式中:ΔQij为第i台变压器对第j个节点的一档无功效应;Qj0、Qj分别为i变压器档位上调前后节点注入无功标幺值(以100 Mvar为基准)。
无功效应指标能反映由变压器调档导致的无功变化情况,采用一档调节无功效应指标反映因变压器调档引起的节点无功变化,作为是否允许调档、调档幅度、需要如何配合的依据。
1.3 调节效应的相对独立性和可叠加性
假定一个简单系统,由系统通过线路连接2台变压器供应负荷,由于高压系统中的R<<X,故忽略电阻的影响,如图1所示。
图1 中,Vs为系统电压,X1、X2为线路电抗,X1T、X2T为变压器等值电抗,P1+j Q1、P2+j Q2分别为2台变压器所带负荷。变压器高压侧无功等于无功负荷QL与变压器无功损耗QT之和,即

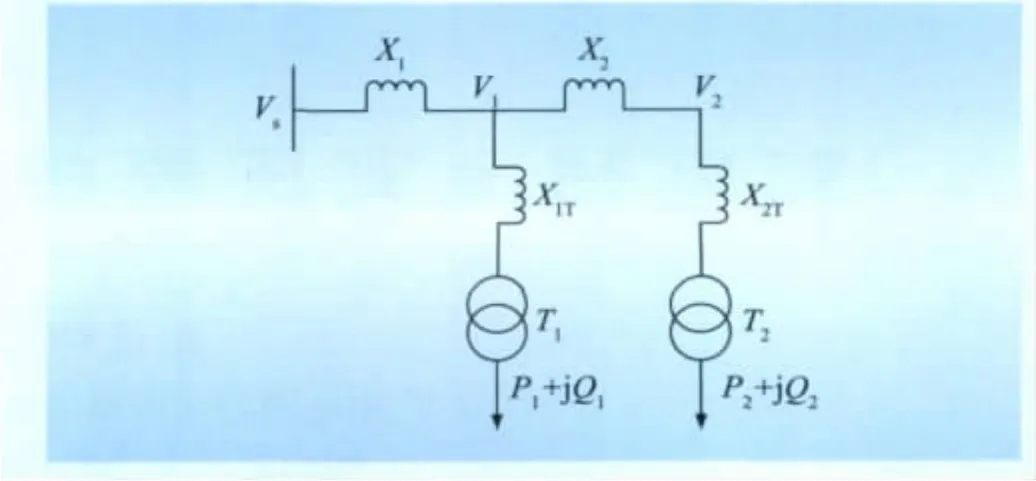
图1 简化系统接线图Fig.1 Simplified wiring diagram of system
高压侧电压V1、V2分别根据下式计算:

式中:∑Q1、∑Q2分别为变压器 T1、T2的高压侧无功;Qloss1、Qloss2为线路的无功损耗。
由电网运行经验可知,220 kV变压器抽头变动1档导致高压侧无功功率变化不大于1 Mvar(AVC设置的最大变化一般为0.3~0.5 Mvar),远小于无功负荷与变压器无功损耗之和,即ΔQ <<∑Q,将ΔQ加至式(4)中分子的括号中即可计算调档后的V1、V2。
任意1台变压器进行一档调节,对自身的中低压侧无功电压改变较明显,而线路上流动的无功量改变都不大,线路两端压降基本不变,故变压器高压侧电压及其他未动作的变压器的无功功率也只会有轻微影响。而对于上层500 kV变压器调档,即相当于图1中Vs改变,对220 kV层面的电压无功变化的影响是等同的。
由于是在当前运行点附近作调整,某一变压器动作引起的相对变化量基本不因其他同等级变压器动作而改变;又因上层对下层电网的电压无功影响是均匀的,可认为所有变压器的调档动作效果等于全部调节效应之和,即调节效应具有相对独立性和可叠加性。
2 调控策略的数学模型
由于110 kV变电站之间的电气距离较近,且部分地区存在环网情况,相邻2站间的调档相互影响较大,不具备叠加性质,故本文只讨论220 kV及以上主网的调节问题。
2.1 变量及指标说明
设某简单电网系统具有l条母线,m台500 kV有载调压变压器,n台220 kV有载调压变压器,对于全网中所有的500、220、110、35、10 kV 母线进行排序编号形成序列(1,2,…,l),在当前潮流下计算调节效应,第i台500 kV有载变压器对所有母线的一档电压效应列向量为
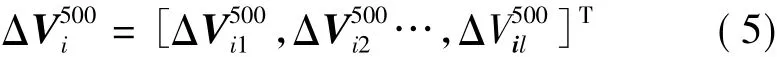
式中:i=1,2,…,m。
第j台220 kV有载变压器对所有母线的一档电压效应列向量为
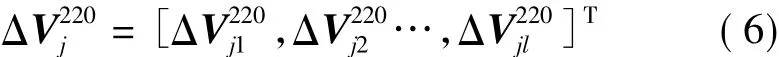
式中:i=1,2,…,n。
第i台500 kV有载变压器对所有母线的一档无功效应列向量为

式中:i=1,2,…,m。
第j台220 kV有载变压器对所有母线的一档无功效应列向量为
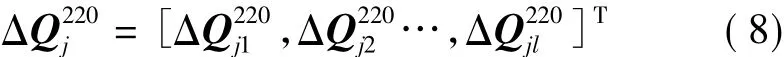
式中:i=1,2,…,n。
所有母线的初始电压值为

优化后电压应在该上下限的目标范围内,即
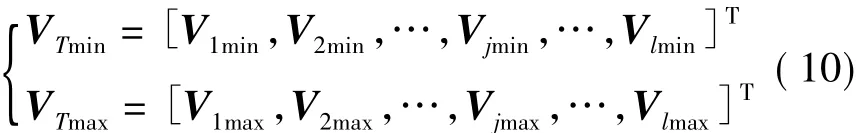
式中:VTmin和VTmax分别是母线电压的上下限列向量。
500 kV和220 kV变压器的动作档数列向量分别表示为
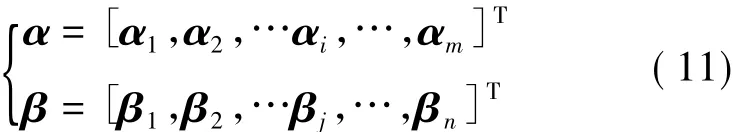
式中:αmin,αmax,βmin,βmax分别表示变压器抽头动作的上下限,由变压器自身限制或上级调度部门给出;正数代表上调档位,负数代表下调档位。
2.2 目标函数
对于地区电网(特别是无功平衡情况较差的电网),为避免出现满足某侧电压要求的同时导致其他侧电压恶化的情况,应该尽量减小调档引起的注入无功改变量。本文的控制策略以上述2个主要因素作为优化对象,即基于动作次数和无功变化量最小进行优化,目标函数为

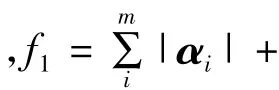
2.3 约束条件
由于本文提出的策略的数学模型只考虑变压器调档因素,故约束条件较常规无功优化略有简化,即控制后的全网节点电压需在目标范围内,且变压器抽头动作不得超过允许值:

式中:ΔV为全网节点电压的变化列向量,由所有变压器电压效应及对应动作的乘积之和,为

3 实际算例
3.1 项目背景
以某电压长期偏高的实际电网作为算例。该地区位于华南,水系发达,拥有大量小水电站接入电网。另外,由于当地经济欠发达,因此负荷水平相对较低。这种较为特殊的网架结构和负荷电源特性导致该地区电压长期偏高,且难以满足无功分层分区就地平衡的需要,不但不利于经济运行,也威胁着运行安全性。
该地区的220 kV及以上的主网架中包括43个母线节点,4座发电厂,1座500 kV变电站1台主变,8座220 kV变电站14台主变,所有变压器均为有载调压变压器。
在夏小方式下,该地区电网水电充足,而负荷相对较轻,易出现电压偏高乃至越上限问题。因此本算例将在夏小方式下进行调档分析计算。
3.2 发电厂的处理方法
由于存在若干220 kV上网的发电厂,而电厂一般按照PV或PQ节点处理,取PV节点居多。现分别对2种情况进行计算,分析何种方法适用于本文模型,以该地区的500 kV变压器为例,进行变化。表1为计算结果。
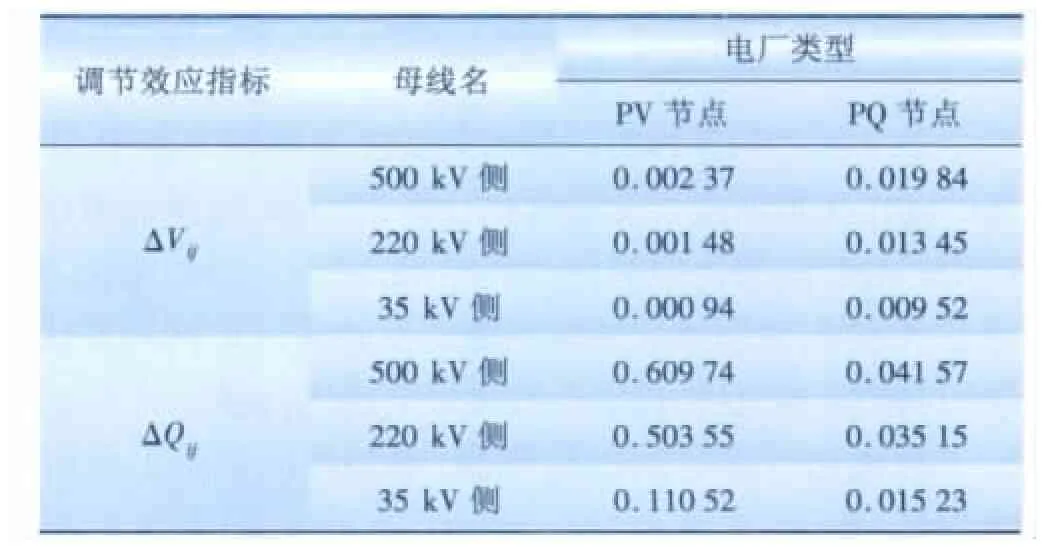
表1 500 kV主变一档调节效应指标Tab.1 Adjusting effect of 500 kV transformer
由表1可看出电厂作为PV节点时,电压效应极小,而无功效应却很大,相反,当电厂作为PQ节点时,变压器调档对节点电压和无功的调控较为均衡。更为重要的是,本文模型是基于调节效应可叠加的前提,PV节点使得220 kV层的电压被钳定,导致电压效应难以满足叠加条件,且定电压调档将引起发电机的无功出力剧烈变化,不符合实际运行情况。因此,调节效应也将发电厂作为PQ节点进行计算。
3.3 计算一档调节效应
由于全网共9个变电站43个节点,限于篇幅,电压效应和无功效应列向量不在此列出。
从调节效应列向量的计算值可看出,对于500 kV变压器,其调节具有均匀的全网影响性,对全网节点电压效应均约为0.015,无功效应基本仅对其自身影响较明显;对于220 kV变压器,其无功和电压调节效应在自身节点较为明显,而对其他节点电压和无功基本无影响,也验证了上文所述调节独立性假设,并且使得电压效应和无功效应列向量中有大量的零元素,显著简化向量的运算处理。
3.4 变压器档位优化计算及分析
现采用本文提出的方法进行变压器档位优化计算,再与直接利用软件进行无功优化(包括发电机、变压器、无功补偿的调整)的结果相对比。得到2种方法计算的变电站调档结果,如表2所示。
表2所列的2种方法得出的变电站调档方案中,本文的动作次数略多于无功优化计算的结果,这是仅考虑调档的必然结果。但对比优化结果,发现2者的调整方向是一致的,说明本文的策略能够反映实际电网对变压器的调档需求,且档位动作数接近全局优化解。
对优化计算时间进行考察,本文调档策略生成时间为0.064 s,全局优化时间为2.571 s,前者远小于后者;另外,若把前者的结果作为初值再进行全局优化,则计算时间为1.856 s,总和1.92 s,小于直接采用全局优化的时间,因此本文的方法作为预优化能使计算时间进一步减少。
4 结语
本文提出一种简单实用变压器档位设置策略,实现快速的变压器档位优化。无功优化主要手段是无功补偿,辅助分接头操作,因此本文策略可用于变电站档位设置规划;在实时调度中并非直接执行,而是给定更好的全网优预化初值,利于AVC系统更快求解全网优化。最后通过算例对比,验证了本方法作为一种快速优化或预优化方法的有效性和可行性。
[1]张勇军,任震,李邦峰.电力系统无功优化调度研究综述[J].电网技术,2005,29(2):50-54.
[2]Cova B,Losignore N,Marannino P.Contingency constrained optimal reactive pow er flow procedures for voltage control in planning and operation[J].IEEE Trans on Power Systems,1995,10(2):602-608.
[3]董洁,赵凤展,杨仁刚.采用启发式策略的动态无功优化混合算法研究[J].电力系统保护与控制,2011,39(5):35-40.
[4]张勇军,俞悦,任震,等.实时环境下动态无功优化建模研究.电网技术,2004,28(12):12-15.
[5]颜伟,田甜,张海兵,等.考虑相邻时段投切次数约束的动态无功优化启发式策略[J].电力系统自动化,2008,32(10):71-75.
[6]杨素琴,韩念杭.计及调节次数的变电站动态电压无功优化控制的研究[J].电力系统保护与控制,2010,38(24):131-136.
[7]刘明波,朱春明,钱康龄,等.计及控制设备动作次数约束的动态无功优化算法[J].中国电机工程学报,2004,24(3):34-40.
[8]张安安,洪耕.基于ε-支配域的模糊多目标无功优化方法[J].电力系统自动化,2009,33(5):34-38.
[9]钟红梅,任震,张勇军等.实时无功优化软件ORP的开发与应用[J].继电器,2004,32(11):55-57..
[10]刘志文,刘明波.基于Ward等值的多区域无功优化分解协调算法[J]. 电力系统自动化,2010,34(14):63-68.
[11]刘丽军,李捷,蔡金锭.基于强引导粒子群与混沌优化的电力系统无功优化[J].电力自动化设备,2010,30(4):71-75.
[12]刘伟,梁新兰,安晓龙.基于蜜蜂进化型粒子群算法的电力系统无功优化[J].电力系统保护与控制,2010,38(7):16-21.
[13]钟毅,陈蕊.地区电网AVC系统设计与实现[J].电力系统保护与控制,2008,36(23):41-44,53.
[14]李钦,温柏坚.广东电网电厂AVC子站建设研究[J].电力系统保护与控制,2008,36(21):38-42.
