可再生能源发电优化模型及其应用

从荣刚

(1.华北电力大学经济与管理学院，北京市 102206;2.瑞典隆德大学环境与气候研究中心，瑞典隆德市 22362)

0 引言

我国政府承诺到2020年中国可再生能源消费要占一次能源消费的15%，使可再生能源的发展在我国受到了空前的关注。一方面，开发可再生能源对于保障能源的供给安全意义重大［1］;另一方面，20世纪80年代以后，随着全球气候变暖和大气环境质量的急剧下降，人们对环境保护和可持续发展问题达成共识。

可再生能源发电是可再生能源的主要利用领域之一。影响可再生能源发电的主要因素有:技术开发利用成本、资源潜力、技术成熟度、经济发展和环境约束等［2-3］。对可再生能源发电的最大利用规模和结构进行科学的分析，有助于国家相关部门和电网公司提早开展规划，减少过剩投资和不足投资的可能性，为可再生能源的发展提供输送保障，因此具有深刻的现实背景和很高的应用价值。

20世纪80年代，国外对可再生能源的综合利用进行了研究。文献［4］指出，从能源生产和利用的角度来看，基于太阳能、风能和生物质能的可再生能源集成利用系统(integrated renewable energy system，IRES)的概念是可行的。文献［5］利用线性规划方法开发了IRES模型，其目标是在能源和电力的资源约束下，最小化每年的成本。文献［6］立足于技术经济的观点设计IRES模型，并且把电力供给的损失作为重要的系统变量。文献［7］开发了最优可再生能源模型(optimization renewable energy model，OREM)，在社会接受度、资源、需求和可靠性条件等约束下最小化成本与效率的比值，共考虑了约38种不同的可再生能源选项。文献［8］利用修正的计量数学模型，基于能源-环境-经济的数学规划模型和OREM模型研究了印度可再生能源的最优利用问题，充分考虑了成本、效率、社会接受度、可靠性、潜力和环境等因素的影响。

本文采用数学优化思想对可再生能源发电进行综合规划，所提出的模型充分考虑了可再生能源技术的学习效应及其技术成熟度等因素对可再生能源发电规模化发展的影响，并将模型实现动态化，以实现对可再生能源发电在一段时期内的发展路径进行优化。

1 可再生能源发电成本变化规律

1.1 考虑最低单位投资成本的学习曲线模型

可再生能源的发电成本是影响可再生能源发电规模化发展的重要因素之一。从国内外的经验来看，学习曲线模型被广泛用来描述和预测可再生能源发电成本下降的规律，其核心思想是当可再生能源发电的累积装机容量每增加1倍，其单位建设成本就出现一定比例的下降［1-15］。本文考虑了最低单位投资成本(即风电机组投资成本的下降必然存在一个下限)，尝试通过分析中国主要的3种可再生能源发电(风电、太阳能光伏发电和生物质发电)的累积装机容量与单位投资成本的关系，来揭示其投资成本的变化趋势。

可再生能源的单位投资成本与累积装机容量之间的关系为

式中:C(t)为单位机组投资成本;Cmin为单位机组投资成本下限;C0为初始时刻的单位机组投资成本;N(t)为机组的累积装机容量;φ为累积产量对单位投资成本的弹性系数;μ(t)为随机干扰因素。

为了方便计算，对(1)式进行变换，得到

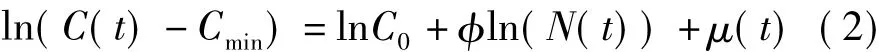
这样，利用最小二乘法就可以估算出累积装机容量对单位投资成本的弹性系数。

1.2 3种可再生能源发电的学习曲线效应

根据学习曲线模型，得到我国风电和太阳能光伏发电单位投资成本的学习效应，结果如表1、2所示。

表1 风电的学习曲线效应Tab.1 Learning curve effect of wind power

表2 光伏发电的学习曲线效应Tab.2 Learning curve effect of photovoltaic power generation

目前，各类生物质发电尚未进入规模化发展阶段，相关数据缺乏。根据文献［13］的研究结果，生物质发电的学习曲线设定为

式中:Cb(t)为生物质发电单位机组投资成本;Nb(t)为机组的累积装机容量。

2 可再生能源发电技术成熟度

2.1 可再生能源技术成熟度模型

可再生能源的规模化发展离不开相关的技术支撑。技术系统的进化要经历婴儿期、成长期、成熟期和衰退期4个阶段，这些阶段组成了其技术生命周期，通常用S曲线表示［14］。一方面，在可再生能源建设初期，受需求、电网建设等约束，可再生能源发展呈现缓慢发展趋势;另一方面，在可再生能源建设的中后期，随着相关配套设施和市场的逐渐成熟，可再生能源发展将呈现快速发展直至饱和的特点。实际上，可再生能源发展的规模应该小于或等于S型曲线的预测结果，即S型曲线预测的应为累积装机容量的上限(潜力)。本文采用S型曲线对可再生能源发电的技术成熟度进行建模，技术扩散模型为

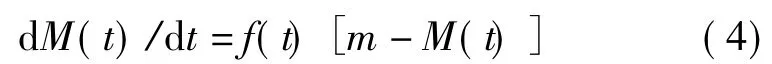
式中:M(t)为t时刻可能的最大装机容量;m为理论上的最大装机容量;f(t)为时间依赖函数，其表达式为

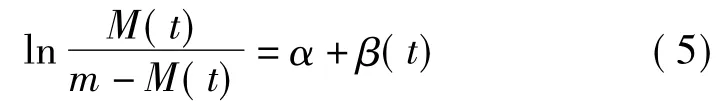
式中:α 和 β 是待估参数［15］。

2.2 3种可再生发电的技术成熟度效应

通过对中国风电累计装机容量的拟合，得到风电累积装机容量的S型曲线模型的参数，结果如表3所示。根据模型估算，2015年中国风电累计装机容量潜力可达到92 GW，2020年可达到233 GW。

表3 风电累积装机容量的S型曲线模型拟合参数Tab.3 Fitting parameters of S-curve model for wind power’s cumulative installed capacity

采用同样的方法对光伏发电进行计算，得到光伏发电累积装机容量的S型曲线模型的参数，结果如表4所示。根据模型估算得出，2015年中国光伏发电累计装机容量潜力可达到800 MW，2020年可达到2 668 MW。这里预测的结果和07年发布的《可再生能源中长期发展规划》类似，由于最新的《新能源发展规划》草案将原来的规划值提高了10多倍，在后面的模型分析中，将对应的预测值扩大10倍处理。

表4 光伏发电累积装机容量的S型曲线模型拟合参数Tab.4 Fitting parameters of S-curve model for photovoltaic power’s cumulative installed capacity

由于我国生物质发电起步较晚，尚缺乏一定量的历史数据，生物质发电的技术成熟度效应主要是根据相关的生物质发电厂建设规划来进行判断。2010年生物质发电装机容量潜力可达到5 500 MW，2020年可达到30 000 MW。

3 中国可再生能源发电优化模型

根据技术扩散和经济约束等条件，预测2015、2020年我国可再生能源发电(风电、光伏发电和生物质发电)的总体利用规模及结构。借鉴 IRES和OREM可再生能源综合利用模型的思想，选用运筹学中的动态优化模型来计算。目标函数是最大化3种可再生发电的总发电量，风电、光伏发电和生物质发电的年平均可利用时间分别为2 000、1 300、2 380 h，约束条件包括:(1)各种可再生能源发电的装机容量小于其各个时间点的最大容量值(由技术成熟度模型给出);(2)各种可再生能源发电装机的投资在经济可承受的范围内;(3)可再生能源发电的上网规模小于一定的比例(并网限制);(4)各种可再生能源发电满足国家规划。控制变量为2011—2020年3种可再生能源发电的新增装机容量，一方面其需要在各个时间点满足各方面的约束;另一方面，各个时间点的装机容量会对以后的单位成本产生影响(学习效应)。具体的优化模型为

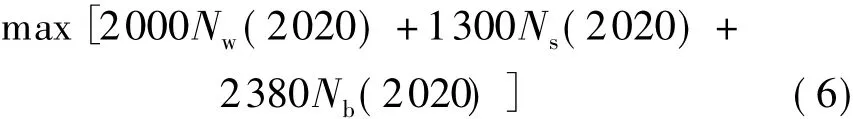
式中:Nw为风电的装机容量;Ns为光伏发电的装机容量;Nb为生物质发电的装机容量。模型的约束条件为

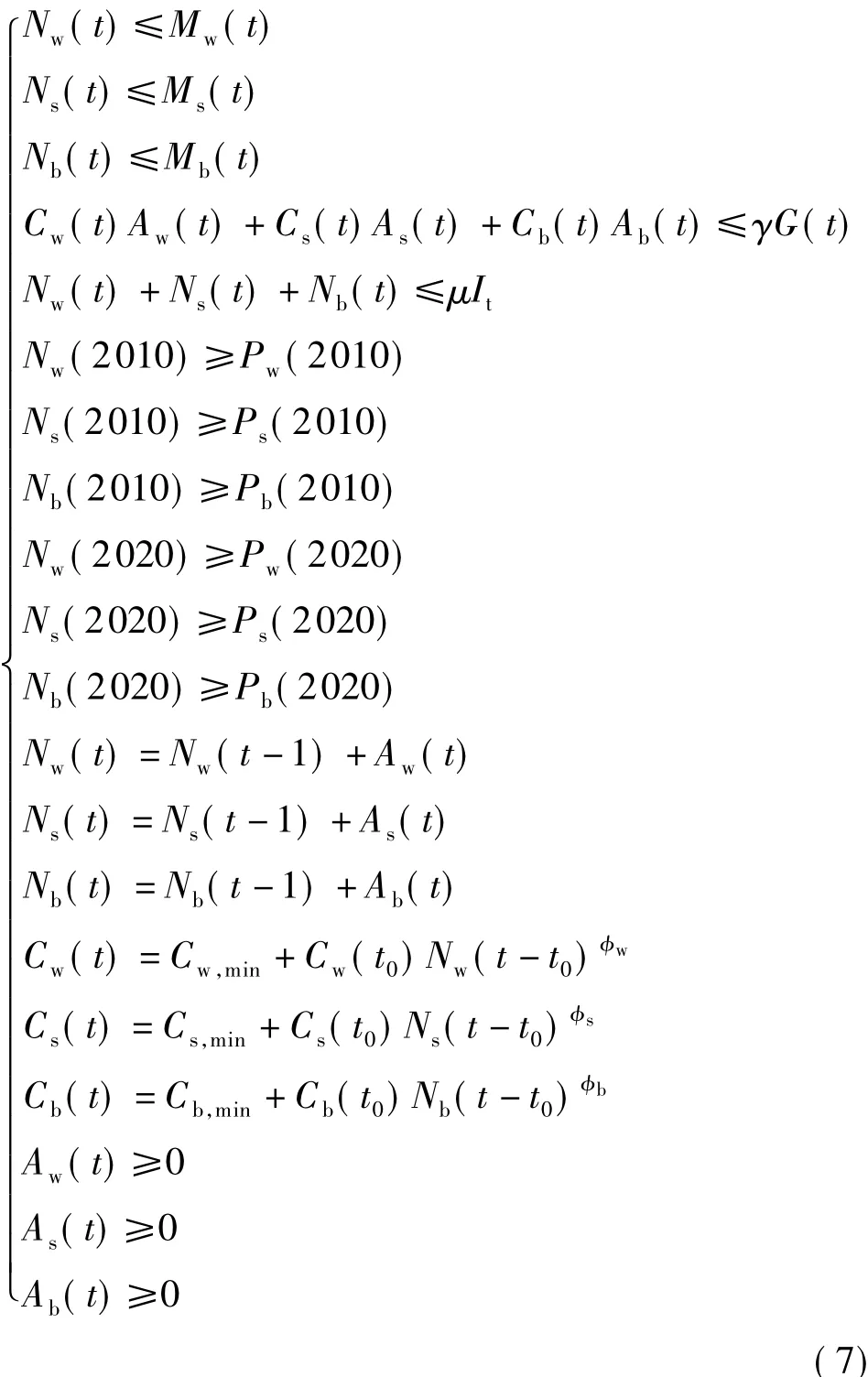
式中:Mw为风电的最大装机容量;Ms为光伏发电的最大装机容量;Mb为生物质发电的最大装机容量;Cw为风电的单位装机成本;Cs为光伏发电的单位装机成本;Cb为生物质发电的单位装机成本;Aw为风电的年新增装机容量;As为光伏发电的年新增装机容量;Ab为生物质发电的年新增装机容量;γ为GDP中用于可再生发电方面的投资比例;G(t)为第t年的GDP总量;μ为可再生能源发电最大上网比例;It为t时刻的总装机量;Pw为风电的装机规划量;Ps为光伏发电的装机规划量;Pb为生物质发电的装机规划量;Cw，min为风电的最小装机价格;Cs，min为光伏发电的最小装机价格;Cb，min为生物质发电的最小装机价格。

4 模型计算结果和敏感性分析

4.1 模型计算结果

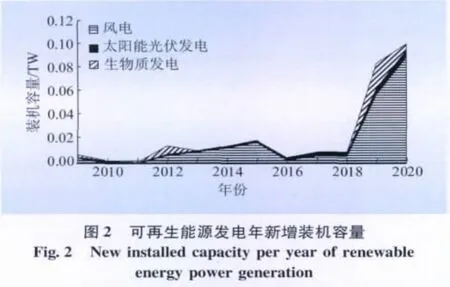
利用本文提出的模型，分别计算了3中可再生能源发电在最大利用情景下的累计装机容量、年新增装机容量、单位投资成本，结果如图1—3所示。

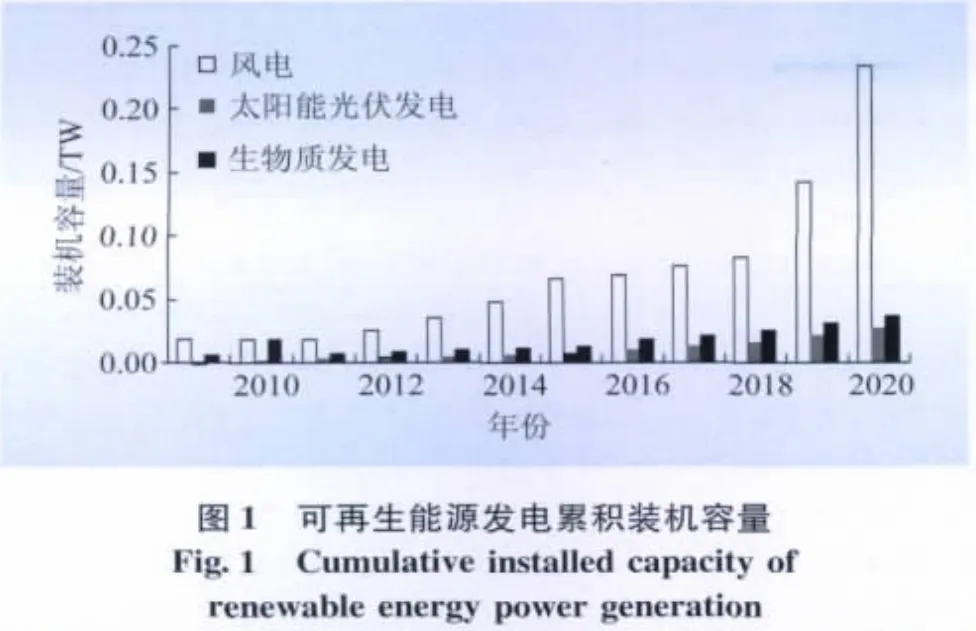
从图1可看出:在最大利用情景下，2015年风电、太阳能光伏发电和生物质发电的累积装机容量分别为65 999、8 000、12 210 MW，2020 年三者的累积装机容量分别为233 321、26 680、35 506 MW。根据《新能源振兴规划》草案和《可再生能源中长期发展规划》，2020年风电、太阳能光伏发电、生物质发电的预期装机容量将达到150 000、20 000、30 000 MW。计算得到的最大利用情景下，3种可再生能源的总规模比规划情景高出47.75%，风电、太阳能光伏发电和生物质发电的实际最大利用规模分别比规划情景高出55.5%、33.4%、18.4%。可以看出，与生物质发电相比，风电和太阳能光伏发电还具有相当大的发展潜力。

从图2可看出:生物质发电在初期得到了较快的发展，2009年增装机容量达到了2 659 MW;而风电则主要是在2012年后得到了较快的发展，2012—2020年的平均年新增装机容量达到了22 198 MW，并且呈现总体上涨的趋势;太阳能光伏发电则保持相对平稳的增长态势，平均年新增装机容量达到了2 211 MW。

从图3可看出，3种可再生能源发电的单位投资成本均呈现随时间下降的趋势。其中:由于太阳能发电在2010年的新增投资较大，使其单位成本出现较大的下降，从而为其后的规模化发展创造条件;2015年风电、太阳能发电和生物质发电的单位投资成本分别为0.49、1.33、0.58万元/kW，2020年的单位投资分别为0.44、1.1、0.57万元/kW。

4.2 主要不确定因素的敏感性分析

可再生能源发电最大规模的确定，受电网技术、宏观投资比例等多方面因素的影响，而这些因素本身存在着较大的不确定性。因此，为了科学分析可再生能源发电的最大规模，对主要的不确定性因素进行了敏感性分析，结果如图4、5所示。

图4 投资比例对2020年3种可再生能源最大发电规模的影响Fig.4 Impact of investment proportion on scales of renewable energy power generation in 2020

由图4可看出:当γ从2‰上升到5‰时，可再生能源发电最大规模接近饱和;当γ小于1‰时，模型无法得到可行解。随着投资比例的增加，风电得到了较大的发展，γ=2‰时，2020年风电累积装机容量为139 049 MW;γ=4‰时，风电的累积装机容量为23 321 MW，增长了67.7%;相比之下，太阳能光伏发电和生物质发电仅增长了33.4%和18.35%。

由图5可看出:随着μ的增加，可再生能源的最大发电规模趋向饱和;μ增大主要对风电和太阳能发电的2020年的累积装机容量产生影响;μ=0.15时，风电和太阳能发电2020年的累积装机容量分别为163 494、20 000 MW;μ≥0.25时，风电和太阳能发电2020年的累积装机容量分别为233 321、26 680 MW。

5 结论

(1)2015年风电、太阳能光伏发电和生物质发电的累积装机容量分别为65 999、8 000、12 210 MW，2020年三者的累积装机容量分别为233 321、26 680、35 506 MW。

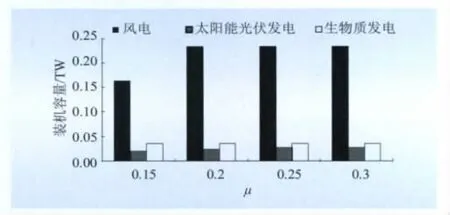
图5 可再生能源上网比例对2020年3种可再生能源最大发电规模的影响Fig.5 Impact of grid connected proportion on scales of renewable energy power generation in 2020

(2)考虑到了发电成本的下降以及发电技术扩散效应的约束，3种可再生能源发电的年新增装机容量呈现出了不同的特点。生物质发电在初期得到了较快的发展，而风电则主要是在2012年后得到了较快的发展，并且呈现总体上涨的趋势，太阳能光伏发电则保持相对平稳的增长态势。

(3)随着可再生能源装机容量的扩大，其对应的单位投资成本也呈现出下降的趋势。其中，太阳能发电在初期的新增投资较大，使其单位成本出现较大的下降，从而可以为其后的规模化发展创造条件。2015年风电、太阳能发电和生物质发电的单位投资成本分别为0.49、1.33、0.58万元/kW;2020年的单位投资分别为0.44、1.1、0.57万元/kW。

(4)经济约束主要对风电产生较大的影响，而对太阳能光伏发电和生物质发电影响较小。而可再生能源上网比例的增加，主要对风电和太阳能发电的2020年的累积装机容量产生影响。

［1］盛明科，甘纪平.论低碳经济发展背景下我国能源政策的失灵与矫正［J］. 吉首大学学报:社会科学版，2010，31(6):79-83.

［2］李虹，董亮，段红霞.中国可再生能源发展综合评价与结构优化研究［J］. 资源科学，2011，33(3):431-440.

［3］陶建格，薛惠锋，能源约束与中国可再生能源开发利用对策［J］.资源科学，2008，30(2):199-205.

［4］Jain B C.Rural energy centres based on renewable-case study on an effective and viable alternative［J］. IEEE Trans on Energy Conversation，1987，2(3):329-335.

［5］Ramakumar R，Shetty P S，Ashenayi K.A linear programming approach to the design of integrated renewable energy systems for developing countries［J］.IEEE Trans on Energy Conversion，1986，1(4):18-24.

［6］Ashenayi K，Ramakumar R.IRES—a program to design integrated renewable energy system［J］.Energy，1990，15(12):1143-1152.

［7］Iniyan S，Jagadeesam T R.On the development of a reliability based optimal renewable energy model for the sustainable energy scene in India［J］.International Journal of Ambient Energy，1997，18(3):153-164.

［8］Iniyan S，Suganthi L，Samuel A A.Energy models for commercial energy prediction and substitution of renewable energy sources［J］.Energy Policy，2006，34(17):2640-2653.

［9］Argote L，Epple D.Learning curves in manufacturing［J］.Science，1990，247:920-924.

［10］Neij L.Use of experience curves to analyse the prospects for diffusion and adoption of renewable energy technology［J］.Energy Policy，1997，25(13):1099-1107.

［11］Neij L.Cost dynamics of wind power［J］.Energy，1999，24(5):375-389.

［12］Kuemmel B.Windpower econometrics［J］.Energy policy，1999，27(15):941-942.

［13］蒲晓璞，樊京春，王永刚.生物质能发电技术学习曲线和发电政策相互影响分析［J］.可再生能源，2009，27(3):84-88.

［14］叶金国，陈燕.我国能源产业系统的演化过程与混沌［J］.数学的实践与认识，2005，35(8):5-10.

［15］Collantes G O.Incorporating stakeholders'perspectives into models of new technology diffusion:The case of fuel-cell vehicles［J］.Technological Forecasting and Social Change，2007，74(3):267-280.