空间解析几何二次曲面伸缩法的MATLAB设计和实现
2012-08-08崔秋珍
崔秋珍
(洛阳理工学院,河南 洛阳 471023)
1.引言
空间解析几何是大学数学的主要课程。二次曲面是空间解析几何的主要内容之一,是学习多元微积分的几何基础,它具有很强的逻辑性、空间性和运动性。讨论二次曲面的图像的形成和性质通常有截痕法和伸缩法。然而,由于空间解析几何常规教材无法直观和动态地表现二次曲面的形成过程和图形之间的关系,从而给学生学习空间解析几何课程带来理解困难。而MATLAB作为具有强大功能的数学软件,被越来越多地应用于传统教学中。文献[1]讨论了利用MATLAB实现空间解析几何二次曲面截痕法的动画演示。本文探讨空间解析几何二次曲面伸缩法的MATLAB设计和实现。
2.二次曲面及其伸缩变形法
二次曲面:三元二次方程所表示的曲面称为二次曲面。
伸缩变形法:设S是一个曲面,其方程为F(x,y,z)=0,设S'为将曲面沿某个坐标轴伸缩λ倍所得的曲面,其方程为F'(x,y,z)=0。通过比较S和S'的图形变化和方程 F(x,y,z)=0及F'(x,y,z)=0的关系讨论二次曲面的形成和关系的方法称为伸缩法。
设将S的y、z坐标不变,x坐标沿x轴伸缩λ倍。显然,若(x,y,z)∈S,则(λx,y,z)∈S'。若(x,y,z)∈S',则(x,y,z)∈S。因此,对于任意的(x,y,z)∈S',有 F(x,y,z)=0,即 F(x,y,z)=0 为 S'的方程。同理,F(xy,z)=0 和 F(x,yz)=0分别为将S沿y轴或者z轴伸缩λ倍的曲面的方程。
例如,把圆锥面a2z2=x2+y2沿y轴方向伸缩倍,所得曲面方程为,此为椭圆锥面。
3.二次曲面伸缩法的MATLAB设计和实现
二次曲面生成常用MALTAB命令和功能:
mesh:生成由 x、y、z指定的网线面
surf:生成由x、y、z指定的带阴影的网面图
cylinder:生成一单位圆柱体的 x、y、z值
sphere:生成三维直角坐标系中的单位球体
程序设计思想:首先生成球面S:x2+y2+z2=1,然后将S沿 x、y、z轴方向伸缩 a、b、c倍。得到椭球面=1。
程序如下:
[x,y,z]=sphere;%建立单位球面网络
mesh(x,y,z);%生成单位球面网线图
surf(a*x,b*y,c*z);%沿 x、y、z 轴方向伸缩 a、b、c 倍的网面图
xlabel('x');ylabel('y');zlabel('z');%添加坐标轴标注
title('x^2/a^2+y^2/b^2+z^2/c^2=1')%添加标题
图1为单位球面网线图,图2为将单位球面沿x、y、z轴方向伸缩4、5、2倍后生成的椭球面。

图1 单位球面网线图
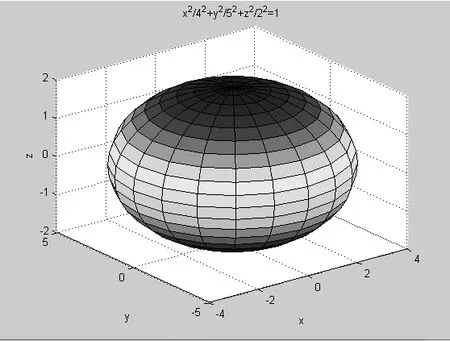
图2 椭球面
程序设计思路:首先生成曲面S:x2+y2=1+z2,然后将S沿 x、y、z轴方向伸缩 a、b、c倍。得到单叶双曲面 S’
程序如下:
z=linspace(0,1,40);%建立网络坐标

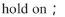
xlabel('x');ylabel('y');zlabel('z');%添加坐标轴标注
title('x^2/a^2+y^2/b^2-z^2/c^2=1')%添加标题
图3、图4给出a=2、b=4、c=5单叶双曲面的生成过程效果图。
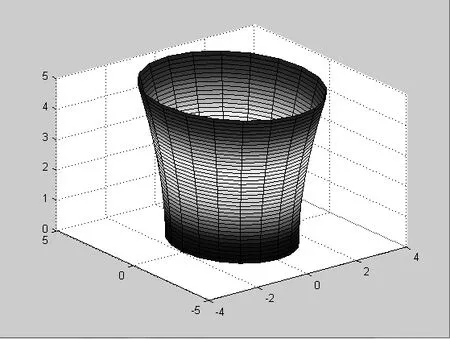
图3 单叶双曲面(z>0)
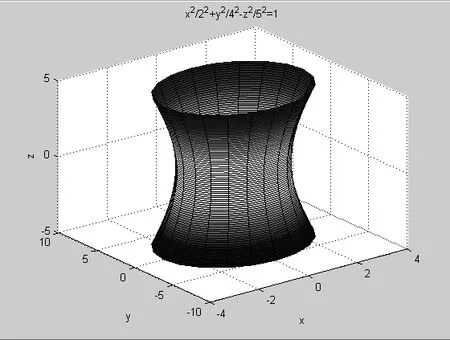
图4 单叶双曲面
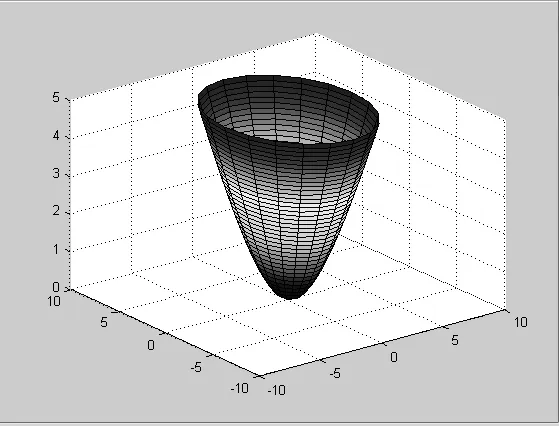
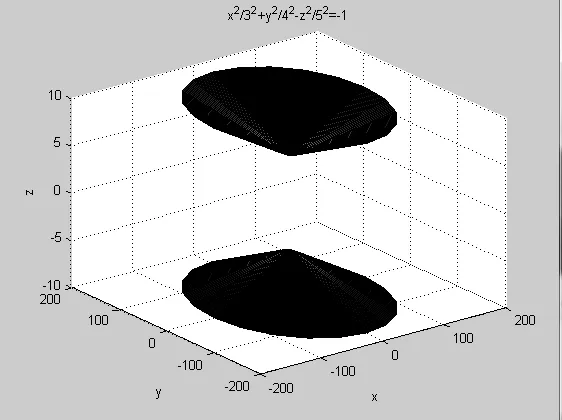
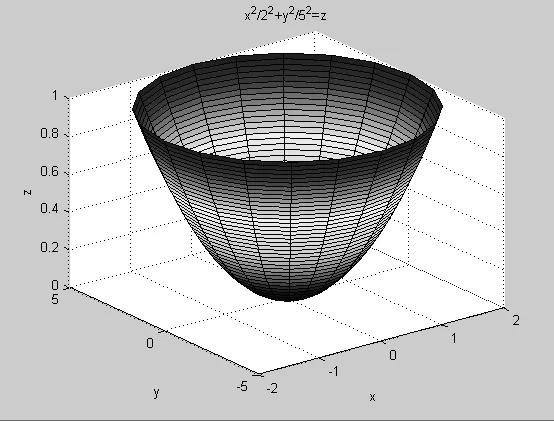
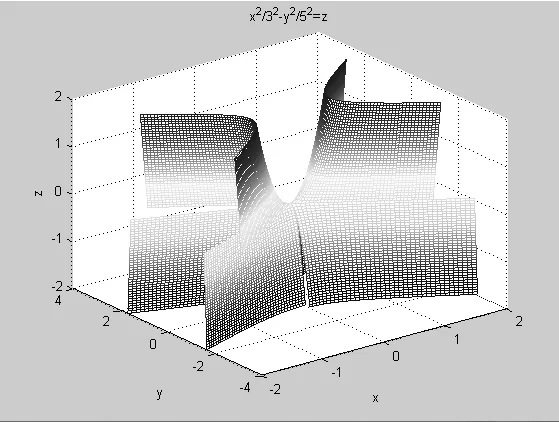
程序设计思路:首先生成x2+y2-(z+1)2=-1在(0 程序如下: 图5、图6给出a=3、b=4、c=5双叶双曲面的生成过程效果图。 图5 双叶双曲面(z>0) 图6 双叶双曲面 程序设计思路:首先生成曲面S:x2+y2=z,然后将S沿x、y轴方向伸缩a、b倍。得到椭圆抛物面 程序如下: 图7给出的是a=2、b=5的椭圆抛物面效果图。 图7 椭圆抛物面 图8 双曲抛物面 程序如下:图8是程序运行效果图。在 z<0 从上面的分析可以看到借助于MATLAB可以容易地实现空间解析几何二次曲面伸缩法的设计和演示,从而直观的、立体的和运动的揭示二次曲面的图像特征和方程之间的对应关系。这使得空间解析几何的教学增加了趣味性和生动性,也使空间解析几何课程的学习变得易于理解和巩固。 [1]度巍.空间解析几何中二次曲面截痕法的动画演示[J].电脑知识与技术,2011,(9)6297-9301. [2]李锐.现代教育技术与空间解析几何教学整合的研究[J].中国电力教育,2010(34)91. [3]林海涛,林海如.常用软件在空间解析几何教学中的实践[J].广东轻工职业技术学院学报2010,(9)33-36 [4]苏金明.MATLAB实用指南[M].电子工业2002. [5]同济大学数学系.高等数学[M].高等教育出版社2007.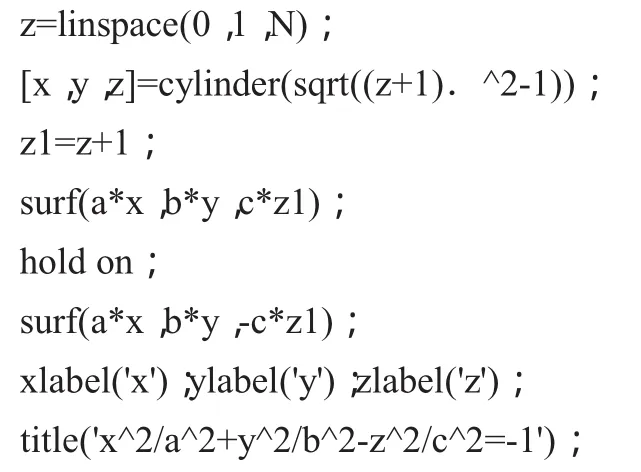


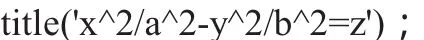
4.结束语
