基于Dijkstra和GIS的湖南省应急物流模型研究

谢金龙，武献宇

（湖南现代物流职业技术学院，湖南 长沙 410001）

应急物流是以提供突发性自然灾害、突发性公共卫生事件、战争等所需应急物资为目的，以追求时间效益最大化和损失最小化为目标的一种特殊的物流活动[1]。因此，应急物流以追求时间效益最大化和灾害损失最小化为目标，具有突发性、不确定性、非常规性、弱经济性等突出特点。

为了保证应急物资的调运、缩短配送时间、满足应急物资调运的时效性需求，应急物资调运信息系统具有重要的研究价值。目前对应急物资调运信息系统的研究工作大致可以分为两大类：（1）利用定性分析方法，研究应急物资调运信息系统构建的相关理论、系统概念模型的结构和功能模块分析，以及数据仓库、GIS等信息技术在应急物流信息系统中的应用等；（2）采用定量分析方法，通过数学模型分析，研究应急物资调运信息系统中的路径优化、物资分配、车辆优化调度等核心问题[2]。在目前的研究中，两大类别的研究工作相结合的文献并不多见，而本文在此方面进行了一定的探索。

针对应急物流的特点和需求，本文以湖南省区域物流为研究对象，提出了一种基于Dijkstra算法和GIS（Geographic Information System）的应急物资配送模型[3]，对应急物流调运中的优化路径选择问题进行探索和研究。

1 问题提出

在应急物流调运中，选取时间最短的运输路径是其中的核心问题。在实际应用中，主要包括距离最短，或时间最短、距离和时间的加权组合最短等问题[4]。

可以把交通网络抽象为一个赋权有 向图 G=（V，E，w）、V={vi|i=1，2， … ，n}为 交 叉 路口 构 成 的 点 集 ，E={eij|i，j1，…，n}为连接各交叉路口的边集 ，w 为 权 值 函 数 ，w （ei，j）表示边 ei，j的权值，如图 1所示。

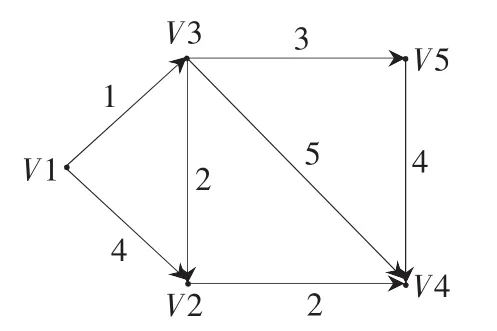
图1 节点间关系的有向示意图

2 研究基础

2.1 GIS系统

地理信息系统（GIS）是以地理空间数据库为基础，在计算机软硬件的支持下，对空间相关数据进行采集、管理、操作、分析、模拟和显示，并采用地理模型分析方法，适时提供多种空间和动态的地理信息，为地理研究和地理决策服务建立起的计算机技术系统[5]。将GIS等现代信息技术应用于应急物流中，可以实现应急物流系统的快速响应、准确定位和实时更新[6]。

GIS系统的功能：

（1）具有地图显示功能，通过空间属性信息查询可以了解备选区域的地理位置、地形、地貌，从而准确地确定应急物流配送点的位置及线路。

（2）GIS地图上，可以获得应急物流配送点和需求点的精确地理位置（用经纬度表示）。由于应急物流中心和需求点等空间实体已经数据化，所以能方便地得到物资运输地道路情况和运输条件，从而确定最优路径。

（3）GIS是一个动态的系统，具有良好的动态交互性，它强大的数据库系统可以保持数据的实时更新，地理空间上的任何变化，GIS都可以更新其数据库以备调用。同时，利用GIS的空间查询分析功能，在应急物流配送过程中能很好地实现时效性，以保证应急物流的实施。

Map Info Professional 7.0 SCP软件绘制的湖南省区域物流城市节点如图2所示。

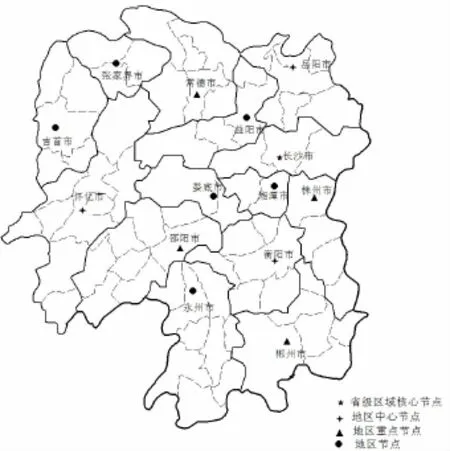
图2 湖南省区域物流城市节点示意

本文以Visual Basic和GIS软件MapInfo Professional 7.0 SCP作为开发工具，以长沙市为研究对象，利用MapX软件模拟实现一定区域内应急物流的配送，其系统功能图结构如图3所示。

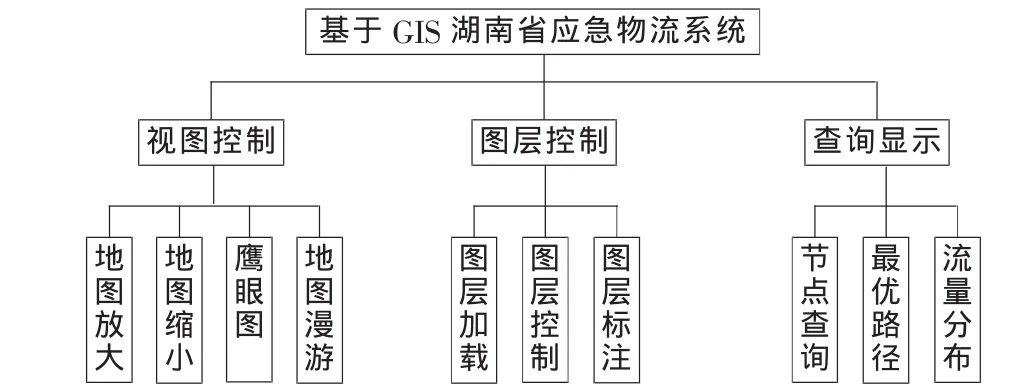
图3 系统功能结构图

2.2 算法实现

假定vs和vt分别为路径的起点和终点，路径集 Ps，t表示所有vs→vt的路径，路径p∈Ps，t的长度可以定义为：

其中，vi，j为构成路径p的每一条边。最短路径问题则可表示为求解节点序列 po=（vs，…，vt）使其满足：

Dijkstra算法是经典的单源最短路径算法[8]，其算法思想为：

（1）把V分解为两个子集S和T，初始状态时S={vs}，T=V-S；

（2）对于每 个 viI T 计 算 l（vs，vi），根据 l（vs，vi）的值找出 T中距 vs最短的节点 vx，并用 vs→vx的最短路径长度进行标记；

（3）设 S=S E{vx}，T=T-{x}， 若 T={f}，则 停 止 ；否 则重复（2）。

当算法执行完毕时，就可以求出起点vs到其余所有节点的最短路径。如果仅需要求vs到指定节点vt的最短路径，则在vt被从集合T中删除时即可退出算法，对节点标记过程进行回溯即可得到相关的路径。

3 仿真实验

某地区突发公共卫生事件，需要对各个医院运送药品，物资配送中心为该地某医药公司。位置已知，有8个医院需要紧急救援物资，物资种类有两种，每个医院编号以及需求量已知，各个需求点允许到达最晚时间已知。如表1所示，车辆运输速度为60 km/h，车辆数为5，车辆载重量为10 t，配送中心以及各医院间的距离如表2所示，配送中心对各医院送货，使每个医院在规定时间之内得到物资，同时使配送时间最短。

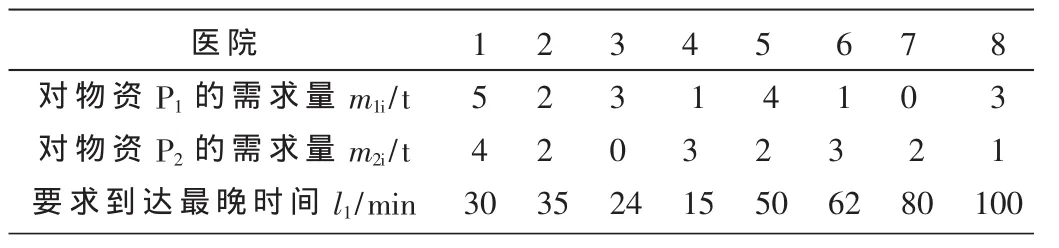
表1 各医院对物资的需求量

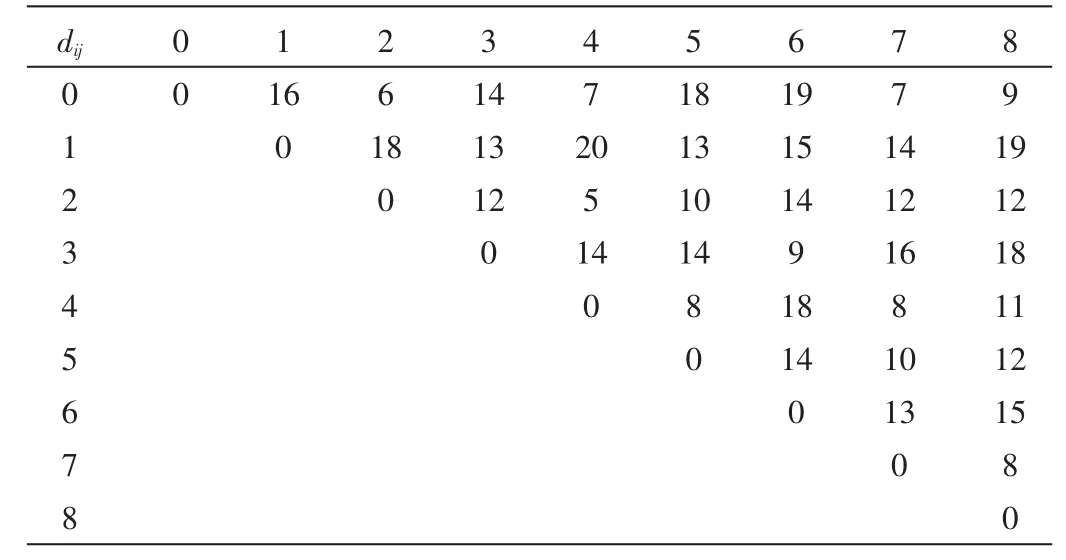
表2 配送中心到各医院的距离及受灾点间的距离/km

利用Dijkstra算法，采用Matlab 7.0编程对距离矩阵求解，得到 4条条路径为：1-5-3-1、1-2-1、1-9-6-1、1-4-7-8-1。

因为在编程时将配送中心定义为编号1，医院定义为编号 2～9，所以实际得出 4条路径为：第一辆车的配送路径为：配送中心-4-2-配送中心；第二辆车的配送路径为：配送中心-1-配送中心；第四辆车的配送路径为：配送中心-8-5-配送中心；第五辆车的配送路径为：配送中心-3-6-7-配送中心。

针对应急物流追求时间效益最大化、灾害损失最小化、灾害救援时间紧迫性等特点，本文提出的基于Dijkstra算法和GIS的动态优化路径选择方法能实现灾后应急物资调运路径的优化选择，较好地满足了应急物资调运的时效性需求，对实际应急物流的实施也有一定的参考价值。

[1]谢金龙，翟玲英，段圣贤.物流地理[M].北京：高等教育出版社，2011.

[2]谢金龙，刘亚梅，王凯.物流信息技术与应用[M].北京：北京大学出版社，2011.

[3]严寒冰，刘迎春.基于GIS的城市道路网最短路径算法探讨[J].计算机学报，2000（2）.

[4]汪定伟，张国祥.突发性灾害救援中心选址优化的模型与算法[J].东北大学学报，2005（10）.

[5]王占全，赵斯思，徐慧.地理信息系统（GIS）开发工程案例精选[M].北京：人民邮电出版社，2009.

[6]陈曦，傅明.GIS环境下物流配送中心选址模型与算法研究[J].计算机技术与自动化，2001（4）.

[7]Liu Houngzhi， Ou Jianjun， Li Wenzheng， et al.Research on public emergency rank.assesment based on BP neural network[C].The Second International Workshop on Education Technology and Computer Science，2010.

[8]Chang Meishiang， Tseng Yaling， Chen Jingwen.A scenario planning approach for the flood emergency logistics preparation problem under uncertainty[Z].Transportation Research Part E43， 2007.