基于Ridgelet变换的多尺度去噪算法研究*
2012-08-08侯振杰吕国玲张建华
王 梅,侯振杰,吕国玲,张建华
(内蒙古农业大学 计算机与信息工程学院,内蒙古 呼和浩特 010020)
Standford大学的CANDES E J于1998年研究了一种新的多尺度变换——Ridgelet变换[1-2]。Ridgelet变换的前身是小波变换,小波变换是处理非平稳信号的有力工具,与傅里叶变换相比前进了一大步,因此在信号处理中得到广泛应用。因此在二维图像中,图像的大多信息包含在边缘中,小波变换只能反映“过”边缘的特性,而无法表达“沿”边缘的特性。在小波变换基础上提出的多尺度Ridgelet变换不仅能有效处理高维情况下的线状奇异性,而且它以稳定和固定的方式用一系列脊波函数的叠加来表示一个具有多变量的函数类。在这些新的函数类上,利用各种特殊的高维空间的不均匀性来模拟显示信号。因此用Ridgelet变换来检测直线特征,不仅可以有效地捕获各个尺度、各个位置和各个方向上的信息,而且可以更稀疏地表示图像的多方向特征。
1 Ridgelet变换的基本理论
1.1 Ridgelet变换的定义
考虑多变量函数 f∈L1∩L2(Rn)。
若函数 Ψ:R→R属于 Schwartz空间 S(R),且满足容许性条件:

则称Ψ是容许神经激励函数,相当于小波函数。称式(2)为脊波函数。
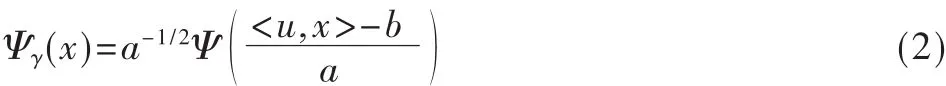
其中,γ 为三元组(a,u,b),γ∈Γ,参数空间 Γ={(a,u,b):a,b∈R,a>0,u∈s∈sn-i},sn-1为空间 Rn中的单位球,分别称a为尺度参数,b为位置参数,u为方向参数。
定义连续脊波变换为:

1.2 有限 Ridgelet变换(FRIT)
DO M N和VETTERLI M提出一种脊波变换的数字实现方法[3-4]——有限脊波变换FRIT(Finite Ridgelet Transform)。根据小波和Radon变换的关系,可以由有限Radon(FRAT)和小波来构建FRIT。FRIT是在FRAT(Finite Radon Transform)的基础上经一维小波变换得到的,FRIT是有限区域大小的二维实数离散信号实现脊波变换的离散手段,构建过程如下:
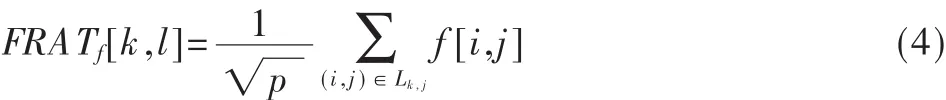
FRIT使脊波变换可以方便地在计算机上实现,而由于现在建立的FRIT是冗余的,DO M N和VETTERLI M提出了正交有限脊波变换来解决结果的冗余[4],Xia Junjun等提出了二进离散脊波变换[6]。
2 基于Ridgelet变换的图像去噪算法
Ridgelet变换可以更好地表征图像中的直线,对于分段光滑且沿直线边缘奇异性的图像来说,Ridgelet变换去噪既可以有效去除噪声,又较好地保留了特征。
假设噪声图像的模型为高斯加性噪声模型:

其中,x为原图像,n为高斯白噪声,y为含噪声图像。
以处理含有高斯白噪声的图像为例,在原始图像中加入标准差为σ的高斯白噪声,这里采用软阈值实现去噪,详细算法描述如下。
首先,对 n×n原图像进行预处理,得到k×k的图像(k是大于n的最小素数),对处理后的图像加噪声,加入均值为零、标准差为σ的高斯白噪声。一些常见的噪声有椒盐(Salt&Pepper)噪声、高斯噪声、脉冲噪声等。椒盐噪声含有随机出现的黑白强度值,而脉冲噪声则只含有随机的白强度值(正脉冲噪声)或黑强度值(负脉冲噪声)。与前两者不同,高斯噪声含有强度服从高斯或正态分布的噪声,而且在实际应用中,高斯噪声标准差只能通过中值估计方法近似估计:

其中,wij为Contourlet变换域预处理的系数,0.674 5为经验值。
其次,对含噪图像进行有限脊波变换(FRIT)。去噪的方法很多,由于阈值去噪[7]方法简单有效,因此应用十分广泛。在阈值去噪中,阈值的选取对去噪效果有着重要的影响。对于加性高斯噪声中的信号估计问题,DONOHO提出了软阈值去噪方法[8],用默认阈值对FRIT变换系数进行软阈值操作。软阈值方法处理的结果相对平滑,去噪效果非常明显,但是会出现“过扼杀”的现象,往往会造成图像边缘模糊、图像边缘细节等信息丢失的现象。通常,软阈值(soft)函数的公式为:

即软阈值把(i,j)处的脊波系数绝对值与指定阈值λk(i,j)相比较,小于阈值的点变为0,大于或等于阈值的点变为该点绝对值与阈值的差。在实验中采用“db4”小波,分解层数均为5层。
然后,对处理后的阈值系数进行逆FRIT变换得到去噪后的图像。
在不同尺度下,随着尺度因子的变化,图像的特征点的数量会发生变化,这里提及的“同一特征点”指的是同一目标源图像在不同尺度层下,经过滤波模糊化处理均能保留下来的那些特征点,从而在物质上保证了这些特征点的稳定性。本文中提出了一种基于尺度因子与Ridgelet变换的图像去噪算法,通过改变高斯截断函数中的尺度因子改变对图像的去噪效果。若尺度因子过小,则平滑程度降低,高斯截断函数图像变小,Wavelets的去噪效果优于FRIT;若尺度因子过大,则平滑程度提高,高斯截断函数图像变大,FRIT比Wavelets的去噪效果更有效。所以随着尺度因子的变化,FRIT和Wavelets的去噪效果也发生着变化。
本实验用图片的高斯截断函数作为对比图,高斯曲面阈值方法是将高斯滤波后的图像作为阈值面对原图像进行分割的一种方法[9],可以很好地抵制灰度不均和噪声对图像的影响。二维高斯截断函数为:
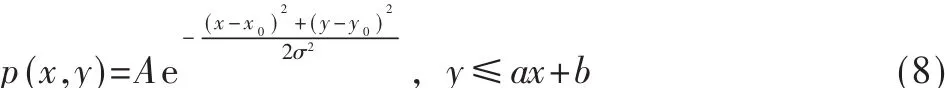
在概率中,以式(8)为基础的高斯分布形式为:
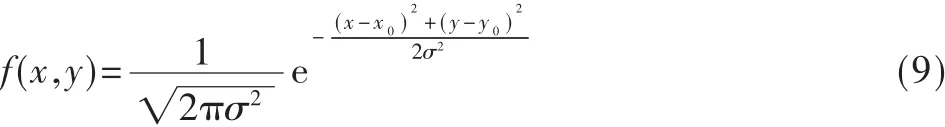
其中,x0为均值,σ2为方差。式(9)反映了高斯分布的离散程度,就高斯曲线而言,象征着曲线的宽度。
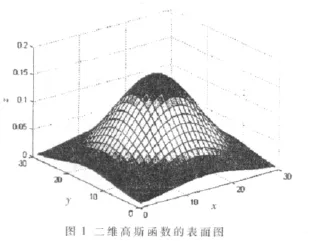
二维高斯函数的曲面形状如图1所示。由于图像可以看作是一个离散的数据矩阵,因此对图像平滑通常都采用函数模板对图像进行卷积处理。
在图像处理中,去噪的目标是最小化均方误差(MSE),通常利用归一化均方误差(MSE)和信噪比(SNR)作为去噪效果的评价指标。归一化均方误差定义为:

其中,m、n为图像大小。
图像的信噪比定义为:
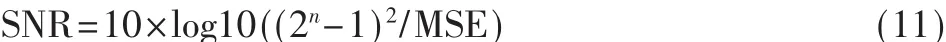
其中,n为每个采样值的比特数。
3 实验结果与讨论
本文实验采用257像素×257像素的obj图像作为测试图像,先对obj图像应用高斯截断函数,对高斯截断函数图像加均值为零的不同强度(噪声标准差σ)的高斯白噪声,以及在不同尺度因子下对含有相同噪声图像的去噪。尺度因子是高斯截断函数的一个重要参数,尺度因子的变化直接影响图像的变换,从而影响去噪效果,因此尺度因子的变换也影响到图像的去噪效果。实验采用SNR作为客观评价指标。不同噪声强度下用不同去噪方法去噪后图像的SNR值如图2和表1所示。相同噪声(σ=0.335,噪声=13.95)不同尺度因子去噪效果如图3和表2所示。

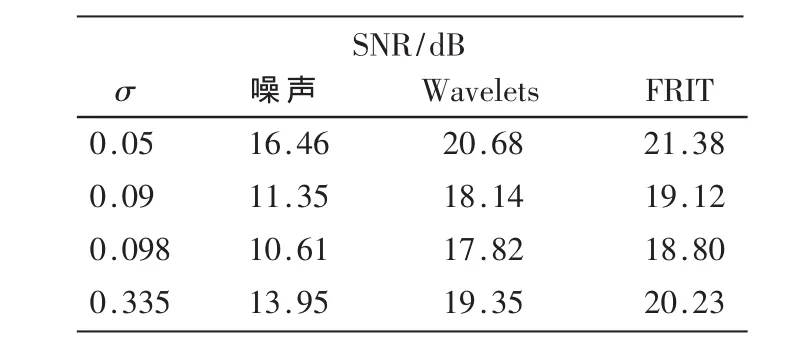
表1 两种去噪方法的恢复图像的SNR值
由图2和表1可知,对obj图像的高斯函数进行图像去噪,采用Wavelets去噪后的图像比较模糊,采用FRIT去噪后的图像明显清晰许多,从信噪比上看,FRIT也明显高于Wavelets的结果。
由图3和表2可知,用图片的高斯截断函数作为对比图,对高斯函数中尺度因子的改变不仅影响图像的大小而且影响去噪效果。在相同噪声的情况下,当尺度因子在一定范围内,FRIT优于Wavelets的去噪效果,但是如果尺度因子超出范围,这种去噪就会失去应有的效果。
本文介绍了Ridgelet变换的基本原理及其在图像降噪中的应用。实验结果表明,对于具有直线状特征的模型,高斯函数中尺度因子在一定范围内,Ridgelet方法比Wavelet方法具有更好的去噪效果。然而自然图像的边缘通常不一定是直线型的,具有曲线奇异性,对于曲线状特征的图像,Ridgelet变换就满足不了要求了。因此Ridgelet变换有待于进一步提高,可选择合适的理论与脊波变换相结合应用于图像处理,以弥补Ridgelet变换的不足。

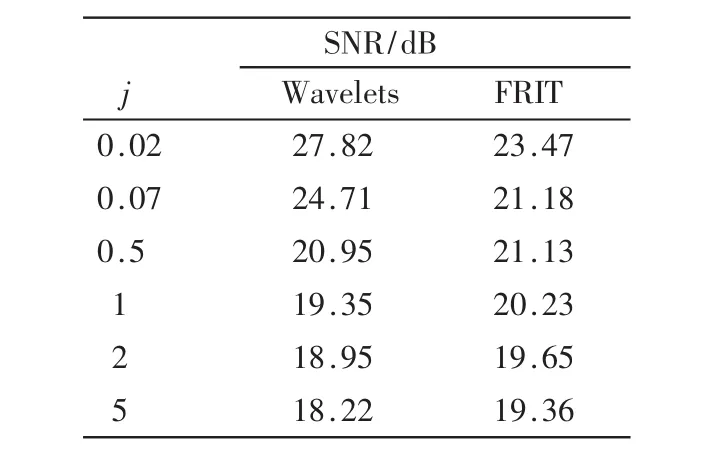
表2 相同噪声不同尺度下两种去噪方法的对比
[1]CANDES E J.Ridgelets and their derivatives:representation of images with edges[R].Department of Statistics,Standford University.
[2]CANDES E J.Harmonic analysis of neural networks[J].Applied and Computation Harmonnic Analysis,1999(6):197-218.
[3]DO M N,VETTERLI M.The finite ridgelet transform for image representation[J].IEEE Transactions on Image Processing,2003,12(1):16-28.
[4]DO M N,VETTERLI M.Orthonormal finite ridgelet transform for image compression[C].IEEE International Conference on Image Processing,ICIP-2000,2000.
[5]舒正华,邹道文,汪胜前.基于有限脊波变换域的图像水印技术[J].计算机与现代化,2007(3):35-37.
[6]Xia Junjun,Ni Lin,MIAO Y.A new digital implementation of Ridgelet transform for images of dyadic length[C].Proceedings of the Third International Conference on Information Technology and Applications(ICITA’05),IEEE Computer Society,2005.
[7]DONOHO D L,JOHNSTONE I M.Ideal spatial adaptation by wavelet shrinkage[J].Biometrika 1994,81(3):425-455.
[8]DONOHO D L.De-noising by soft-thresholding[J].IEEE Transactions on Information Theory,1995,41(3):613-627.
[9]朱虹,许朝晖,周健.基于PCR凝胶成像的信息自动提取[J].中国图 象 图 形学报(A 版),2002,7(12):1285-1290.
