输水管道水力损失的计算及其影响因素分析

王中 陈卓

(湖北职业技术学院建筑技术学院，湖北孝感 432000)

计算水流在经过管道时所产生的水力损失是给排水工程中常见的一个问题。在实际的工程计算中，沿程水头损失一般按照水力学书或水力手册中的公式进行计算，较为简单，但公式较多，如何选用最佳的计算公式关系到工程设计方案在运行中的经济性问题。精确的计算水力损失对选泵问题以及水锤的防护控制措施有重要影响，是确定方案可行性和经济性的一个十分重要的步骤。

1 计算水头损失公式

1.1 水头损失常用公式

1)达西公式

式中:λ为沿程水头损失系数，L为所求的沿程的距离，v为管道内的平均流速大小，R管道的水力半径，g为当地重力加速度。

2)谢才公式

常用于沿程水头损失的公式还有谢才公式:

或者

式中:Q为管道流量，ω为过流断面的面积，c称作谢才系数，R管道的水力半径，J为水力坡度。

3)舍维列夫公式

对于新钢管，

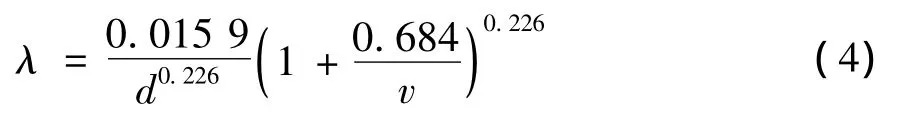
此式使用条件为Re＜2.4×106d，d以m计。对于新铸铁管，

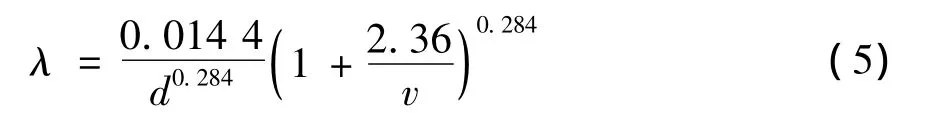
此式使用条件为Re＜2.7×107d，d以m计。

对旧铸铁管及旧钢管(使用2个月以上)，当V＜1.2m/s，

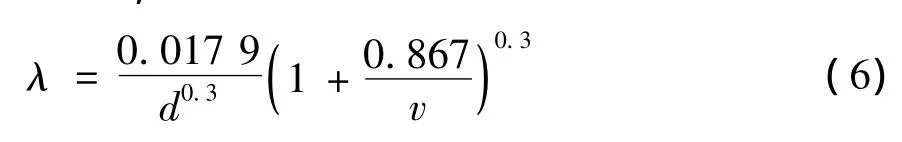
当管材为旧钢管、旧铸铁管，其水力计算公式也可以根据流速的判别，采用下列的舍维列夫公式:

V≥1.2m/s时

当V≥1.2m/s，

V＜1.2m/s时

4)海森威廉公式

表1 种管道在管材100 m时四种公式计算值对实验值的比较

式中:Q为管道流量，l为管道长度，Ch[18]为海森威廉系数，d为管道直径。

1.2 管道沿程水头损失计算公式的比较与选用

选用参数:水的物理化学参数以20℃、大气压为101 kPa的条件下取值，其中密度ρ=999.73 kg/m3。计算结果如表2～4。

达西公式:υ为水的运动粘性系数，m2/s.水温20 ℃时，υ =1.01×10－6m2/s.Re=vd/υ，布拉休斯修正公式 λ =0.312/Re0.239。

海森威廉公式:Ch=135

谢才公式:巴氏公式c=(1/n)Ry，n=0.009，y—指数，可按巴浦洛夫斯基公式进行计算，可简化为公式当R＜1 m/s时，y=1.5，R＞1m/s时，y=1.3，计算结果如表1所示。

用Origin软件生成图1

图1 四种公式计算结果与实验值的比较

由表1数据通过方差比较，可以看出，谢才公式和海森威廉公式对实验值误差都较小，但海森威廉公式计算的误差更小，在实际工程中，计算水力损失比谢才公式计算精确。

沿程水头损失计算公式都是在一定的实验基础上建立起来的，由于实验条件的差别，各公式的适用条件和计算精度也会有所不同。根据上述对各个公式的分析，现比较如下

(1)谢才公式和达西公式为管渠水力计算的经典公式，己经成为给水排水网水力计算的基本公式，谢才系数C和达西阻力系数λ的科学计算和应用是管水管网水力损失计算正确性的关键。

(2)海曾一威廉公式特别适用于给水管网的水力计算，该公式可用于短距离输水，但用于长距离输水准确度更高，应用广泛，具有较高的计算精度，很多编程软件都是以海曾一威廉公式来进行编程。

(3)舍维列夫公式是通过旧钢管旧铸铁管试验资料确定的，而现在国内采用的金属管道已普遍采用水泥砂浆和涂料做内衬，条件已经发生了变化，所以该公式目前也已基本不再使用。

2 管道沿程水头损失计算的影响因素

2.1 管道管材对水头损失的影响与计算

目前我们的给排水管材主要包括金属管和非金属管，金属管材主要有镀锌钢管，铸铁管，而非金属管材主要有混泥土管，钢筋混凝土管，塑料管，以及复合塑料管等。

本文讲通过计算，来说明不同管材对水头损失的影响，并比较其误差

取钢管沿程水头计算为例，计算钢管均匀流沿程水头损失的基本公式为达西公式

公式中g—重力加速度，9.81m/s2。

根据舍维列夫进行的钢管及铸铁管的实验，提出了计算过渡区及阻力平方区的阻力，新钢管

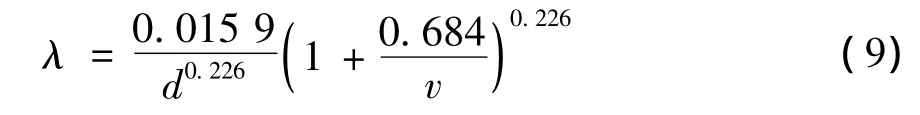
在计算时，我们统一水温是在0℃的情况下进行计算，当水的运动粘滞度1.78×10－6m2/s的条件下代入公式计算，由公式可以简化得出，

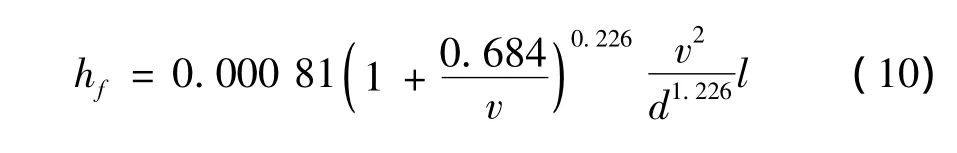
当假设管道距离长为1 000m的时候，可得计算结果如表2。

表2 新钢管水力损失计算结果

塑料管沿程水头计算为例，以PE的水头损失计算。根据达西公式，塑料圆管沿程水头损失hf同样应按下式计算:

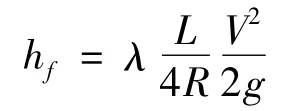
因在通常的流速条件下，常用给水管PE管一般处于水力光滑区，管壁绝对当量粗糙度对结果的影响非常小，故水力粗糙系数系数 λ可按下式计算:

雷诺数Re应按下式计算:

式中υ—水的运动粘滞度(m2/s)，在不同温度时可按表3采用。

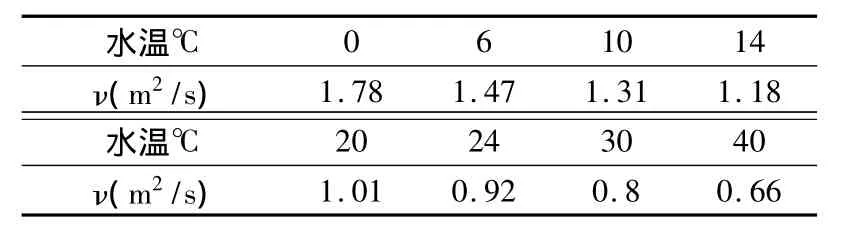
表3 水在不同温度时的υ值(×10－6)

在上述同样条件下，由公式简化得出，

当假设管道距离长为1 000m的时候，可得计算结果如表4。

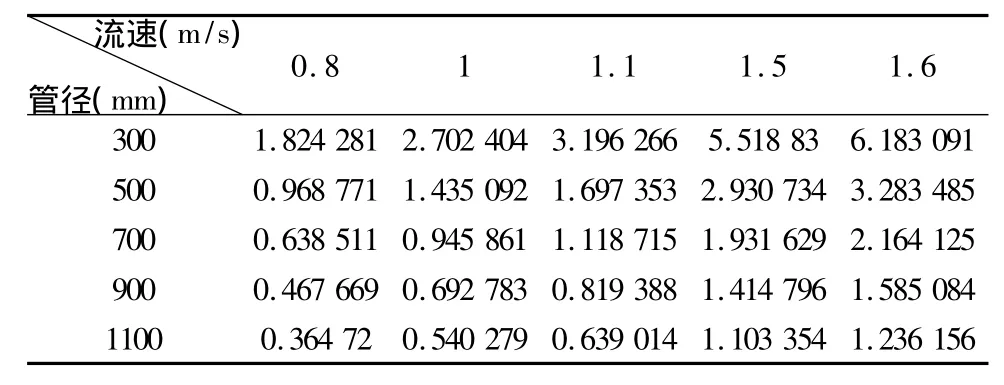
表4 PE 管水力损失计算结果

由计算可以看出，塑料管的沿程水头损失小于金属管的水头损失，这是由于PE内壁粗糙度一般比钢管，铸铁管要小，PE管光滑的表面和非黏特性降低了管路的压力损失和输水能耗。管道粗糙度差异，对输送能耗的影响则显得尤为突出[1]。在一般实际工程设计中，在允许流速范围内，相同内径不同管材由于其表面粗糙度不同，在同一流速下其管内水流完全可能处于不同的紊流状态，故而对水力计算经验公式造成误差，在长距离输送管道上，计算结果误差会大大增加，而导致比较严重的后果。

2.2 管道管径及对水头损失的影响与计算

对于对给定的流量，管径的大小与管道系统的一次投资费(材料和安装)、操作费(动力消耗和维修)和折旧费等项有密切的关系，应根据这些费用做出经济比较，以选择适当的管径。此外，管径的大小还对沿程水头损失造成影响，如果忽略这种影响，可能会对系统的安全造成隐患。通过各个公式的计算，研究管径对水损造成的影响。

计算过程如下:

选用参数:采用PVC-U管材[2]公称压力PN=1.0MPa，管长 L=1 000m，水的物理化学参数以20℃、大气压为101 kPa的条件下取值，其中密度ρ=999.73kg/m3。计算结果如表2～4。

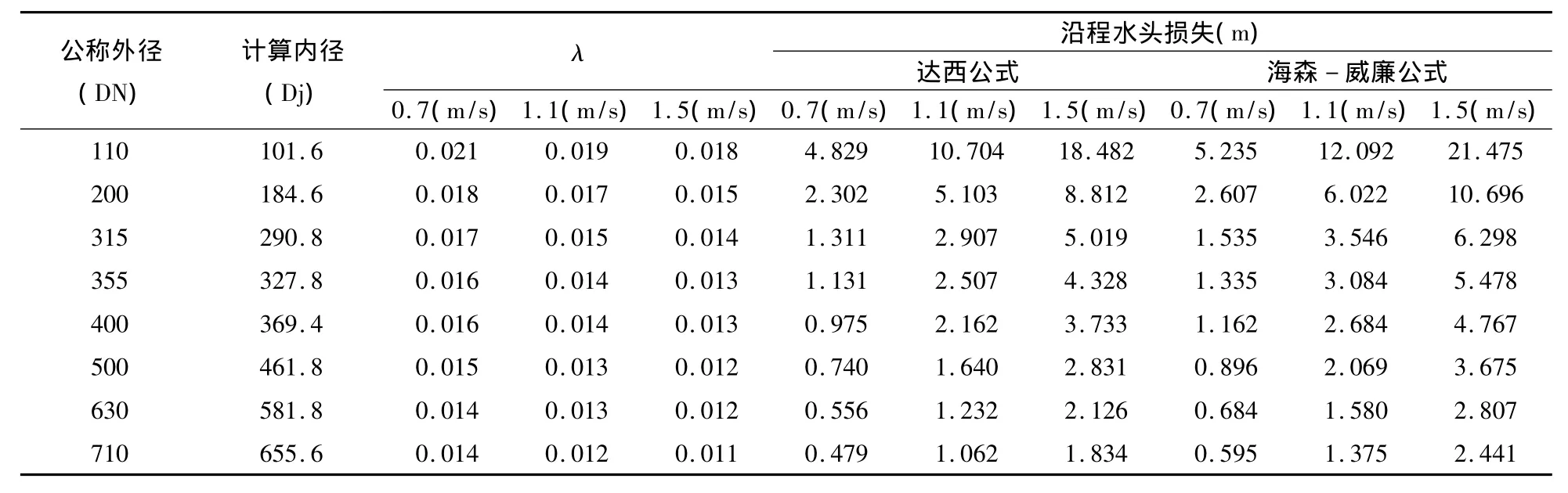
表5 达西公式与海森—威廉公式计算结果

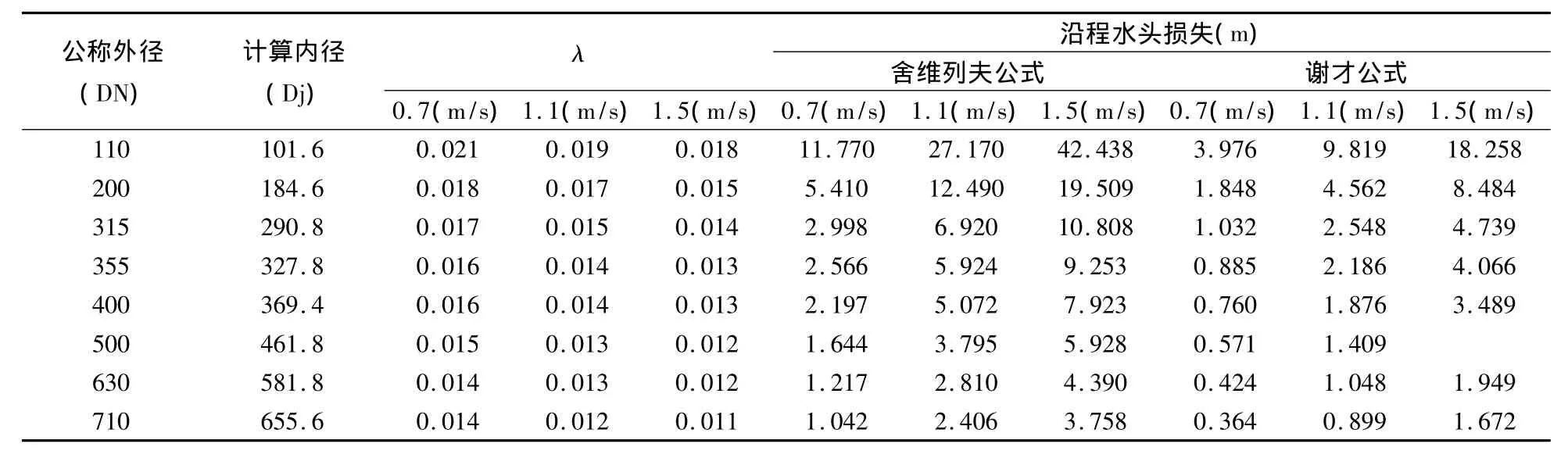
表6 舍维列夫公式与谢才公式计算结果

达西公式:υ为水的运动粘性系数，m2/s.水温20 ℃时，υ =1.01×10－6m2/s.Re=vd/υ，布拉休斯修正公式 λ =0.312/Re0.239。

海森威廉公式:Ch=135

达西公式计算生成的图2:

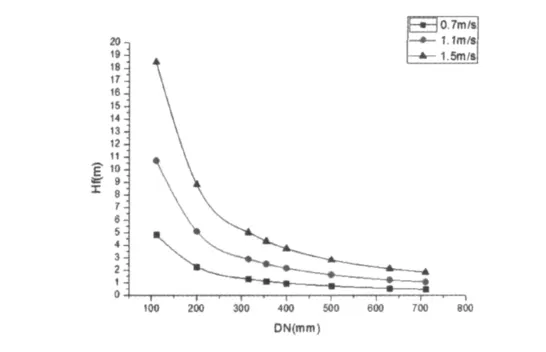
图2 达西公式随管径计算变化图

谢才公式计算沿程水头损失随管径的变化如图3:

谢才公式:巴氏公式c=(1/n)Ry，n=0.009，y—指数，可按巴浦洛夫斯基公式进行计算，可简化为公式当R＜1 m/s时，y=1.5，R＞1 m/s时，y=1.3，计算结果如表5、表6所示。

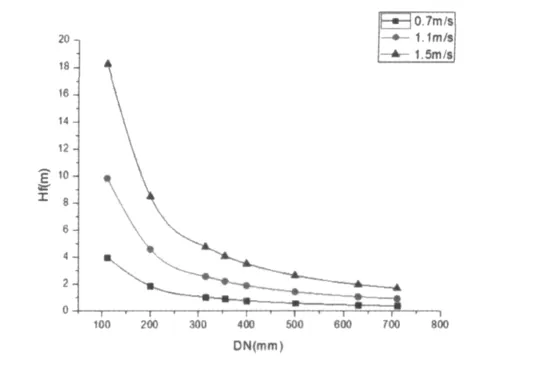
图3 谢才公式随管径计算变化图

舍维列夫公式计算沿程水头损失随管径的变化如图4:

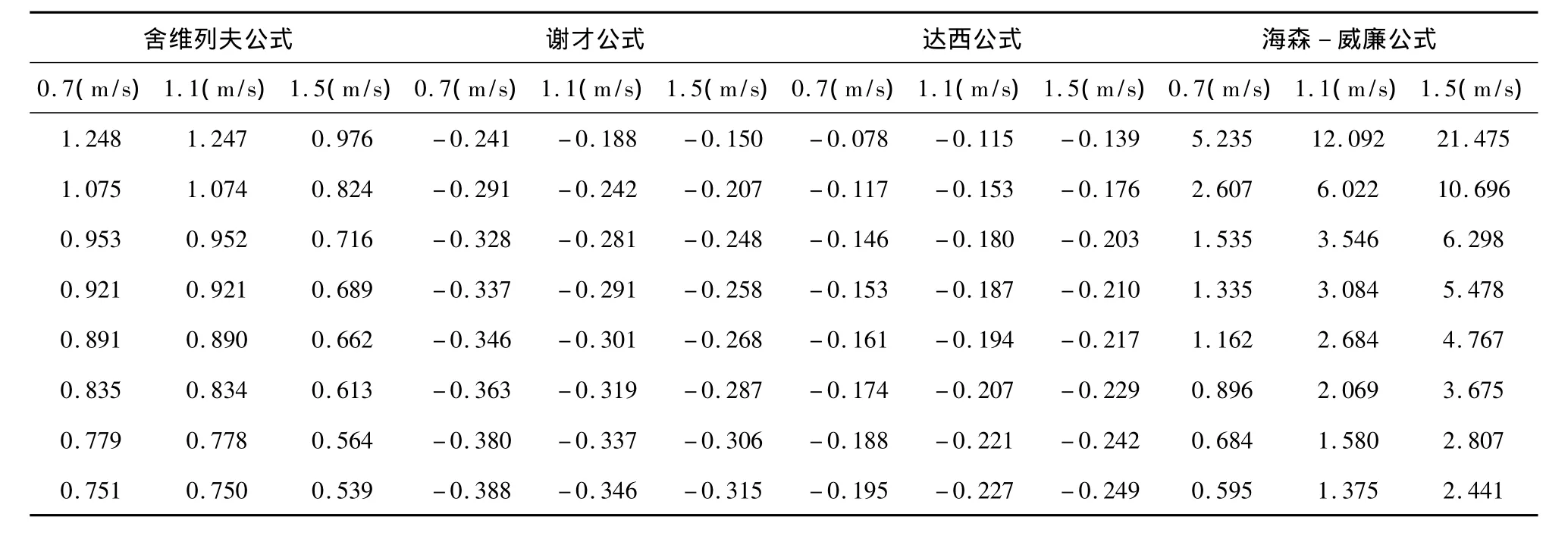
表7 其它三种公式跟海森威廉公式的相对误差表

图4 舍维列夫公式随管径计算变化图

海森威廉公式计算沿程水头损失随管径的变化如图5:

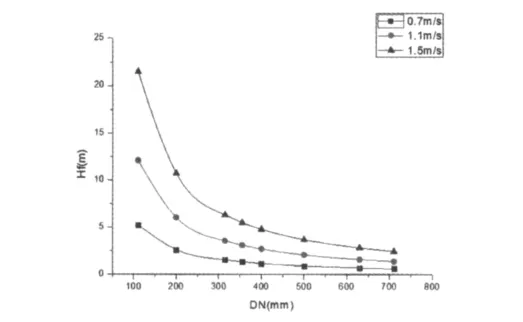
图5 海森威廉公式随管径计算变化图

由上面的计算可以知道，海森威廉公式计算水力损失值比其它公式计算误差值要小，在管径的变化下，计算其它三种公式跟海森威廉公式的相对误差见表7。舍维列夫公式计算的相对误差生成图表如图6:

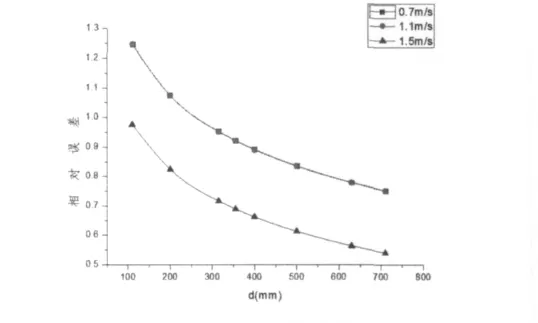
图6 舍维列夫公式计算的相对误差图

谢才公式计算的相对误差生成图表如图7。

图7 谢才公式计算的相对误差图

图2～10说明，谢才公式随管径变化的计算相对误差在流速大的时候高于流速小的时候。

达西公式计算的相对误差生成图表如图8。

图8 达西公式计算的相对误差图

计算结果分析

由图表估算管径不同所选用公式与海森威廉公式的误差。可以看出相对误差都是在管径变大的情况下，而相对误差却减小。

(1)当不存在水流流态改变的时候，海森威廉公式计算影响参数少，所以计算结果安全性高，通过对计算结果分析并结合《室外给水设计规范》对输水管道合理的经济流速的规定，设计中管道沿程水头损失计算建议采用海森一威廉公式。

(2)达西公式与海森-威廉公式均为半经验公式，其中达西公式需要考虑管中水流的流态，而水流的流态跟水的温度及管材粗糙度等因素都有关，跟用达西公式计算沿程水头损失的时候，需要考虑水流的温度管材粗糙度等因素的影响;海森-威廉公式只考虑管材粗糙度对沿程水头损失的影响，所以当系统中存在热交换设备时，或在冬季运行时，摩阻系数发生变化，采用达西公式计算较为准确，如果选取海森-威廉公式会有较大的误差。

(3)由于三种公式都是在管径增大的情况下相对误差减小，所以在计算管径小的时候要特别注意公式的选择问题，否则，会造成水力计算值跟实际情况严重不符的情况。

2.3 流速及对水头损失的影响与计算

由达西公式，可知，流速越大，hf越大，反之，流速越小，hf越小。现以新铸铁管运用达西公式计算为列来进行说明，查舍维列夫公式可得新铸铁管水力粗糙系数系数L取值为1 000m，现计算结果如表8。

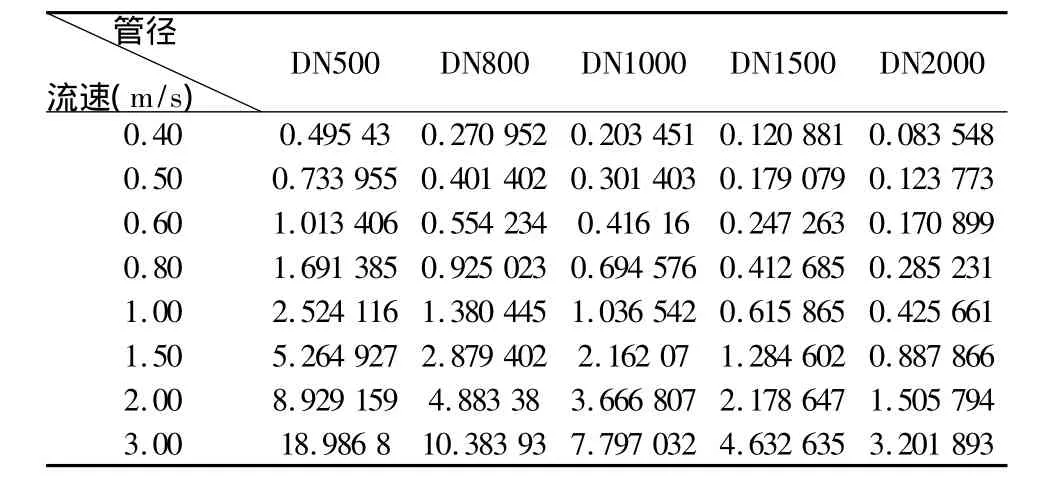
表8 流速及对水头损失的计算比较

用图9表示如下:

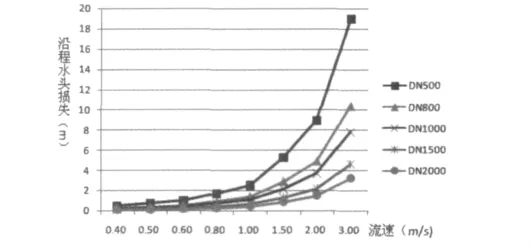
图9 不同直径下流速与每千米水头损失关系曲线

2.4 其他影响因素

管道的接口形式[3]，水温等其它因素也会对水力损失的计算造成影响。管道接口形式处，由于连接形式的改变而导致水流的流速，水流的状态发生改变而导致的水力损失一般为局部水头损失，工程中有许多管道系统如水泵吸水管等，局部损失占有很大比重。因此，了解局部损失的分析方法和计算方法有着重要意义。液体流经突变处，因突然扩大、突然缩小、转弯、分岔等缘故，在惯性的作用下，将不沿壁面流动，而产生分离现象，并在此局部形成旋涡，局部水头损失产生的主要原因是旋涡的存在，旋涡形成是需要能量的，此能量是由流动所提供的。在旋涡涡区内，液体在摩擦阻力的作用下不断消耗能量，而液体流动不断地提供能量，这是产生水头损失的主要原因。另外，流动中旋涡的存在使流动的紊流度(紊流强度)增加，从而加大了能量的损失。实验结果表明，流动突变处旋涡区越大，旋涡的强度就越强。局部水头损失就越大，从而使得沿程水头损失也越大[4]。水温的影响主要表现在其对雷诺数的影响方面上，可知计算:

式中υ—水的运动粘滞度(m2/s)，在不同温度时可按下表采用不同的值，当取管长为1 000 m，管径为110 mm 计算，不同水温在流速 0.7 m/s，1.1 m/s，1.5 m/s计算下水力损失数值如表9。

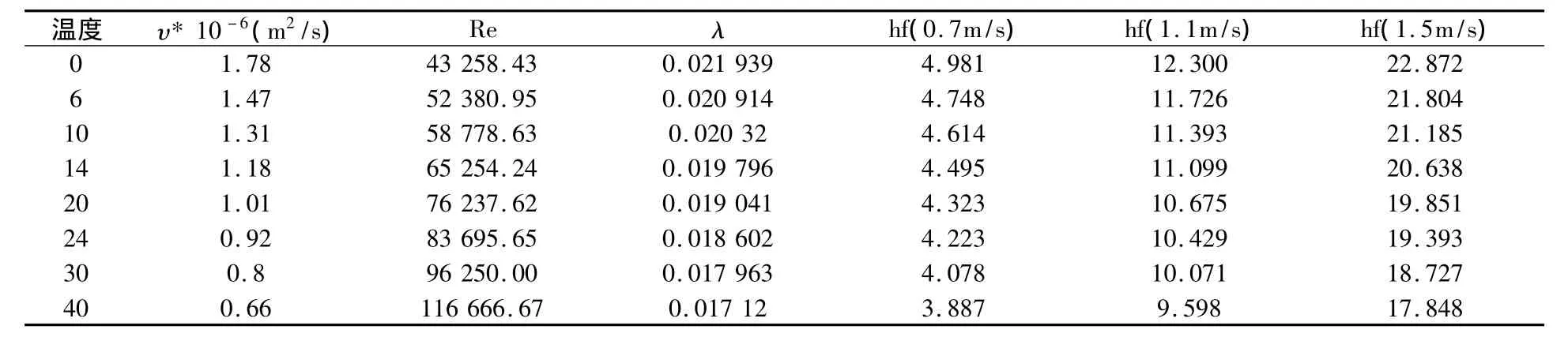
表9 不同水温对水头损失的计算比较

由表9计算可以看出可见水温越高，水力损失越小。

3 结论

由上述计算对比分析，可以看出，管径和流速的变化对沿程水头损失的改变影响较大:在其他条件一定的情况下，管径越大，沿程水头损失就越小。流速越大，沿程水头损失也越大。由于管材的改变对管材的粗糙度的影响很大，导致水头损失计算存在误差[5]。除此之外还有因为管道连接形式的改变，以及水温的改变都会对水力计算造成误差，在实际的计算工程中，我们要留意外界情况的细微改变，然后选择理想的计算公式，这样才能精确的计算水力损失的值。

长距离输水管道由于输送距离长，减小沿程水力计算的误差是优化设计的重要内容，根据选用管材的不同、管道口径的差异等设计条件，应对管道的水流状态进行辨别，避免超越水力计算公式的适用范围[6]。

水头损失的变化对水锤的影响也较大，而在工程实际中，水锤的防护措施的研究往往是工程所要研究的重点内容[7]。

[1]沈致和.给水管网水力计算及优化设计研究[J].给水排水，1997(1):62.

[2]卞启良，胡泽敏.UPVC给水管的水力计算公式[J].建筑技术通讯(给水排水)，1990(3):2-4.

[3]苏军.给水管道接口形式的选择及注意的问题[J].科技信息，2010(20):330.

[4]景江红.旁路局部损失对管网水力计算影响的研究[D].重庆大学，2005.

[5]陈涌城，杜玉柱，耿安锋.输配水管道沿程水头损失计算方法探讨[J].给水排水，2009(11):109-111.

[6] B W E.Simulation of vaporous and gaseous cavitations[J].Journal of Fluid Engineering，1984.

[7]兰景玲.长距离多起伏输水管道水锤防护研究[D].长安大学，2009.