K-TIG焊接电弧特性的数值分析
2012-08-06张瑞华栗海霞冷小冰
张瑞华 ,栗海霞 ,李 明 ,王 荣 ,冷小冰
(1.兰州理工大学甘肃省有色金属新材料省部共建国家重点实验室,甘肃 兰州 730050;2.苏州工业园区华焊科技有限公司,江苏 苏州 215021;3.中山职业技术学院,广东 中山 528404)
0 前言
近年来在国外兴起了一种新型高效的焊接技术——K-TIG焊接法,所谓的K-TIG(Keyhole TIG Welding)焊接法就是在传统TIG焊接的基础上,通过大电流(大于300 A)形成的较大电弧压力与熔池液态金属的表面张力实现相对的平衡,形成小孔实现深熔焊接[1]。最大单道焊接厚度可以达到16 mm,不需要开破口,焊接速度达到300~1000 mm/min,焊缝的微观组织和力学性能优于TIG焊[2-4]。目前对K-TIG焊的电弧行为特征研究还很少,数值模拟的研究更是未见报道。国内除了苏州工业园区华焊科技有限公司外,还未见其他机构研究该焊接技术。K-TIG焊接电弧行为特性(包括电弧压力、电流密度和温度等)会直接影响到焊缝的组织和性能。由于实际焊接时高温、高电流密度和强烈的弧光干扰,很难通过实验直接观测到电弧的行为特性[5]。在此采用数值模拟的方法研究了K-TIG焊大电流时的电弧特性,对于焊枪设计、焊接过程控制和焊缝质量评价都具有理论指导意义。
1 数值模型
1.1 基本假设
对K-TIG焊接电弧数学模型中进行了假设:电弧等离子体处于局部热平衡状态;电弧等离子体具有光学薄层特性;浮力和粘性热耗散忽略不计;电弧处于不可压缩状态的。
1.2 控制方程组
焊接电弧是一种带电的流体,可用流体动力学和电磁学相结合的方法来分析研究,控制方程组如下[6-7]:
质量连续方程

式中 u、v、w 分别为 x、y、z方向的速度;ρ为气体密度;κ为热传导率;μ为粘度;P为气体压力;T为温度;Cp为定压比热容;Sx、Sy、Sz分别代表动量方程在x、y、z方向的源项;SH为能量方程的源项。
电流连续方程

麦克斯韦方程
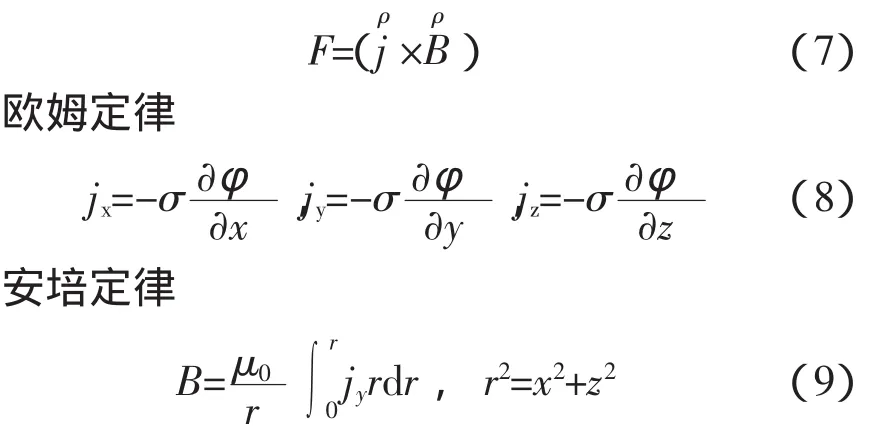
式中 φ为电势;F为电磁力;σ为电导率;μ0为真空磁导率,μ0=4π×10-7。
1.3 边界条件
依据苏州华焊科技有限公司提供的焊枪(见图1)建立物理模型。由于对称仅给出一半模型进行计算(见图2),该模型包括焊枪内部保护气体流动区域、钨极区和电弧区三个部分。其边界条件如表1所示。
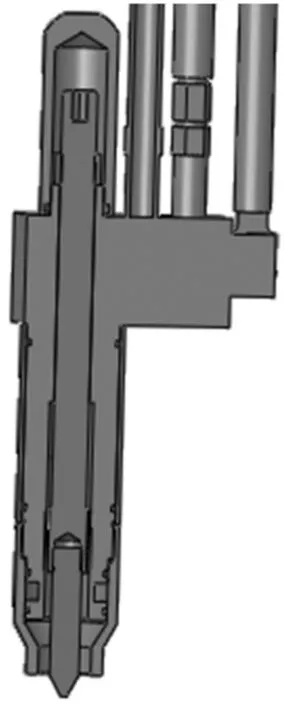
图1 K-TIG焊枪Fig.1 K-TIG welding torch
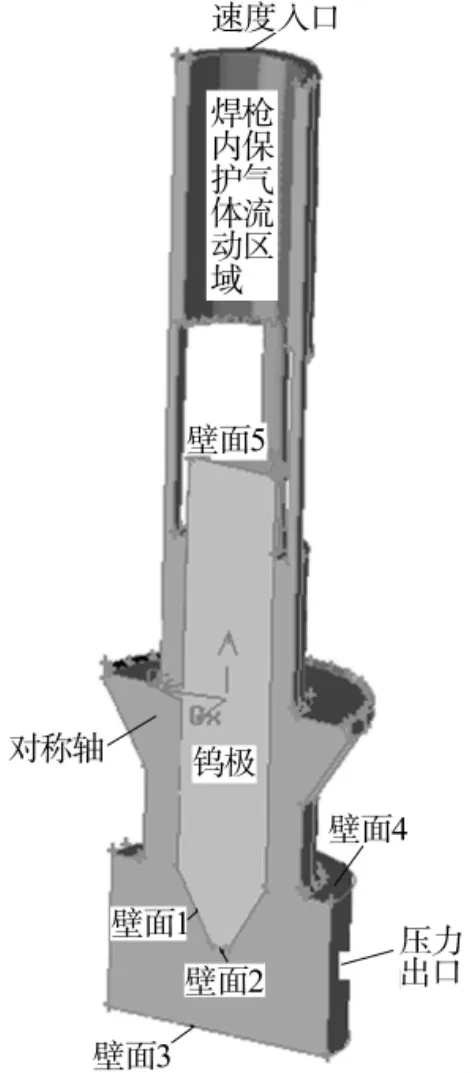
图2 计算模型Fig.2 The geometry model
对称面为绝热边界条件,其他面的温度为1000 K,整个计算模型区域内温度赋值为1000 K,弧柱区的温度赋值为10000 K。

表1 计算模型边界条件Tab.1 Boundary conditions of the geometry model
2 模拟方法
用前处理软件Gambit对焊枪和电弧建模并划分网格。取钨极尖端锥角为60°,直径为10 mm,钨极顶端半径1 mm,弧长9 mm,保护气体流量40 L/min。保护气体为氩气,其热物理性质参数是随温度变化而改变的[8]。
由于焊接电弧温度场和流场分布不均匀,为了保证计算结果的精度,在阴极端部和电弧中心等较为敏感的部位网格划分较密,采用将非结构网格和适应性网格相结合构成的混合型网格来划分几何模型。使用局部网格自适应功能对Gambit导入的网格进行局部二次精细化,从而提高了建立网格的效率,如图3所示。

图3 有限元模型的网格划分Fig.3 Mesh generation employed in the geometry model
3 模拟结果和分析
焊接电流为800 A时的K-TIG焊接电弧温度场分布如图4所示。800 A时钨电极前沿温度最高可达32000 K,阴极和阳极前沿温度梯度较大,电弧中心轴线上的温度分布较为均匀,温度场从阳极到阴极区逐步扩大,温度逐渐降低,温度变化梯度减小。电弧高温部分(T>10000 K)分布呈圆锥形。不同焊接电流条件下电弧温度沿电弧轴向的分布情况如图5所示。由图可知,随着电流的增大,轴线上电弧温度升高,但二者增加的关系不是线性关系。电流增加时,弧柱半径增大较快。

图4 I=800 A时电弧温度场分布Fig.4 Distributions of the temperature while I=800 A

图5 轴线上电弧温度分布Fig.5 Axial distributions of the temperature
电弧电势分布如图6所示。本研究采用直流反接,焊接电流800 A,工件接地为0 V,电极电势14.3 V。焊接电流为 500 A、800 A、1000 A 时在靠近电极附近都存在较大的电极压降,1000 A时电势的变化最为明显,随后电势变化趋于平缓,如图7所示。
焊接电流为800 A时电弧等离子体速度场分布如图8所示。等离子体首先沿钨极尖端斜面向内、向下运动,在电磁力作用下形成高速等离子流,最高速度达到730 m/s,当等离子体流到达工件时,受到阻滞作用,气流沿径向向外运动。高速运动的粒子将其动能传递给工件,对工件表面产生冲击力,即电弧压力。随着焊接电流的增大,轴向上的等离子体流速度增大,如图9所示。

图6 I=800 A时电弧电势分布Fig.6 Distributions of the potential

图7 轴线上电弧电势分布Fig.7 Axial distributions of the potential
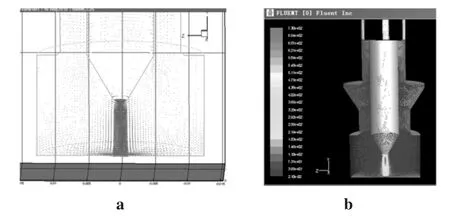
图8 电弧等离子体速度场分布Fig.8 Distributions of the plasma velocity

图9 轴线上等离子体速度分布Fig.9 Axial distributions of the plasma velocity
电弧压力等压线如图10所示,电弧的阳极区和阴极区分别呈现较高的压力,而远离这两个区域,压力相应减少。图11与图12a是焊接电流对电弧压力的影响。在弧长不变的情况下,随着焊接电流的增大,工件表面的电弧压力峰值增大。弧长为9 mm,当焊接电流从500 A增加到1000 A时,工件表面的电弧压力峰值从290 Pa升高到2060 Pa。可见K-TIG大电流焊接的一个显著特点就是工件表面的电弧压力较大,其主要是由电磁力和等离子流对工件表面的冲击引起的。K-TIG焊适合应用于焊接低密度或较低传导率的金属,其纯金属在熔点下的表面张力γ<2500 Pa。焊接过程中,较高的电弧温度可迅速将焊件的焊缝处金属加热到熔化状态,高速等离子流形成的较大电弧压力把熔融的金属压向四周,形成一个小孔,当电弧压力与液态金属的表面张力实现相对的平衡,小孔稳定。因此,电弧压力是小孔形成和保持稳定的关键因素。图12b说明在焊接电流不变的情况下,工件表面的电弧压力随弧长的缩短而增大,且峰值半径减小。

图10 电弧压力分布Fig.10 Distributions of the arc pressure
4 结论

图11 轴线上电弧压力分布Fig.11 Axial distributions of the arc pressure
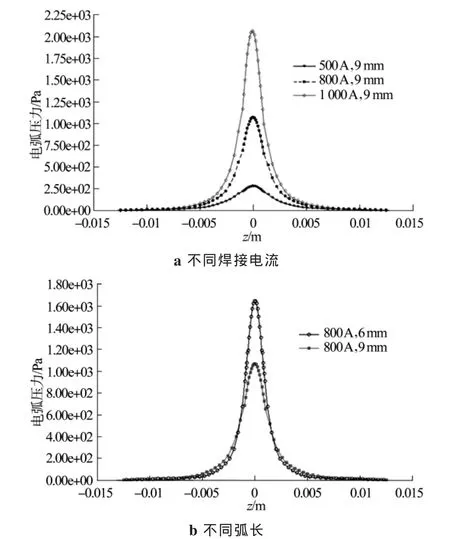
图12 工件上表面的电弧压力分布Fig.12 The calculated results of the arc pressure on weldment surface
(1)以K-TIG焊枪为研究对象,根据磁流体动力学理论构建了计算模型,该模型包括焊枪内部保护气体流动区域和电弧区。
(2)利用FLUENT软件,采用有限元数值模拟方法,考虑紊流,得到了焊接电流为500 A、800 A、1000 A时的温度分布、电势分布,压力分布及等离子体速度场分布状态,反映了K-TIG焊接电弧的特性。
(3)大电流形成的较大电弧压力是小孔形成的关键因素。
[1]Lathabai S,Jarvis B L,Barton K J.Comparison of keyhole and conventional gas tungsten arc welds in commercially pure titanium[J].Materials Science and Engineering,2001(A299):81-93.
[2]Jarvis B L,Ahmed N U.Development of keyhole mode gas tungsten arc welding process[J].Science and Technology of Welding and Joining,2000,5(1):1-7.
[3]Lathabai S,Jarvis B L,Barton K J.Keyhole gas tungsten arc welding of commercially pure zirconiu m[J].Science and Technology of Welding and Joining,2008,6(13):573-581.
[4]Lathabai S,Jarvis B L.Keyhole gas tungsten arc welding of Titanium and Titanium Alloys[D].USA:Corrosion Solution Conference,Coeur d'Alene,2003.
[5]殷凤良,胡绳荪,郑振太.等离子弧焊电弧的数值模拟[J].焊接学报,2006,27(8):51-54.
[6]武传松.焊接热过程数值分析[M].黑龙江:哈尔滨工业大学出版社,1990.
[7]Ohring S,Lugt H J.Numerical simulation of a time-dependent 3-D GTAW weld pool due to a moving arc[J].Welding Research Supplement,1999(12):416-424.
[8]CHOO R TC,SZEKELY J,WESTHOFF R C.On the Calculation of the Free Surface Temperature of Gas-Tungsten-Arc Weld Pools from First Principles:Part Modeling the Welding Arc[J].Metallurgical Transactions B,1992,6(23):357-369.
