拉剪组合状态下的锚杆极限承载力分析:基于BP神经网络

李 颖，王华福

(1.浙江水利水电专科学校，浙江杭州 310018;2.中国水电顾问集团华东勘测设计研究院，浙江杭州 310014)

神经网络是在物理机制上模拟大脑信息处理机制的非线性信息系统，由大规模并行连接而成的神经元组成.与现有的数值计算和符号计算原理不同，神经网络具有处理信息的思维、学习和计算功能.BP网络是目前应用得最广泛的一种神经网络，它具有多层前馈网络结构.神经网络产生于20世纪40年代，由于计算机技术的进步，并于20世纪80年代得到飞速的发展，在许多领域得到应用.近20年来，人工神经网络在土木工程领域被大量应用，处理各种非线性问题，如路基材料性状预测［1］、混凝土优化配合比设计［2］、本构模型分析［3］、钢筋混凝泥土柱侧向承载力［4］等.

一般锚杆极限承载力通过锚杆静荷载—位移曲线来确定，该方法操作简便，结果直观可信，在工程上得到广泛应用.但是由于承载力影响因素的众多，变量之间的关系复杂，很难用确切的数学模型来描述，单次试验代表性不明确.另外，试验时间长，对结构具有破坏性，从一定程度上影响力具体工程的准确评估.传统的梁板植筋加固中锚杆受拉剪组合荷载作用而处于复杂的应力状态，其极限承载力的预测一直是建筑结构加固设计中的难点问题.本文基于BP神经网络，提出了拉剪组合状态下锚杆极限承载力预测方法，算例表明该方法具有较高的精度，并通过参数分析对具体影响因素进行了深入探讨.

1 BP神经网络结构模型

1.1 样本选取和预处理

训练样本的选择对网络的训练十分重要，本文中的样本来自何勇［5］，刘新红［6］及本文作者实测数据，共66个样本，其中5个样本的数据为后面要用到的验证样本.

前期试验研究分析表明，拉剪组合荷载作用下锚杆极限承载力受诸多因素的影响，主要包括锚杆及混凝土的力学特性、锚固及加载方式、锚杆的直径及植入深度等.本文通过模型试验和资料分析，选取混凝土抗压强度、锚杆钢筋屈服强度、无机胶粘结强度、锚杆的直径、植入深度和加载角，即锚杆中轴线与荷载方向的夹角作为主要输入变量，构建BP经网络结构模型;输出变量为各种拉剪组合荷载作用下锚杆的极限承载力.

典型的BP神经网络包括输入层、隐含层和输出层，同层单元之间不连接，具体的网络结构模型见图1.输入层含有6个输入神经元，隐含层含有8个神经元，输出层含有1个神经元及极限承载力.输入层变量取值范围如下:混凝土抗压强度x1:20～50 MPa;锚杆钢筋的屈服强度x2:300～400 MPa;无机胶的粘结强度x3:5～20 MPa;锚杆直径x4:16～25 mm;锚杆植入深度x5:110～450 mm;试验加载角x6:0～π/2.

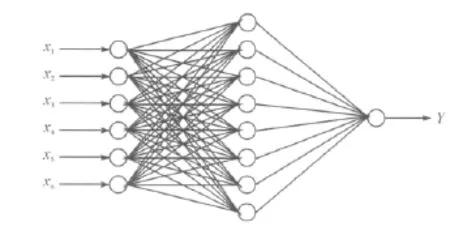
图1 BP神经网络模型结构

1.2 算法的选择与初始参数设置

BP算法的学习过程一般包括正向传播和反向传播两部分.正向传播指输入模式从输入层经隐含层逐层处理，最终传给输出层，每一层神经元的状态仅对下一层神经元的状态造成影响.如果输出结果与期望值相比，误差较大，则实施反向传播，将误差信号原路返回，通过修改神经元的权值，减小误差.

MATLAB具有强大的数值计算功能、符号运算功能和图形处理功能.本文选取MATLAB作为预测算法实施平台，直接调用其内部函数作为BP神经网络的传递函数及训练函数.隐含层传递函数选为tansig函数，输出层传递函数选为purelin函数，网络训练函数则为traindm函数.traindm函数在训练中采用了有动量的梯度下降法，该方法降低了网络对于误差曲面局部细节的敏感性，减少了学习过程的振荡趋势，从而改善了训练过程的收敛性，提高了学习速度并保证了算法的相对可靠性.

主要训练参数设置如下:样本训练次数 net.trainparam.epochs=5000;网络性能误差目标 net.trainparam.goal=0.001;显示间隔数 net.trainparam.show=50;学习效率 net.trainparam.ir=0.05;其他训练参数设为缺省值.

BP神经网络训练过程误差变化曲线见图2，结果表明收敛性较好，络训练到2 295步时误差就能达到目标值0.001.

图2 网络训练的误差变化

2 BP神经网络应用

2.1 锚杆极限承载力预测

为了检验本文构建的BP神经网络的有效性，对5个验证样本的锚杆极限承载力进行了预测.神经网络预测结果与模型试验结果的比较见表1.

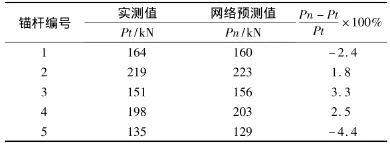
表1 预测结果与试验结果的对比

由表1可以看出，预测结果与试验结果的误差在5%的范围内.因此，本文建立的神经网络结构模型具有较高的精度，可以被应用于锚杆的极限承载力的预测.

2.2 影响因素分析

采用训练成熟的BP神经网络，对拉剪组合荷载作用下的的锚杆极限承载力影响因素进行分析，以便更好地服务于工程设计.

锚杆直径对极限承载力的影响如图3所示.选用钢筋植入深度;混凝土抗压强度;锚杆钢筋的屈服强度;无机胶的粘结强度.分析表明，锚杆的直径对极限承载力的影响显著，随着锚杆直径的增加，极限承载力增大;锚杆在拉剪组合荷载作用下的极限承载力预测值较椭圆拟合分析值要大，这与模型试验结果一致［5］.

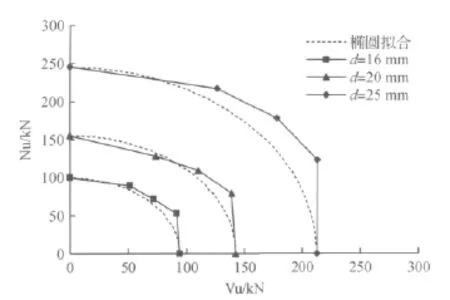
图3 锚杆直径对锚杆极限承载力的影响

锚杆植入深度对极限承载力的影响如图4所示.选用锚杆直径;混凝土抗压强度;钢筋屈服强度;无机胶粘结强度.分析表明，随着钢筋植入深度的增加，锚杆的极限承载力增大;然而当植入深度超过时，极限承载力增长幅值显著降低，这也说明植筋锚杆存在一个有效植入深度.同样，锚杆在拉剪组合荷载作用下的极限承载力预测值较椭圆拟合分析值要大，这与模型试验结果一致［8］.

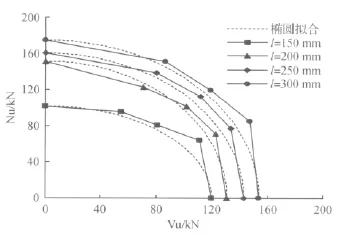
图4 植入深度对锚杆极限承载力的影响

3 结语

本文运用BP神经网络方法对拉剪组合荷载作用下梁板植筋加固中锚杆的极限承载力进行了预测.通过神经网络预测值与模型试验实验结果的比较分析表明，该方法具有较高的精度，可以应用于工程实践.在此基础上利用训练好的神经网络，进行指定的输入与输出，对拉剪组合荷载作用下锚杆极限承载力的影响因素进行了深入探讨.

BP神经网络原则上可以实现任意线性和非线性的函数映射，但由于BP神经网络是基于动量梯度下降的误差反向传播算法进行学习的，所以其网络训练效率较低，容易陷入局部极小值点，尽管目前采用一些改进的快速学习算法可以较好地解决某类具体问题，但在设计过程中一般要经过反复地试凑和训练过程.因此，为了更好地对实际工程中锚杆承载力形状进行分析，需要建立更为复杂神经网络拓扑结构和预测模型.

［1］李永靖，王 强，高 平.基于改进BP神经网络的路基材料性能预测［J］.辽宁工程技术大学学报，2004，23(1):57-58.

［2］杨天才，刘 鸿，程绍佳，等.一种神经网络模型在混凝土配比设计中的应用［J］.武汉工程职业技术学院学报，2003，15(2):21-23.

［3］魏 星，黄茂松，虎旭林.采用神经网络材料本构模型的智能有限元及其算法［J］.宁夏大学学报，2002，23(3):237-240.

［4］焦俊婷，于霖冲，叶英华，等.基于人工神经网络的压弯钢筋混泥土柱侧向承载力的预测［J］.工业建筑，2006，36(1):27-29.

［5］何 勇.混凝土结构化学粘结锚杆锚固性能的研究［D］.武汉:武汉大学，2001.

［6］刘新红.自锁锚杆抗剪性能试验研究［D］.武汉:武汉大学，2003.

［7］李 颖.在拉剪组合荷载组合作用下自锁锚杆锚固性能试验研究［D］.武汉:武汉大学，2004.