多节点加载预应力锚索格构梁室内模型试验研究

2012-08-02刘晶晶赵其华张文居彭盛恩

水土保持研究 2012年2期

刘晶晶，赵其华，张文居，3，彭盛恩，周勇，于宇

（1.核工业西南勘察设计研究院有限公司，成都610061；2.成都理工大学地质灾害防治与地质环境保护国家重点实验室，成都610059；3.四川广甘高速公路有限责任公司，成都610041）

在预应力锚索格构梁的力学计算模型中，主要研究的是锚索格梁与其下岩土体（即地基）的相互作用，因此，预应力锚索格梁的力学模型主要由其下岩土体的地基模型所决定。目前计算格构梁的力学模型中，对格构梁和周围岩土的作用多采用弹性地基梁法进行计算，在弹性地基梁模型中，将格构梁视为地基上的梁。不同的弹性地基梁模型，主要区别在于地基模型的选取不同。对于边坡上的格构梁，受坡角和锚索倾角的影响，梁底面摩擦力的存在使得格构梁受力变得复杂，此时选取正确的、合理的地基模型便显得尤为重要。本文在前期的单节点加载预应力锚索格构梁模型试验[1]的基础上进行了多节点加载模型试验研究，并与理论计算进行对比分析，找出更为符合实际、适合工程应用的格构梁计算方法。

1 多节点加载模型试验

1.1 模型格构梁的选用

本次试验模型格构梁纵梁、横梁截面尺寸均选用1.6m×60mm×80mm，跨距600mm，悬臂长200 mm（见图1），模型材料的选取、制作过程及其与原型的相似性等参见文献[1－2]，此处不做过多阐述，模型横剖面见图2。

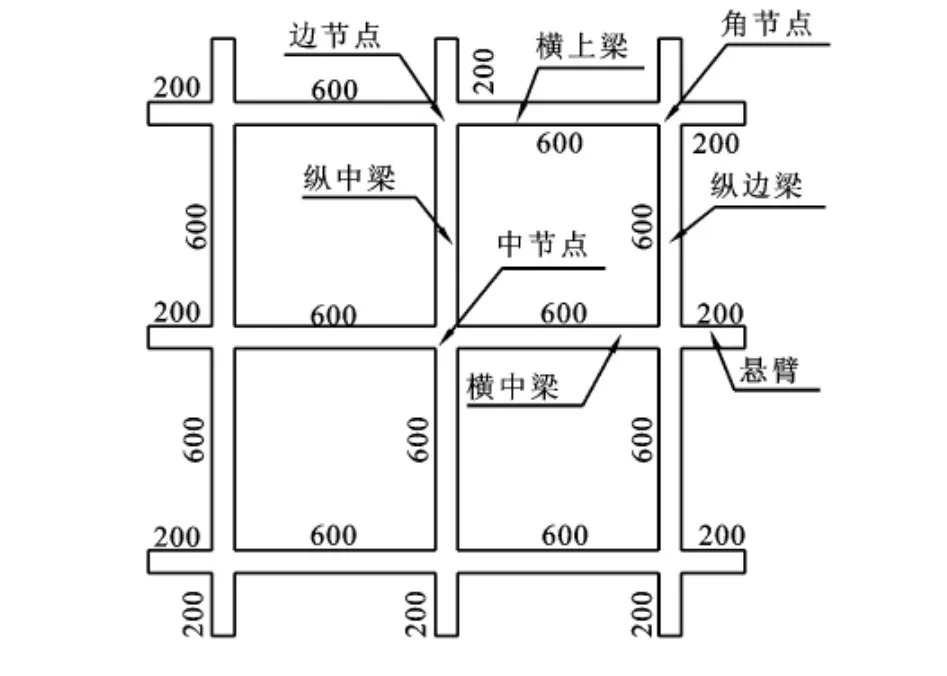
图1 模型格构梁示意图（单位：mm）

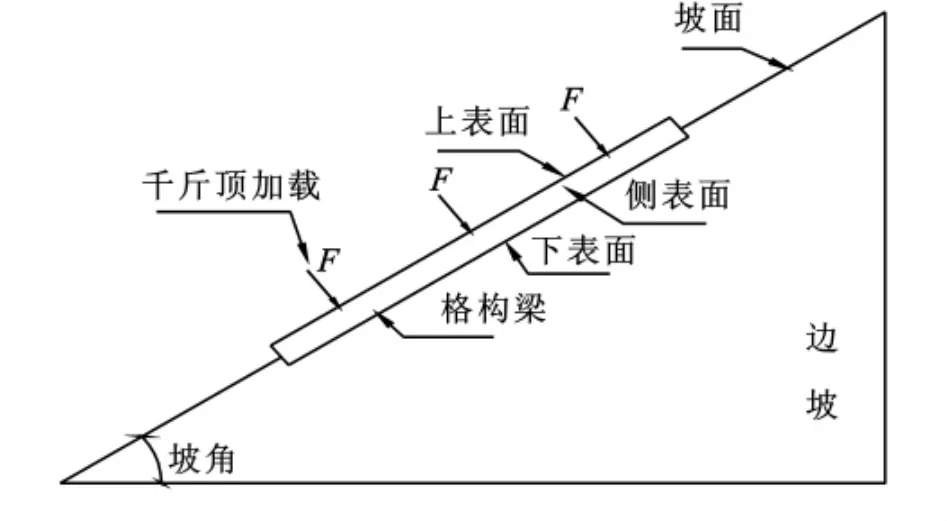
图2 模型横剖面示意图

1.2 应变片的布置

格构梁上、下表面沿着梁跨的方向将应变片粘贴在中轴线上，可测得上下表面的拉、压应变；侧表面应变片的粘贴与中轴线成45°，用来测量由扭矩引起的剪应变，通过测得的应变来计算格梁弯矩及剪力。根据所要研究的具体内容以及加载方式，在格构梁右上角1／4框架内布置应变片，具体布置如图3所示。

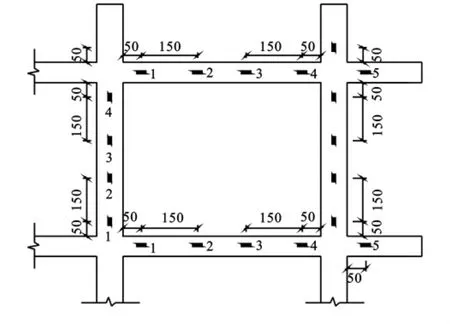
图3 应变片布置图

1.3 加载方式

本次试验采用多节点加载模型格构梁来模拟实际工程中的预应力锚索格构梁，预应力方向与坡面法向的夹角为25°，以模拟锚索倾角，分两级加载，各级加载荷载值为0.1MPa。

1.4 测试结果分析

由于横梁摩擦力沿梁宽方向分布，因此摩擦力对其内力影响较小，因此，本节只对纵梁测试结果进行分析。根据测试结果计算出来的纵梁弯矩、剪力见表1。

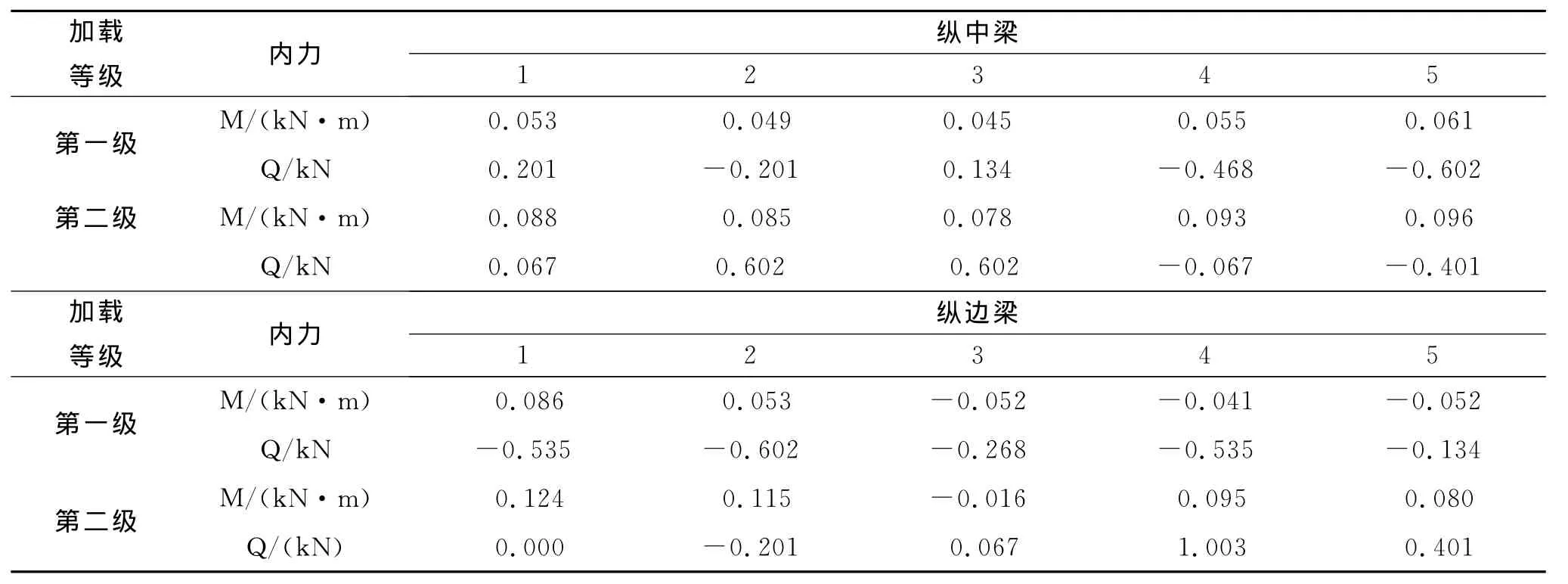
表1 格构梁内力计算结果

从表1中的数值可以看出，纵梁弯矩在跨中处以及荷载作用处较大，随着外荷载值的增大，在跨中处很有可能出现最大负弯矩，由此可以推测格梁的危险截面有可能是在跨中或加载节点处；格构梁跨中和悬臂处剪力较大，在实际工程中进行配筋时在此两处可适当增大箍筋间距。

2 理论计算方法

2.1 主要的地基模型

弹性地基梁主要的地基模型有以下几种[3]：文克尔地基模型、利夫金模型、弹性半无限地基模型、有限压缩层地基模型、双参数地基模型、非线性模型等，这些模型大多与实际地基条件出入较大，存在很多不确定因素，计算繁琐，并不适合工程设计人员实际运用。

2.2 考虑摩擦的Winkler弹性地基梁法

Winkler地基模型实质上是将地基看作无数分割开的小土柱，表现为一根根弹簧组成的一系列各自独立的弹簧体系。然而，当存在水平作用力时，地基梁可能由受弯状态转变为偏心受压状态，对地基梁的配筋设计影响很大。尤其是当地基比较坚硬且地基与梁的接触较为粗糙时，地基与梁之间的水平摩阻力的存在是明显的，此时就有必要考虑地基与梁之间的水平摩阻力的影响。

2.2.1 微分方程的建立考虑摩擦的Winkler地基被视为具有竖向和水平反力的弹性支撑体，地基的竖向反力仍采用Winkler地基假设，即竖向反力与该点的沉陷成正比[4－5]，水平反力假设与梁底同地基之间的相对水平位移成正比，即地基的竖向反力qv和水平反力qu可表示为：

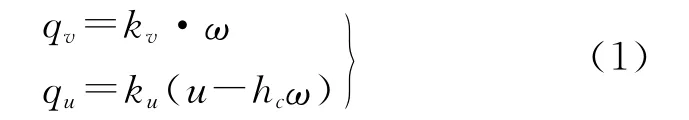
式中：kv，ku——地基竖向和水平向的反应模量，通过对模型坡体进行压缩试验测定；w，u——梁的挠度和截面水平位移；hc——梁中性轴到梁底的距离。

从dx一段梁的外力平衡条件，可得到梁的内力——弯矩M、剪力Q、轴向力N的关系式：

由方程（2）消去梁的内力，得到如下微分方程组：

式中，E，I和A分别为梁的弹性模量（通过混凝土应力应变曲线试验测定）、惯性矩和截面面积。

2.2.2 计算结果现针对本次模型试验，考虑摩擦力对格梁的纵梁影响（横梁受摩擦力影响较小，故不予考虑），理论计算在多节点加载条件下纵梁的最大挠度ωm、最大弯矩Mm、最大轴向力Nm和地基最大摩阻应力Zm，计算结果见表2。

表2 ωm，Mm，Nm和Zm计算结果

从表2中可以明显看出纵边梁的变形和内力计算结果明显大于纵中梁，其中纵边梁的最大挠度ωm和最大弯矩要大于纵中梁27%～28%，而最大轴力和最大摩阻应力的差值则达到了74%和88%，产生该差异的原因是由于纵边梁只受到左侧三根横梁的制约，而右侧的悬臂由于长度较小，其对纵边梁变形的约束完全可以忽略，而纵中梁左右均受到横梁的制约，因此变形较边梁小，由此亦可以看出在实际工程中整片格梁在坡脚、坡顶以及两侧边界处的边梁其变形及内力都要远远大于中间部分的格梁，在进行格梁内力计算时要分开考虑。

分析最大摩阻应力计算结果可以看出，当将其换算成总的摩擦力时，该值较大，且由于纵边梁和纵中梁在最大摩阻应力上的差异达到了88%，比在挠度和弯矩上的差异大了3倍多，因此说明平行坡面的摩擦力对不同位置处的格梁变形的影响较大，因此在实际计算时不可忽略。

3 试验结果与理论计算的对比分析

通过上述分析，可知纵梁受摩擦力影响较大，现对纵梁的最大弯矩进行对比分析，纵中梁、纵边梁根据实测结果计算的最大弯矩与理论计算最大弯矩见表3。

表3 纵中梁、纵边梁最大弯矩对比 kN·mm

从表3中可以看出，实测最大弯矩同理论计算值总体上相差不大，说明考虑摩擦的Winkler地基梁计算方法较为合理，但理论计算值要略小于实测值，分析其原因是由于锚索作用力的相互叠加效应，使得纵中梁和纵边梁的弯矩值较理论计算值大出3.7%和7.7%，此外从该数值上可以看出纵边梁的差距要比纵中梁大出一倍左右，由此可以看出边梁的内力以及变形受外界条件影响较大，因此在进行格梁设计计算时要充分考虑到此点。