一类含毒素功能性反应的捕食系统动力学分析

朱慧颖，沈莉莉，赵维锐

(武汉理工大学理学院，湖北 武汉 430070)

自20世纪80年代以来，不少学者开始对毒素在植物－食草动物系统的作用以及毒素对个体生长模型的影响进行研究。但遗憾的是这些模型中都没有涉及到对时滞的讨论。为了能够更好地研究动植物系统的动力学行为，笔者在充分考虑消耗的植物量转换成新的动物量的时间滞后性的前提下，构造了新的植物－食草动物模型，并分析了该系统的一系列动力学性态。

1 模型建立

为了刻画植物毒素对食草动物的影响，冯芷兰等在传统的Holling－II型[1－3]功能性反应中加入了毒素对食草动物成长影响的功能性反应:

则原来的植物－食草动物系统变为:

其中:r为植物的内禀增长率;K为环境容纳率;B为被消耗的植物量转换成新的动物量的转换率(食草动物通过对植物的觅食获得增长和繁殖);d为食草动物的死亡率，该死亡率与植物毒素无关;G=M/(4T);M为单位时间内食草动物能忍受的最大毒素量;T为单位植物所含的毒素量。因此，G的值越小，食草动物受到毒素的影响就越大。

同时式(1)和式(2)的建立基于这样一个假设:食草动物在吞食植物后，立刻获得增长和繁殖。这显然是不符合实际的，在现实中食草动物通过觅食实现增长和繁殖是需要一定时间的。为了分析这一段时间对系统稳定性[4]的影响，引进滞量τ，对原系统做如下改变:

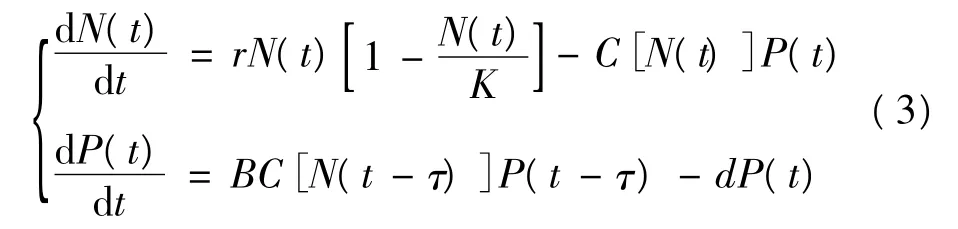
式(3)假设食草动物能控制自己的消化率，当植物密度足够大时，食草动物就会减少对植物的消化量。故设定一个阈值Nm:当植物量N不高于阈值Nm时，食草动物的消化率为常数;当植物量N超过阈值Nm时，食草动物的消化率就是植物量N的递减函数。

对于这种情况，可以假设:

式中，σ0＞0为一个常量。σ是N的函数，为食草动物的消化率。在对σ(N)做了如上假设之后，C(N)也发生了变化，故不妨假设:

为了便于讨论，引进记号g1(N)，令:

则可将式(3)改写成:

2 系统的一致持久性

为证明主要定理，先引进如下引理:

引理1系统满足初值条件:N(t)=φ1(t)＞0，P(t)=φ2(t) ＞0，t∈[－τ，0]的所有解在 t＞0上均为正。

证明首先证明N(t)在t＞0上大于零。由式(7) 可得:。e为食草动物的觅食率，其大小取决于捕食者即食草动物的移动速度以及其能侦测到的食饵的分布区域的半径大小。由于φ1(0)＞0，显然当t＞0时，N(t)恒为正。

下面证明P(t)在t＞0上大于零。假设存在t∈(0，+∞)，使得 P(t) ＜0。由于在[－ τ，0]上P(t)=φ2(t)＞0，因此0，显然P'(t1)≤0。由式(7)知:

则N(t1－τ) ＞0，P(t1－τ) ＞0，从而 P'(t1) ＞0与P'(t1)≤0矛盾。因此当t∈(0，+∞)，P(t) ＞0。

引理2式(7)在总是点耗散的。

证明由式(7)的第1式知:，由于方程满足初始值为u(0)=u0的解为则由比较定理知:于是

下面证明存在M2＞0，使得P(t)≤M2。

令 W(t)=BN(t)+P(t+τ)，由式(7)可得:

进一步引进如下引理:

考虑一个度量为d的度量空间X，T为X上的一个连续半流，即:T0(x)=x，x∈X;Tt+s=TtTs，t，s≥0。Tt(x)关于 t和 x连续，集合X中的点 x到集合X的子集Y的距离记作记过x的正半轨线极限集为B是紧的不变集，定义WS(B)为B的稳定集:;将定义为

假设1假设X为开集X0的闭包，∂X0为X0的非空边界。T(t)为定义在X上的半群满足:T(t):X0→X0，T(t):∂X0→∂X0。

引理3若T(t)符合假设1且满足:

(1)存在t0≥0，使得T(t)在t＞t0时是紧的;

(2)T(t)在X上是点耗散的;

则T(t)是一致持久的，当且仅当每一个Mi∈M 时，WS(Mi)∩X0=φ。

该引理的证明见文献[5－6]。

关于式(7)的持久性，有如下结果:

定理1式(7)是一致持久的，如果a0＞d，其中h 为捕食者对每一份食饵的掌控时间，即食草动物消化每一份食物所需要的时间。

证明由引理2可知，存在K1＞0，K2＞0，使得式(7)的所有解[N(t)，P(t)]均满足:0≤N(t)≤K1，0≤P(t)≤K2，从而系统相空间 X 是一个定义在[－ τ，0]上，取值在[0，K1]×[0，K2]的正锥，记为 C[[－ τ，0]，K1]× C[[－ τ，0]，K2]。再由引理1知:正锥X是一个不变集。对于任意一对初始函数(φ，φ)∈X，令 X(t，φ，φ)为式(7)的解，并记 T(t)(φ，φ)(θ)=[N(t+ θ，φ，φ)，P(t+θ，φ，φ)]，－ τ≤ θ≤0，T(t):X →X，则满足:首先 T(t)是连续的，其次对于N(t)≤M1，P(t)≤M2，都有故 T(t)在t≥τ上是全连续的，从而T(t)在t≥τ上是紧的。因此引理3的条件(1)满足，又由引理2可知条件(2)也是满足的。

定义 C+([－ τ，0]，R2+)为所有[－ τ，0]上的非负连续函数的集合，并记:

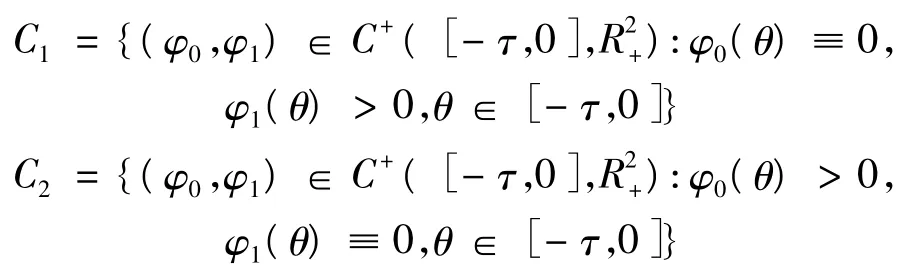
记 C=C1∪C2，X=C+([－ τ，0]，R2+)，X0=intC+([－ τ，0]，R2+)，则 C= ∂X0，故式(7)有两个常数解E0，EK:

以下证明 WS(Ei)∩X0=φ，i=0，K。

先证WS(E0)∩X0=φ。假设WS(E0)∩X0≠φ，即存在 N(t) ＞0，P(t) ＞0，使得limt→∞[N(t)，P(t)]=(0，0)。由式(7)的第一个方程可以得到:

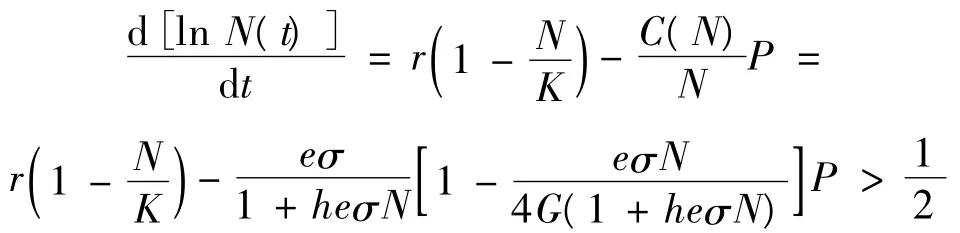
接着证明 WS(EK)∩X0=φ。同样假设WS(EK)∩X0≠φ，即存在 N(t) ＞0，P(t) ＞0，使得，则对任意小的正数 ε:

使得N(t)＞K－ε，P(t)＜ε。其中a0=B·故由式(7)可得:存在T=T(ε)，使得:

考虑系统:

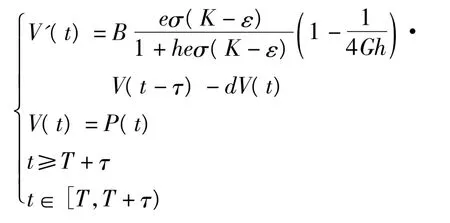
综上所述，式(7)满足引理3的所有条件，则式(7)是一致持久的。

3 正平衡点的全局吸引性

假设τ=0，即考虑不含时滞的系统，则:

定义1如果式(9)的任意一个正解[N(t)，P(t)]满足:则称式(9)的正平衡点(N*，P*)是全局吸引的

。

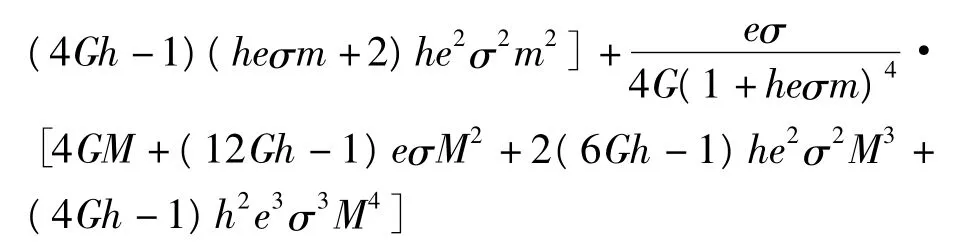
定理2如果 r/K＞I1，a0＞d＞I2，则式(9)的正平衡点(N*，P*)是全局吸引[8]的。

证明设[N1(t)，P1(t)]是式(9)的任意一个正解，则由引理2可知，存在 t*，M≥m＞0，使得当t＞t*时，有 m≤Ni(t)≤M，m≤Pi(t)≤M，i=1，2。 定 义 Lyapunov 函 数 V(t) =沿着式(7)的解计算V(t)的Dini导数:

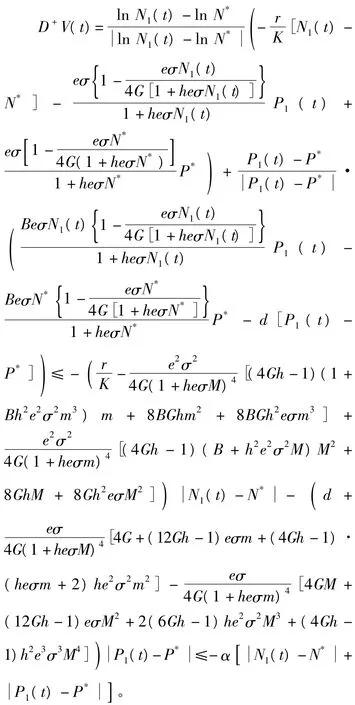
其中，α=min{I1，I2}，对上述不等式两端从

t*到t进行积分，可得:

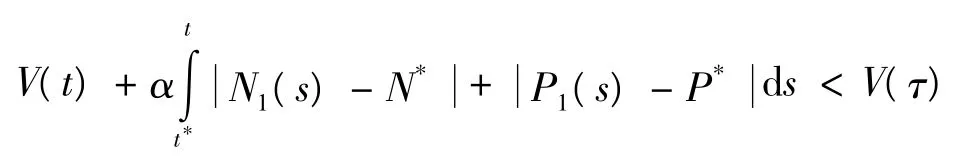
因此，当t＞t*时有:

故式(9)的正平衡点是全局吸引的。

4 结论

通过在模型中引入消耗的植物量转换成新的动物量的时滞，对系统的一致持久性、平衡点的全局吸引性进行了讨论，由定理1知，当a0＞d时，这里，式(7)是一致持久的。这表明食饵量达到顶峰状态时，捕食者的出生率大于其死亡率是捕食者和食饵一致持续共存的充分条件。

[1] HOLLING C S.Some characteristics of predation and parasitism[J].Can Ent，1959(91):293 － 320.

[2] LI Y，FENG Z，SWIHART R，et al.Modeling plant toxicity on plant herbivore dynamics[J].J Dynam Differential Equations，2006，18(4):1021 －1024.

[3] LIU R，FENG Z，ZHU H.Bifurcation analysis of a plantherbivore model with toxin－determined functional response[J].J Differential Equations，2008，20(5):442－467.

[4] 沈莉莉，赵维锐.一类具有时滞和带毒素功能性反应的植物－食草动物性态分析[J].湖北民族学院学报:自然科学版，2010，28(1):41 －45.

[5] HALE J K.，WALTMAN P.Persistence in infinite － dimensional systems[J].Society for Industrial and Applied Mathematics，1989(20):388 －395.

[6] LIU R，FENG Z，DONALD L D.Plant－ herbivore interactions mediated by plant toxicity[J].Theoretical Population Biology，2008(73):449 －459.

[7] HARA T，SUGIE J.Stability region for systems of differential－ difference equations[J].Funk Ekvac，1996(39):69－86.

[8] WANG K，WANG W，LIU X.Global stability in a viral infection model with lytic and nonlytic immune response[J].Comput Math Appl，2006(51):1593－1610.