一种改进的基于训练符号的 OFDM 同步算法

林 云，张红帅，刘向玉

(重庆邮电大学移动通信重点实验室，重庆400065)

0 引言

正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)因具有较高的抗干扰能力和频谱利用率，越来越受到人们的关注。但是OFDM系统对符号定时和频率偏移问题非常敏感，错误的符号定时将会导致很高的符号间干扰(Inter-symbol Interference，ISI);而频率偏移则会导致载波间干扰(Inter-carrier Interference，ICD)，如果不采取措施对这种ICI加以克服，会给系统带来严重的“地板效应”。在 Schmidl及 Cox算法［1］中，Schmidl提出了基于训练符号的时频联合同步算法。该算法使用了2个训练符号，第1个训练符号用于符定时同步以及小数倍频偏的估计;第2个符号利用和第一个符号的差分关系来完成整数倍频偏估计。但是由于循环前缀(Cyclic Prefix，CP)的存在，在进行符号定时时会出现一个“平台”区，使符号定时不准确。

1 同步信号的产生

图1给出了0FDM系统的发射链路工作原理。发送端将被传输的信号转换成子载波幅度及相位的映射，并进行傅里叶反变换(IFFT)，将数据的频谱表达式变换到时域上。发送端的操作与接收端相反，将射频(Radio Frequency，RF)信号与基带信号进行混频处理，并用FFT变换分解频域信号，子载波的幅度和相位被采集出来并转换回数字信号。FFT和IFFT互为反变换，选择适当的变换将信号接收或发射。由于FFT操作类似IFFT，因此发射机和接收机可以使用同一硬件设备。

图1 OFDM的发射端框图

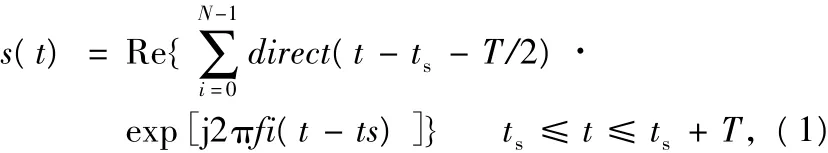
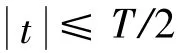
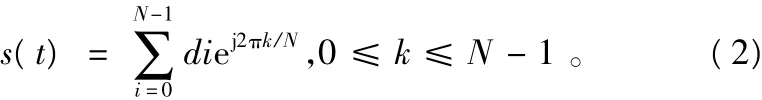
将得到的s(t)经过变频后得到射频信号，经发射天线发射出去，这就是OFDM发射机的工作原理。系统接收端的工作原理是发射端工作原理的逆操作，并通过跟踪和捕获，来完成系统的符号同步及载波频率同步。

2 符号定时和频率同步方案

2.1 符号定时

Schmidl＆Cox算法是基于2个长度都为N的训练符号的定时和频率偏移联合估计。其第1个训练符号是完全对应相等的2部分，接收端就是利用这一特点来完成数据的相关，从而完成符号定时同步和小数倍频偏估计的，但是由于CP的存在，使得该算法产生一个峰值平台，这就造成符号定时不准确。Minn算法［2］和 Park算法［3］中分别提出了新的训练符号结构，虽然都能消除Schmidl＆Cox算法中的峰值平台，但是在低信噪比的情况下，伴生的旁瓣可能和定时函数值相等，从而使定时仍然不够准确。而由于循环前缀往往包含的采样点比较少，如果单单利用循环前缀来做符号定时的时候容易受到噪声的影响。图2是这3种算法训练结构的比较。

图2 3种算法的训练符号结构图

其中，－A是A的取反，B是A的倒序，B*是B的共轭。以上几种算法的都各自有优缺点，这里利用循环前缀的特性，在Schmidl算法的基础上利用双滑动窗口得出了一种改进的基于循环前缀和训练符号的定时、频偏联合估计算法。为了方便可以假设该训练序列中有N个采样点，平均分成2份，最后N/8个采样点复制到序列的前面作为循环前缀。第1个滑动窗口的长度为N/8。则该滑动窗口对应的符号比特r(n)，与其相隔N个采样点长度的比特共轭相乘，累加:

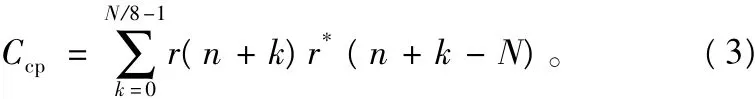
对Ccp进行能量归一化为:

粗定时频偏估计函数为:

当Mcp取得最大值时所对应的采样点就是所要找的初始定时位置。之后再让训练序列经过一个长度为N/2滑动窗口，该滑动窗口对应的数据比特r(n)，与其相隔N/2个采样点的数据比特共轭相乘，累加。

对其进行能量归一化:

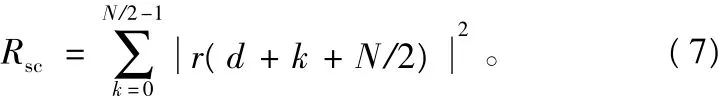
如图3所示，为这里算法的符号同步判决函数的仿真特性，仿真参数为:载波数目N=256，循环前缀的长度32，SNR=20 dB，信道为AWGN信道。

细定时同步函数为:

图3 基于循环前缀的符号定时

由于循环前缀和训练符号最后N/8完全相等，所以相关性非常强，当它们一一对应做相关时，Mcp取得最大值，但是在低信噪比的情况下容易受到噪声的影响，所以只能用来做粗定时。如图3所示新算法准确的定时位置为2条曲线的交点所对应的采样点。

2.2 频率偏移估计

频偏估计在OFDM中占有比较大的位置，因为频率偏移比较严重的时是OFDM子载波的正交性遭到破坏，这对OFDM系统来说是致命的，所以对频率偏移的研究就显得特别重要，最近几年也取得了一些成就，如参考文献［4－6］的算法。这里算法中第1个训练符号在时域上是完全相等的2部分，因此可以表示为:

经过AWGN信道后，接受信号变为:

式中，ε为频率偏移，W(n)为噪声。

当忽略噪声时:r(n+N/2)=r(n)ejπε，可以很清楚地看到，训练符号的第1部分和第2部分存在一个固定的相位差φ=επ，现在就可以利用这个相位差来做频率偏移估计。如果相位差φ∈－π，[]π，则数据只存在小数倍频率偏移，可以利用Schmidl算法中的方法来求出:

如果φ ∉ [ －2π，2π ]，则除了小数倍偏移，还存在整数倍频率偏移，总的频偏为:

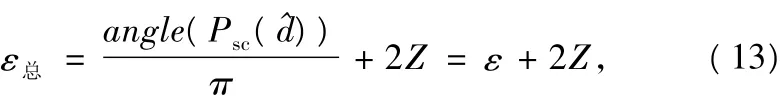
式中，Z为整数倍频偏。在补偿完小数倍频率偏移之后，把时域信号经过FFT变换为频域信号，再利用参考文献［1］中第1个训练符号和第2个训练符号之间存在的差分关系来求出Z。

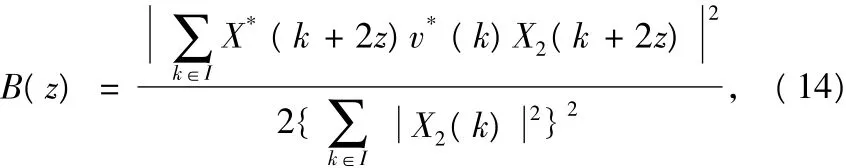
式中，I为偶频率分量的下表集，把B(z)最大时的z作为频率的估计值，当估计出z后就可以得到SC算法的总的频率偏移ε总。

3 仿真结果

在仿真中，OFDM系统的主要参数为:子载波数N=256，循环前缀CP的长度为32个采样点，256点的IFFT/FFT，频偏归一化为10。采用6条多径，各个信道的时延用采样的样点数来表示。具体多径参数设计如下:路径1，2，3，4，5，6 分别延迟 0，3，6，9，12，15，各信道增益分别为0 dB，－2 dB，－4 dB，－6 dB，－8 dB，－10 dB。分别在 AWGN和多径信道中，对1 000个符号进行仿真。

采用均方误差(MSE)来衡量定时算法的性能。从图4和图5可以看出，不管是在高斯信道还是多径信道中，新算法得到的符号定时估计的MSE都近似为0，Schmidl算法在信噪比(SNR)小于5 dB时定时估计的MSE都比较大，虽然SNR＞5 dB后误差明显减少，但仍然相比新算法较大。

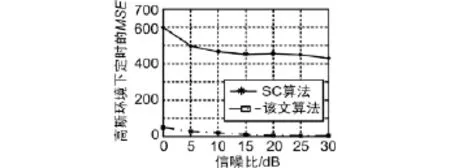
图4 AWGN信道下符号定时估计的MSE

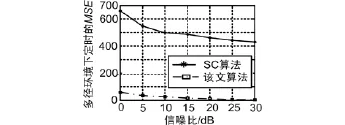
图5 多径信道下符号定时估计的MSE

归一化频率偏移的均方误差(MSE)用来衡量频偏估计算法的性能。由于新算法是在Schmidl算法训练符号的基础上做的频率偏移估计，从图6和图7可以看出不论在高斯信道还是多径信道中这里提出的频偏估计算法和参考文献［1］中算法的性能相当，都在系统允许的精度范围内。

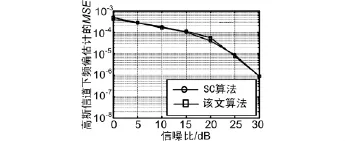
图6 AWGN信道下频偏估计的MSE

图7 多径信道下频偏估计的MSE

4 结束语

在OFDM通信系统中，同步起着至关重要的作用。符号定时不准确，后面的IFFT解调将找不到准确的开始位置，同时给系统带来较大的ISI。小数倍的载波频率偏移会使子载波的正交性遭到破坏，影响系统性能，而整数倍的载波载波频率偏移如果不纠正的话，会使解调数据出现50%的误码率。文中在Schmidl算法的基础上做出了改进，新算法克服了它的缺点，能够实现准确的定时和频率偏移同步。

［1］SCHMIDLT M，COX D C.Robust frequeney and timing synchronization for OFDM system ［J］.IEEE Trans.Commun，1997，45：1613 －1621.

［2］MINNH，ZENG M，BHARGAVA V K.On timing offset estimation for OFDM system［J］.IEEE Commun.Left，M.2000(7)：242 －244.

［3］BYUNGJOON P.A Novel Timing Estimation Method for OFDM systems［J］. IEEE COMMUNICATIONS LETTERS，2003，7(5)：269 －272.

［4］廖腾达，谢显中，郑平莲.基于循环前缀的LTE系统多普勒频偏估计算法［J］.电视技术，2010，34(1)：56 －58.

［5］LAMBRETTE U，SPETH M，MEYR H.OFDM burst frequency synchronization by single carrier training data［J］.IEEE Communication.Letters，1997(9)：46 －48.

［6］方绍，谢显中.基于DVB－T的OFDM频偏估计算法及 DSP 实现［J］.电视技术，2011，33(3)：5 －8.