物流配送网络节点服务客户饱和度模型构建

张 旭 凤

（1.北京工业大学，北京市 100124；2.北京物资学院，北京市 101149）

一、引 言

随着经济的发展，产品的流通范围越来越大，链条越来越长，物流企业为了更好地为货主企业开展物流服务，需要不断扩大自己的物流配送网络。在物流配送网络的生成和运作过程中，特别是随着服务客户数量的增加，物流配送节点所提供的服务无法满足客户的要求，在这种情况下，意味着目前的节点已经达到了服务极限。在物流企业的实际运作过程中，一般会增加新的节点以满足客户要求，即建立新的配送中心。由此可见，在物流配送网络的扩展过程中，对于基于客户服务水平的物流配送节点饱和值的研究是非常重要的问题。

整个物流配送网络包括配送节点的实体网络和客户网络。对于一个第三方物流企业而言，物流服务的质量与其构建的物流服务的网络是密不可分的。由于配送中心服务质量的信息会在客户网络之间进行传播，良好的服务口碑能够提高客户对企业提供的物流配送服务的认同度，从而吸引更多客户选择该企业。但是当整个网络中的客户达到一定规模时，物流企业需要扩大自己的物流实体网络，即需要新建配送中心以满足客户要求。

在病毒传播模型中，一般用节点表示疾病传染或感染的个体，如果两个个体之间可以通过某种方式直接发生传染与被传染关系，就认为这两个个体之间存在连接，这样就得到了病毒传播网络的拓扑结构，进而可以建立相关模型来研究这种传播行为。将这种研究疾病传播的方法借鉴到对配送服务信息的传播网络研究中，将客户网络的增长过程看成是服务信息在客户之间的传播，用节点表示已接受该配送中心服务的客户，如果两个节点之间具有通过某种方式完成的传播关系，则可以认为两者之间存在连接，进而得到物流服务信息传播网络的拓扑结构与病毒传播网络拓扑结构具有同样特性的结论。

因此，本文以经典的SIR模型为基础，通过建立物流配送网络节点的饱和度模型，确定物流配送网络中节点的分支条件，并确定物流配送网络节点饱和度的影响因素。

二、国内外文献综述

经典的SIR模型最早是由康帕斯和麦肯德里克（Kermark&Mckendrick，1927）建立的，用来描述黑死病在伦敦的传播规律，对于得病治愈后获得免疫力而不能再次被传染的传染病类型，用SIR模型表示。国内外的学者对SIR模型的相关临界值进行了研究，并将其应用在不同领域，这在一定程度上对SIR模型的理论进行了深化，并取得了许多显著成果。王文迪（Wang Wend）[1]给出了平衡点的稳定性，研究了疾病持续的问题；1979年库克（Cooke）[2]得到了带有感染力的SIR模型；伯莱塔和匡（Beretta&Kuang）[3]发展了高次超越多项式稳定性方法；查淑玲[4]提出当健康者的比例大于有效传播效率时，提高卫生水平和传染病的治愈率可以控制疾病的蔓延。此后，夏立标[5]考虑了一类短暂免疫疾病的特点，通过建立具有时滞的SIR模型来研究无病平衡点；王建军、张晋珠、靳祯[6]建立了一类具有饱和发生率的传播模型，对确定疾病是否流行的阈值进行了研究；在此基础上，夏承遗、马军海、陈增强[7]建立了有传染媒介因素的SIR模型；续婷、朱烽[8]对有效传播效率的临界值进行了研究。

现阶段，学者们将SIR模型很好地应用在了医学、舆论传播、计算机病毒传播和经济等方面，解决了相应领域的许多问题。其中，在医学领域，李、胡、王（Li X、Hu Z、Wang W）等人[9]、[10]、[11]、[12]介绍了一种以治疗资源有限为前提的SIR模型；在预防和控制传染疾病的模型研究中，卢、池（Lu Z、Chi X）等人[13]建立了以人口数量恒定为前提的SIR模型；朱玑、李维德、朱凌峰[14]研究了疾病灭绝的阈值条件。为了使模型能够更好地在现实的疾病控制中应用，一些学者在研究过程中引入了真实数据，使SIR模型更加具有实际意义。霍阔、李世霖[15]采用墨西哥真实病例数据；陈端兵等人[16]引入已有的H1N1流感病毒数据。为研究疾病传播的阈值，运用 SIR 模型的分支过程理论[17]、[18]、[19]和SIS模型的平均场理论[20]、[21]，分别得到了疾病的传播阈值；韩华、马爱娜、赵夏、黄樟灿[22]提出了一种具有远程感染机制的传染病模型SIRS，求解得出在均匀网络上的传播临界值和最终感染密度的精确值。在舆论传播方面，随着SIR模型在病毒传播方面的应用，人们发现在社会网络中，谣言的传播与病毒的传播具有相似的动力学特征，所以学者们将SIR模型应用于舆论传播，以找出控制这种舆论传播的途径。杨、吴、周（Yang H X、Wu Z X、Zhou CS）[23]提出如果个体间的观点相差太大，则两者之间的联系就可能减少的观点；在此基础上，郭强等人[24]发现了在无标度网络上的舆论传播行为更容易达到一致；曾祥平等[25]建立了一个基于元胞自动机的网络舆论激励模型。在计算机病毒传播方面，珂芬特（Kephart）等人[26]在1991年第一次用传染病学数学模型对计算机病毒的传播进行了初步分析；在此基础上，冯丽萍等[27]提出了一种改进的具有预先免疫措施的SIR计算机病毒传播模型。在经济方面，马芳等[28]重点考察购买行为在人际圈中的传染扩散，并建立了四类数理模型；秦效宏、罗丙能[29]将营销学原理和传播临界值理论相结合寻找扩散阈值减小的方法。

但是，SIR模型在经济领域的应用，相对于医学和舆论传播、计算机病毒传播这三方面的应用还不够成熟，而在物流领域尚无应用。通过研究发现物流网络属于复杂网络，因此，将SIR模型应用在物流领域将具有很大的发展空间。因此，利用SIR模型与方法定量研究物流网络节点形成机理及规律，并以此来指导物流企业规模扩张和物流行业发展成为目前急需解决的重要课题。而配送网络节点服务质量传播过程与病毒传播特性相似，符合病毒传播机理与规律。利用SIR模型对配送网络节点形成机理和规律进行量化研究，成为研究配送网络节点形成机理和规律的重要方法。

三、物流配送网络节点服务客户饱和度建模假设

在以前的研究中我们了解到，一个包含物流实体网络和客户网络的物流配送网络符合无标度网络的演化特性，[30]同时物流服务信息传播网络的拓扑结构与流言传播、病毒传播网络拓扑结构具有同样的特性。随着配送实体网络服务质量的提高，良好的服务质量口碑会在客户之间进行传播，经过一段时间后，得到客户对企业提供的物流配送服务的认同，从而吸引更多客户选择该企业为其服务。随着时间的推移，配送实体网络服务的客户会越来越多，当客户增加到一定程度后，配送实体网络的服务水平和服务效率会无法满足客户的要求，客户就会选择其他的企业开展物流服务，因此在这个网络中客户网络呈现动态变化的特性。在物流企业的实际运作过程中，为了能够留住这些客户，物流企业往往会选择建立另一个配送节点来分担部分原有节点的业务，即通过扩大网络来增加物流配送实体网络的服务能力。在某个局域的配送网络中，配送节点服务的信息不断在客户之间传播，由于传播过程与流言传播、病毒传播的过程相似，因此，可以通过建立SIR模型的方法来找出局域配送实体网络配送节点所服务客户的饱和值。

根据前面的论述，在建立配送节点服务客户饱和度模型时需要符合以下假设：

假设1：物流配送网络符合无标度网络的演化特性；

假设2：在一个局域的网络中物流服务质量信息不断在客户之间进行传播；

假设3：物流配送网络不断扩展；

假设4：遗失的客户经过一段时间后，还有可能成为该区域的服务客户。

四、物流配送网络节点服务客户饱和度模型构建

经过前面的论证得知，物流服务信息的传播特性与疾病传播特性有相似的原理和结构，因此借鉴疾病传播模型来构建物流配送网络服务客户饱和度模型。物流配送网络中物流服务信息的传播过程遵循的是易染（S）→感染（I）→免疫（R）的SIR模型。将物流配送网络的SIR分别定义为：S（客户网络中的潜在客户，简称潜在客户）、I（客户网络中已经接受配送网络服务的客户，简称服务客户）、R（对目前配送网络的服务不满意，成为这个配送网络的遗失客户，简称遗失客户）。本文应用SIR模型从客户服务质量传播的角度对配送网络服务客户的饱和度进行建模，得出在物流服务信息传播过程中，何时该配送网络所服务的客户达到饱和，从而需要新建配送节点以满足客户的需求。

将无标度网络病毒的传播机理和配送网络的特性综合考虑，由于客户的生成过程符合无标度网络的生成规律，即物流服务质量的信息在无标度网络中进行传播。利用无标度网络病毒传播机理中的传播动力学来研究一个配送中心所服务客户的饱和值。

由于一个随机选取的配送节点倾向于连接关键点或连接度大的配送中心，因此节点度大的配送中心更容易开拓新的客户，从而导致比均匀网络上更快的网络拓展速度。由于配送网络不是简单、均匀的网络，考虑非均匀网络和配送网络的传播特性，建立如下模型。[31]、[32]、[33]

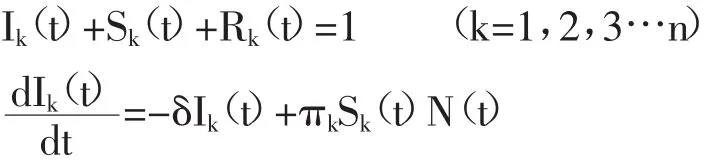
n为网络中节点的最高度值，π为配送中心的服务信息在客户间的有效传播速率，γ为潜在客户转向服务客户的概率，δ为服务客户转向遗失客户的概率，k为节点的度。

随着时间的推移，配送实体网络服务的客户会越来越多，当客户增加到一定规模后，配送实体网络的服务水平和服务效率会无法满足客户的要求，会不断有顾客流失。在这个时候已经接受配送中心服务的客户密度最终会达到最大，这时意味着配送中心对服务客户的服务能力达到了饱和状态，此时根据以上叙述，可以得出已经接受配送中心服务的客户密度在一定时刻会达到饱和，即存在一个最大的Imax，而此时则令：

令已经接受某配送中心节点服务的度值为k的客户的密度为ρk。由实际情况可知，ρk≥0，则可取其中进一步推导出

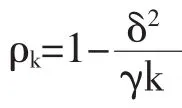
式中，ρk表示接受某配送中心服务的度为k的客户的饱和值。

将配送中心服务的所有客户节点加和，就得到了配送中心服务不同节点度的客户的饱和值。

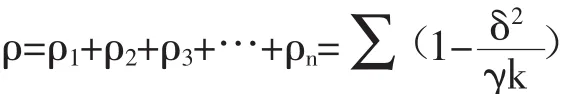
五、结 论

本文通过对无标度网络中病毒的传播机理和物流配送网络中服务质量信息在客户之间传播机理相似性的论证，将病毒传播模型应用到物流配送网络中服务质量的传播之中，试图解决配送节点服务客户的饱和度问题。文中以无标度网络的SIR模型为基础，改变了经过一段时间后原有模型中病毒移除率为100%的假设，重新定义了在服务质量信息传播中的相关变量，在包含所有不同节点度的客户情况下，构建配送节点服务客户饱和度的理论模型。

研究发现，以物流服务质量信息传播为视角，物流配送网络配送节点服务客户的饱和度受到服务质量传播率、网络规模及网络类型的影响，随着传播率的加大，配送节点服务客户的饱和度会增加，随着网络节点平均度数的增加，配送节点服务客户的饱和度也会增加。

[1]Wang Wend，Mulone G．Threshold of Disease Transmission in a Patch Environment[J]．Journal of Mathematical Analysis and Applications，2003，285（1）：321-335．

[2]K．Cooke．Stability Analysis for a Vector Disease Model．Rocky Mount.J.Math，1979（7）：253-263．

[3]E．Beretta，Y．Kuang．Geometric Stability Switch Criteria in Delay Differential Systems with Delay Dependent Parameters[J]．SIAM J.Math.Anal，2002，33：1144-1165．

[4]查淑玲．传染病的SIR模型[J]．山西中医学院学报，2003，2（4）：2-3．

[5]夏立标．带时滞的传染病动力学模型的平凡解分析[J]．大庆师范学院学报，2008，5（28）：68-70．

[6]王建军，张晋珠，靳祯．具有饱和发生率的SIR模型的持久性和稳定性[J]．中北大学学报，2008，6（29）：480-485．

[7]夏承遗，马军海，陈增强．复杂网络上考虑感染媒介的 SIR 传播模型研究[J]．系统工程学报，2010，6（25）：818-823．

[8]续婷，朱烽．BA无标度网络中的SIR模型[J]．数学的实践与认识，2011，11（41）：254-256．

[9]Li X，Li W，Ghosh M．Stability and Bifurcation of an SIR Epidemic Model with Nonlinear Incidence and Treatment[J]．AppliedMathematical and Computation，2009，2（10）：141-150．

[10]Hu Z，Liu S，Wang H．Backward Bifurcation of an Epidemic Model with Standard Incidence Rate and Treatment Rate[J]．Nonlinear Analysis：Real World Applications，2008，9：2302-2312．

[11]Wang W．Backward Bifurcation of an Epidemic Model with Treatmen[J]．Mathematical Biosciences，2006，201：58-71．

[12]Zhang X，Liu X．Backward Bifurcation of an Epidemic Model with Saturated Treatment Function[J]．J Math Appl，2008，348：433-443．

[13]Lu Z，Chi X，Chen L．The Effect of Constant and Pulse Vaccination on SIR Epidemic Modelwith Horizontal and VerticalTransmission[J]．Mathematical and Computer Modeling，2002，36：1039-1057．

[14]朱玑，李维德，朱凌峰.基于SIR传染病模型的不同控制策略比较 [J]．北华大学学报（自然科学版），2011（6）：265-269．

[15]霍阔，李世霖．甲型H1N1流感传播的SIR模型研究[J]．湖南工业大学学报，2010（7）：40-42．

[16]陈端兵，黄晟，尚明生．复杂网络模型及其在疫情传播和控制中的应用研究[J]．计算机科学，2011（6）：118-121．

[17]BarthelemyM，BarratA，Pastor-Satorras R，et al．Velocity and hierarchical spread of epidemic outbreaks in scale-free networks[J]．Physical Review Letters，2004，92：178-701．

[18]Manojit Roy，Rober D Holt．Effects of Predation on Host-pathogen Dynamics in SIR Models[J]．Theoretical Population Biolo-gy，2008（73）：319-331．

[19]Li Xuezhi，Li WenSheng，Mini Ghosh．Stability and Bifurcation of an SIR Epidemic Model with Nonlinear Incidence and Treatment [J]．Applied Mathematics and Computation，2009，210：141-150．

[20]Su Rui，He Daihai．Using Content 1．5 to Analyze an SIR Model for Childhood Infectious Diseases [J]．Communications in Nonlinear Science and Numerical Simulation，2008（13）：1743-1747．

[21]Zhang Xun，Liu Xianning．Backward Bifurcation and Global Dynamics of an SIS Epidemic Model with General Incidence Rat and Treatment[J]．Nonlinear Analysis，2009（10）：565-575．

[22]韩华，马爱娜，赵夏，黄樟灿．具有远程感染机制的SIRS 传播模型及仿真[J]．武汉理工大学学报，2010（2）：141-145．

[23]Yang H X，Wu Z X，Zhou C S，et al．Effects of Social Diversity on the Emergence of Global Consensus in Opinion Dyna-mics[J]．Phys Rev E，2009，80：46-108．

[24]Guo Q，Liu J G，Wang B H，et al．Opinion Spreading with Mobility on Scale-free Networks[J]．Chin Phys Lett，2008，25（2）：377．

[25]曾祥平，方勇，袁媛，杨玲，肖志宇．基于元胞自动机的网络舆论激励模型[J]．计算机应用，2007，11：2686-2688．

[26]Kephart JO，White SR．Directed Graph Epidemiological Modelof Computer Viruses[M]//Proceedings of the 1991 IEEE Symposium on Security and Privacy．Washington DC：IEEE Computer Society，1991：343-359．

[27]冯丽萍，王鸿斌，冯素琴．改进的SIR计算机病毒传播模型[J]．计算机应用，2011（7）：1891-1893．

[28]马芳，晁钢令．基于SIR模型的消费者购买行为人际扩散研究[J]．现代管理学，2011（6）：92-112．

[29]秦效宏，罗丙能．复杂网络理论在企业品牌营销中的应用研究[J]．中国市场，2010（18）：49-50．

[30]张旭凤，张永安．物流配送网络的无标度网络特征研究[J]．物流技术，2011，30（7）：97-100．

[31]Diekmann O，Heesterbeek J A P．Mathermatical Epidemiology of Infectious Diseases：Model Building Analysis and Interpretation[M]．New York：John Wiley and Sons，2000：79．

[32]Anderson R M，May R M．Infectious Diseases in Humans[M]．Oxford：Oxford University Press，1992：57．

[33]Moreno Y，Pastor Statorras R，et al．Epidemic Outbreak in Complex Heterogeneous Networks[C]．Eur：Phys．J．B，2002，26：521-529．