改进BISQ模型的双相介质地震波场数值模拟及频散校正

周竹生，唐磊

(中南大学 地球科学与信息物理学院，湖南 长沙，410083)

相对单相介质而言，双相介质能够更好地描述实际地层结构和性质，因此，双相介质的数值模拟更有利于实际介质中地震波传播规律的认识和研究。在双相介质的早期研究工作中，Biot假设孔隙介质理论中的固体与流体的相对运动属于Poiseuille型流动[1-2]，然而，随着双相介质研究的不断深入，研究发现孔隙介质中的流体还存在一种对地震波衰减和频散起关键作用的流动方式即喷射流动。其中，Biot流动力学机制描述的是宏观现象，而喷射流动机制描述的是局部特征。Dvorkin等[3]将这 2种机制结合起来，提出了BISQ模型，使得模型结构更贴近实际。Mamadou[4]提出改进BISQ模型，其优势在于在描述流体压力的表达式中不再含有不便于实际描述的微观参量(如特征喷射流动长度)，更加方便于地震波波场模拟的实现。本研究采用交错网格有限差分法对改进BISQ模型的双相介质地震波场进行数值模拟。数值模拟方法的共性是需要在时空域进行网格离散，以差分代替微分，由此所得到的地震波场必然存在数值频散现象。为了压制数值频散，本研究利用通量校正传输(FCT)技术修正了交错网格有限差分算法，确保在满足一定计算精度的前提下，可以采用较低的差分阶数，以提高计算效率。

1 基本方程

1.1 改进BISQ模型的双相介质弹性波动方程

在时空域内，基于改进BISQ模型的二维各向同性双相介质弹性波动方程可以表示为[4]:

1.2 一阶速度-应力方程

在二维情况下，基于改进BISQ模型的双相介质运动平衡方程为：

进一步推导，将位移分量对时间的一阶导数换成质点振动速度分量，得到一阶速度-应力方程为：

2 一阶弹性波方程高阶差分近似

2.1 时间域的2M阶差分近似

在使用交错网格法求解一阶速度-应力方程时，速度和应力分别是在t+Δt/2和t时刻进行计算的，对于速度与应力分量Vi和σij，利用Taylor公式得到2M阶精度的时间差分近似格式：

式中：Δt为时间步长；O(Δt2m)为高阶无穷小量，当M=1时，上式即为传统的二阶差分精度近似。

2.2 空间域的2N阶差分近似

在计算空间导数时采用下式所示的 2N阶差分近似表达式：

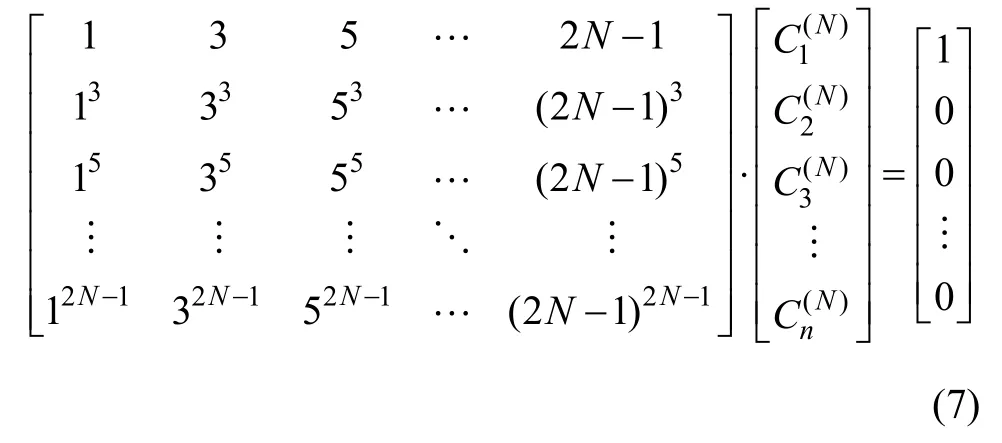
2.3 交错网格高阶有限差分格式的构建

对一阶速度-应力方程进行高阶差分近似，构建了空间2N阶和时间2阶精度的有限差分格式，其中：i，j和k分别表示x，z和t的离散序号；U，W，P，Q 和 S 分别表示固相 vx，vz，σxx，σzz和 σxz；u，w，F和R分别表示流相的Vx，Vz，S和P。

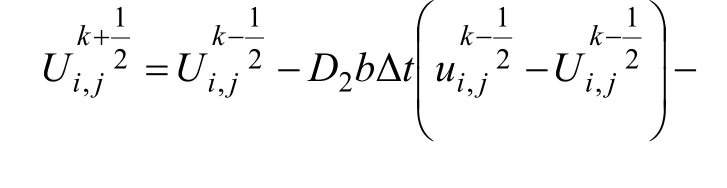
3 一阶方程FCT有限差分算法

Boris和 Book发展的通量校正传输方法(FCT)成功应用于声波方程[15]，FCT的基本思路是将修正的漫射应用于频散传输格式。在进行校正过程中分为漫射和反漫射2个阶段，计算的波场被改变以压制数值频散引起的伪波动。对于一阶速度-应力波动方程(8)，通过交错网格差分计算得到 k+1时刻的速度和应力值，为了提高计算效率，只需对差分计算得到的速度分量，，和的值进行校正。

(1) 计算k-1时刻的弥散通量：

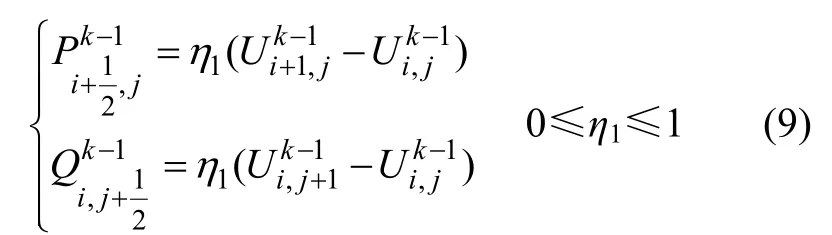
式中：η1为漫射参数，它是常量或一个线性函数，其取值取决于有限差分阶段频散误差。

(2) 计算k+1时刻的弥散通量：

式中，η2的取值与η1不同。这是因为振幅和分辨率的损失主要有2方面的原因：一是传统有限差分运算引起的频散，二是人为加入的漫射。反漫射运算不仅要补偿人为加入漫射引起的损失，而且要补偿传统有限差分运算带来的振幅损失。

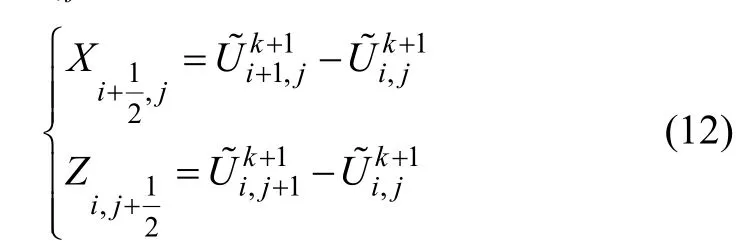
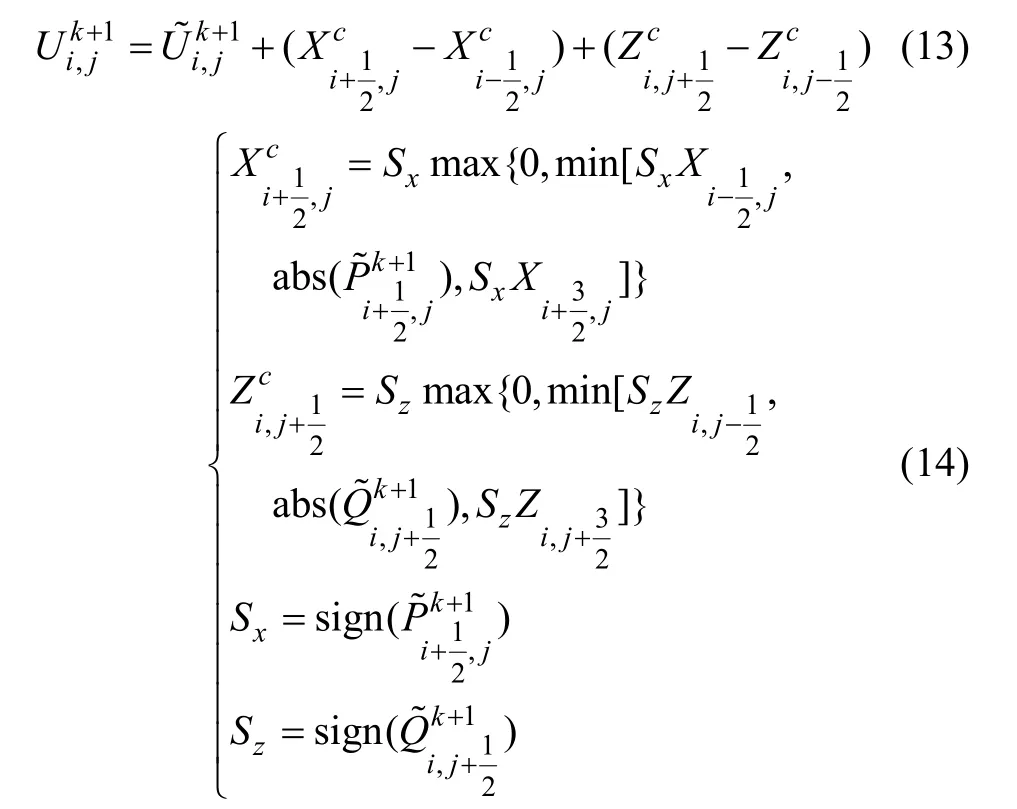
4 波场数值模拟及频散校正

4.1 波场模拟

为检验模拟算法的正确性，建立一个各向同性双相介质均匀半空间模型，模型网格点数为200×200，模拟过程中为消除人工边界的影响。采用Cerjan等[8]提出的吸收边界条件，为保证计算过程中的稳定性，选取空间网格间距为5 m，时间间隔为5 ms，震源位于模型中心，采用主频为30 Hz的雷克子波，模型的固体参数为：拉梅系数 12.6 GPa，剪切模量为6.72 GPa，固体体积模量为56.7 GPa，密度为2 822 kg/m3，耦合附加密度为85 kg/m3，纵波速度为3 km/s，横波速度2 000 m/s；流体参数：体积模量为1.51 GPa，密度为 554 kg/m3，孔隙率为 0.248 8，黏滞系数为1×10-6Pa·s，渗透率为 15 md。

采用精度为 O(Δt2+Δx4)和 O(Δt2+Δx16)的交错网格有限差分法，对固体和流体的水平分量和垂直分量分别进行计算，结果分别如图1和图2所示。

从图1和图2可以看出：在双相介质中存在第二类纵波，从内到外依次为慢纵波(p)，横波(S)和快纵波(P)，其衰减规律明显不同于第一类纵波，第一类纵波在固相和流相都引起较强的振动，第二类纵波引起较弱的固相振动，较强的流相振动，这种关系取决于双相介质的性质。其中第一类纵波的相位在固相和流相部分是相同的，第二类纵波的相位在固相和流相部分则相反。通过图1与图2对比可以发现：在时间差分精度一定时，空间差分精度阶数较低时，频散严重，随着阶数的增加，频散降低，波场模拟的精度逐渐提高。说明采用交错网格高阶差分能够对数值频散起到一定的压制。

4.2 加FCT修正的交错网格差分法进行波场模拟及频散校正

图3和图4所示分别为利用加FCT修正的不同精度的交错网格差分法进行波场模拟得到的波场快照图。与未进行FCT修正的图1和图2对比，可以看到频散现象得到明显地压制，说明FCT方法能够有效压制在计算过程中产生的数值频散，采用低阶精度的差分方程加FCT法修正后也可以得到较高阶精度的正演模拟结果。交错网格高阶差分与FCT方法相结合，在保持波场特征情况下能有效提高波场模拟的精度和计算效率。

图1 100 ms时波场快照(时间2阶，空间4阶)Fig.1 Snapshot of 100 ms (two-order time and four-order space)

图2 100 ms时波场快照(时间2阶，空间16阶)Fig.2 Snapshot of 100 ms (two-order time and sixteen-order space)

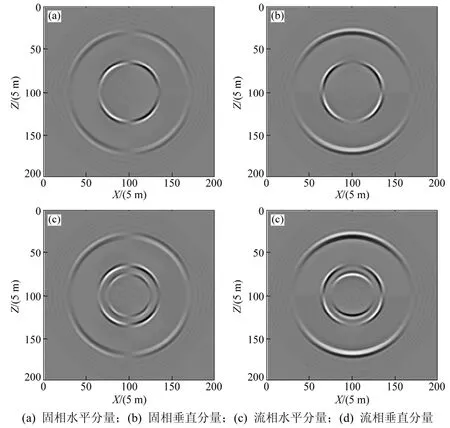
图3 FCT修正后的100 ms波场快照(时间2阶，空间4阶)Fig.3 Snapshot of 100 ms (two-order time and four-order space) by using FCT

图4 FCT修正后的100 ms波场快照(时间2阶，空间16阶)Fig.4 Snapshot of 100 ms (two-order time and sixteen-order space) by using FCT

5 结论

(1) 将交错网格差分法运用到各向同性双相介质中，给出不同时间和空间精度的一阶速度-应力波动方程交错网格差分算法格式，并提出带FCT修正的交错网格差分算法，运用交错网格差分算法实现各向同性双相介质地震波场正演数值计算。

(2) 双相各向同性介质中存在快纵波、慢纵波和横波，得到3种波在不同相介质中表现的波场特征。

(3) 对比不同差分精度计算得到的波场快照图，当时间差分精度固定时，空间差分精度随着阶数的增加，频散降低，差分精度的提高对频散起到压制作用。

(4) FCT方法能有效压制在计算过程中产生的数值频散，用低阶精度的差分方程也可以得到高阶精度的正演模拟效果，并且计算效率也得到了很大提高。

[1] Biot M A. Theory of propagation of elastic waves in a fluid-saturate porous solid, low-frequency range[J]. J Acoust Soc Amer, 1956, 28: 168-178.

[2] Biot M A. Theory of propagation of elastic waves in a fluid-saturate porous solid, higher-frequency range[J]. J Acoust Soc Amer, 1956, 28: 179-191.

[3] Dvorkin J, Nur A. Dynamic poroelasticity: A unified model with the squirt and the Boit mechanisms[J]. Geophysics, 1993, 58(4):524.

[4] Mamadou S. Acoustic wave propagation in saturated porous media: Reformulation of the Biot/Squirt flow theory[J]. Journal of Applied Geophysics, 2000, 44(4): 313-325.

[5] 孟庆生, 何樵登, 朱建伟, 等. 基于 BISQ模型双相各向同性介质中地震波场数值模拟[J]. 吉林大学学报: 地球科学版,2003, 33(2): 217-196.MENG Qing-sheng, HE Qiao-deng, ZHU Jian-wei, et al.Seismic modeling in isotropic porous media based on BISQ model[J]. Journal of Jilin University: Earth Science Edition,2003, 33(2): 217-196.

[6] 刘洋, 李承楚, 牟永光. 任意偶数阶精度有限差分法数值模拟[J]. 石油地球物理勘探, 1998, 33(1): 275-284.LIU Yang, LI Cheng-chu, MOU Yong-guang. Finite-difference numerical modeling of any even-order accuracy[J]. OGP, 1998,33(1): 1-10.

[7] 董良国, 马在田, 曹景忠, 等. 一阶弹性波动方程交错网格高阶差分解法稳定性研究[J]. 地球物理学报, 2000, 43(6):853-861.DONG Liang-guo, MA Zai-tian, CAO Jing-zhong, et al. A study on stability of the staggered-grid high-order difference method of first-order elastic wave equation[J]. Chinese Journal of Geophysics, 2000, 43(6): 853-861.

[8] Cerjan C, Kosloff D, Kosloff R, et al. A nonreflecting boundary condition for discrete acoustic and elastic wave equation[J].Geohysics, 1985, 50(4): 705.

[9] 牟永光. 储层地球物理学[M]. 北京: 石油工业出版社, 1996 27-38.MOU Yong-guang. Reservoir geophysics[M]. Beijing: Oil Industry Press, 1996: 27-38.

[10] 杨宽德, 杨顶辉, 王书强. 基于Biot-Squirt方程的波场模拟[J].地球物理学报, 2002, 45(6): 853-861.YANG Kuan-de, YANG Ding-hui, WANG Shu-qiang. Wavefield simulation based on the Biot-Squirt equation[J]. Chinese Journal of Geophysics, 2002, 45(6): 853-861.

[11] 吴国忱, 王华忠. 波场模拟中的数值频散分析与校正策略[J].地球物理学进展, 2005, 20(1): 58-65.WU Guo-chen, WAN Hua-zhong. Analysis of numerical dispersion in wave-field simulation[J]. Progress in Geophysics,2005, 20(1): 58-65.

[12] Dablain M A. The application of high differencing to the scalar wave equation[J]. Geophysics, 1985, 51(1): 54-66.

[13] XIAO Shao-ping. An FE-FCT method with implicit functions for the study of shock wave propagation in solids[J]. Wave Motion,2004, 40: 263-276.

[14] TONG Fei. Finite-difference modeling and depth-migration via flux-corrected transport[J]. SEG Expanded Abstracts 1993, 12(5):1074-1077.

[15] Book D L, Boris J P, Hain K. Flux-corrected transport II:Generalization of the method[J]. J Comput Phys, 1975, 18:248-283.