基于奇异值求通解方法进行基因调控网络构建
2012-07-31沈威郑明刘桂霞邢翀吴佳楠周春光周柚
沈威 ,郑明,刘桂霞,邢翀,吴佳楠,周春光,周柚
(1. 吉林大学 计算机科学与技术学院,吉林 长春,130012;2. 北华大学 计算机科学技术学院,吉林 长春,132021)
随着互补基因技术(cDNA)和微阵列技术的进步,人们已经能够在整个基因组范围内进行基因调控网络的构建。这些通过实验获得的数据提供了在一些特定时间点各种不同的生化环境下基因表达的、很有价值的描述。并且这些数据让研究者能从基因的时序表达值下推断基因调控网络。尽管如此,需要的基因调控网络是存在于基因组中的成千上万的基因所构成的网络,极其复杂。所以,在系统生物学中一项极具挑战的工作就是从各种数据尤其是时序数据中推断出基因调控网络。在可观测系统和从算法中获得的网络之间是存在差异的,这种差异导致了算法精确度的差异,目前很难提供一个高度精确的算法来实现对任意实验数据的网络推断。尽管如此,研究更精确的网络推断模型仍然是生物信息学的研究热点。许多方法被提出并应用在基因调控网络推断上,这些方法包括布尔网络[1]、贝叶斯网络[2-3]和微分方程模型[4]等。布尔网络提供了一种网络结构关系的概念层方法,网络一般规模庞大,常常包含成百上千的基因,但是,网络中节点的状态只有开和关2种状态。贝叶斯网络是一种能够描述网络关系的概率模型,网络模型中每条边都存在1个概率,贝叶斯网络的图形构成的是1个有向无环图,节点一般包括几十个节点,规模适中。微分方程模型则是一种高度精确的网络构建模型,以变化率的形式表示出各个基因的影响关系,是一个动态方程组。 这种方式构成的网络往往只包含几个基因,一般在20个以内,所构成的网络在数学上最精确,即规模小而精。但是无论采用哪种方法,仍然存在精度不高的问题,因此,需要一个更好的方法来进一步改进微分方程模型。改进策略之一是改变方程的形式,如把方程中某个参数进行分解或改变,更可以把微分问题化为积分问题[5]等,但这种策略在本质上并没有改变精度。另一种改进策略是引入奇异值分解(SVD)[6]的方法。在运算过程中把方程组中表达数据所构成的矩阵或其转置矩阵进行分解,之后进行矩阵运算并得到符合奇异值分解规则的解即权值矩阵作为最终网络结果。在多个基因的实验数据条件下,方程组的解往往并不唯一,而奇异值分解求出的是惟一解,这个解可能在无数解集中并不是最优解。针对这个问题,本文作者在通过奇异值分解求得的特解基础上求出符合奇异值分解规则的通解即解的集合,并把这个通解作为一个取值范围,结合改进形式的微分方程模型策略用优化算法求解和优化网络的权值矩阵并得出网络的最终结果。
1 算法的数学框架
用于推断网络的方法可以分为2步。首先,要使用奇异值分解方法来构建一个解的集合。这个集合是由符合方程组规律的解集所组成的,如果规模很大,一般提供通解。然后,在这个集合或标准下进行模型的优化,使用线性回归分析进行微分方程的求解,并最终得到所求网络。
为了简化,仅对稳态系统或者接近稳态的系统进行分析。构建网络的数学模型采用的是微分方程模型。这个模型可以简化为每个方程均为式(1)所示形式的方程所组成的方程组:

其中,xi(t)为基因i在时刻t的浓度;N为网络所包含基因的总数;wij为基因j对基因i进行影响的权值参数,这个值是正数时表示正调控,负数时表示负调控,0表示在一定阈值范围内可以视为不发生相互作用;bi表示在没有调控输入的情况下基因 i的变化,也包括了外界对基因i的刺激所产生的表达浓度的变化。
在实验中,可以提供一些恒定的外界刺激,即bi是恒定的。为了方便,更多的时候设定bi为0,即不施加任何外界刺激。然后,对N个基因在T个时间段进行测量,即得到所需数据,数据组织形式如下:

其中:x为基因表达浓度;下标表示基因标识,上标表示测试时间序列;共有N个基因、T个时间测试点。根据式(2),式(1)可以写成式(3)所示形式:

为了求出权值矩阵W,往往把方程组进行变形和改进,这可以在一定程度上提高精度,但要从根本上提高精度需要进行奇异值分解。可以将X矩阵进行奇异值分解:

其中:矩阵A是一个不必满足满秩条件的对角矩阵。为了计算方便,可以在计算过程中进行调整,使得矩阵A中对角线上的值是按照大小进行排序的。即非零值第1个值最大,其他值递减。后面的几个对角线上的值为0,非对角线上的值全为0。对角线上零值的个数可以为 0,即此矩阵可以为满秩矩阵。在式(4)中,奇异值分解得到的结果U与V都是正交矩阵,且都满足:
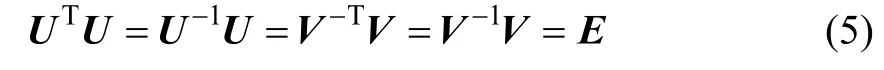
式中:E为单位矩阵。
对式(3)两边同时减BN×T,然后,方程两边同时右乘XN×T的逆矩阵,并把式(4)代入式(3),得到:

在式(6)中,并不是每个矩阵都存在逆矩阵,特别是矩阵 U,这里的逆矩阵指的就是广义逆矩阵[7]。在广义逆矩阵定义下,任意一个矩阵都存在其逆矩阵。但其广义逆矩阵往往不是方阵,更不是奇异阵。
由式(6)得到基因调控网络构建所需的权值矩阵W。研究者们一般就把此特解作为最终的网络结果,但该结果并不精确,因为符合式(6)条件的值很多,数量级很大,甚至无穷多解,即N>>T,这样所求的值其实并不一定是最优解。在计算过程中,最好能够尽可能多的得到解集或者取值范围,并使用优化算法进行计算。本文算法在特解的基础上,构造下式来求通解:

式中:C为任意常数。
构造了这个通解后,就可以得到所求解的取值范围,从而可以修改微分方程模型,并计算优化,在此范围内求得所求网络。
从式(1)出发对权值矩阵 W 进行变形。首先需要定义此算法的能量函数,即误差最小化函数。此误差为所求值和观测值之间的差:
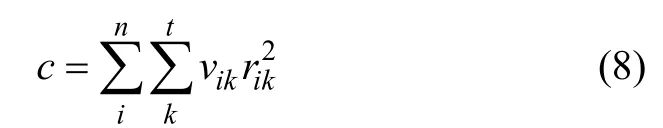
其中:rik为式(1)的残基;vik为rik的1个权值,则

从式(9)可以看出:rik符合残基概念。本文所要做的就是在式(7)所示的网络权值取值范围内使残基最小化。得到所要进行的目标之后,需要把方程进一步改进,以便提高效率,较少误差。在式(8)和(9)中,所需计算的只有wij,而网络中共有N个基因且权值矩阵W为一方阵,则所需计算的参数为N个。一旦基因数过于庞大,则所需计算的参数个数将随指数级增长,不适合求解,因此,需要把权值矩阵W进一步优化并分解,这样权值w将变为:

经过式(10)的转化之后,权值矩阵W中的值只与t和x这2个变量相关,从而使得计算非常简便。
优化算法方面,本文采用粒子群算法[8]和遗传算法[9]相结合的方式,通过最小化式(8),求得最小值,然后验证是否符合式(7)的方式,求得最终的网络。
2 算法的实现
本文算法的实现部分用Java语言编写,所用环境为MyEclipse 8.0版本。算法的流程步骤如下。
(1) 读取基因表达数据,其格式符合国际表达数据标准(MIAME[10])。
(2) 对已经读取的基因表达数据所构成的矩阵运用式(4)进行奇异值分解并得到式(4)中的U与V。
(3) 运用式(6)求得所需计算的权值矩阵W的特解W特,并根据式(7)求得W的通解W通。
(4) 随机生成大量权值构成粒子群算法和遗传算法的初始群体。并根据步骤(3)得到的取值范围淘汰不符合要求的随机权值。淘汰的权值重新生成,直到所有的随机权值符合W通的条件为止。
(5) 运用式(10)分解权值,将权值降维为只有2个变量的方程组。并运用遗传算法和粒子群算法(PSO)最小化式(8),得到最小值。
(6) 若步骤(5)计算得到的值符合 W通的条件则算法终止,否则进入步骤(5)。
算法流程图如图1所示。

图1 本文算法流程图Fig.1 Flow chart of proposed algorithm
3 实验结果与分析
3.1 测试方法
为了测试本文算法的效果,进行比较实验。比较对象为单纯使用式(1)的基本微分方程模型(方法 1)和代入式(10)的改进型微分方程模型(方法2)及本文模型(方法3)。这3种模型的比较实验将分为模拟数据实验和真实数据实验2部分。
采用 Bansal等[11]所提出来的正预测值(PPV)和敏感度(SE)评价算法优劣。
3.2 模拟数据实验
数据来源采用生成无标度网络[12]后微分方程逆向反推基因表达数据的方法进行计算获得。与随机生成的网络相比,无标度网络更符合基因调控网络的生物学现象。在生成的无标度网络中,每个节点的连接数都接近于幂率分布 p(k)~k。本文用增加重导向自增算法[13]进行构建。参数r设定为3,节点数N为20。根据这种算法和参数构建的网络如图2所示。在图2中,原点为节点0,逆时针依次为节点1,2,…,20。方块的为有向线段末端,指向被调控节点。网络生成以后,用式(1)来进行数据推断,所有的bi均设置为0。数据的时间点设定为 50。随机噪声参数设定为-0.5~0.5之间。
由图2所示的图模拟出基因表达数据后,经过运算得到结果如图3所示。在图3中,所表示的含义与图2的一样,不同的是圆圈代表的是自我调控关系。
为了避免结果巧合,运行程序100次,并把N的取值定为 20。计算后取平均值并评估算法的优劣。3种方法的比较结果如表1所示。
从表1可知:本文算法(即方法3)的正预测值和敏感度明显高于其他2种算法的结果,其运行时间也比其他2种方法的运行时间短。

图2 参数r=3,N=20的无标度网络图Fig.2 Scale-free network with parameter r=3, N=20

图3 根据图2所生成的数据所计算的基因调控网络图Fig.3 Gene regulatory network calculated with proposed algorithm from data simulated by Fig. 2

表1 3种算法模拟数据效果比较Table 1 Compared results of three kinds of algorithm in simulation data
方法2比方法1在运行时间上更有优势的原因在于方法2把方法1中的N2个参数化简为只有2个参数,使得运算时间大大缩短。本文方法为方法2提供了一个很好的候选解的集合,减少了方法2寻优的空间和运行时间,但是,由于奇异值分解运算本身消耗了一定的时间,因此,与方法2的运行时间相比,本文方法的运行效率略有提高。
3.3 真实数据实验
真实数据的计算采用的是 GEO[14]基因表达数据库上下载的基因表达数据,这里采用的是经典的酵母基因表达数据,即采用GDS38数据的子集,其表达的结果图可以从日本KEGG[15]数据库中的pathway里得到。这个数据包括3个子集,这3个子集包括3种实验条件:Alpha,elu和cdc15,它们分别包括18,14和24个时间点。抽取出来的1个网络子集如图4所示。经过本文算法计算,对应图4所生成的基因调控网络如图5所示。在图5中,所有的含义与图2中的一样,原点作为第1个初始点,圆圈表示自调控,方块表示被调控段。

图4 KEGG数据库的pathway中酵母基因调控网络的1个子集图Fig.4 A part of yeast cell cycle pathway available from KEGG

图5 用本文算法算得的基因调控网络图(对应图4)Fig.5 Gene regulated network calculated by proposed algorithm (according to Fig. 4)
根据式(1)和(10)的微分方程模型,运行100次后取平均值,最终结果如表2所示。
从表 2可以看出:本文算法(即方法 3)比其他 2种算法更优越。从运行时间上来看,本文算法比其他2种算法相比更小。与模拟实验结果相比,优势不是很明显。
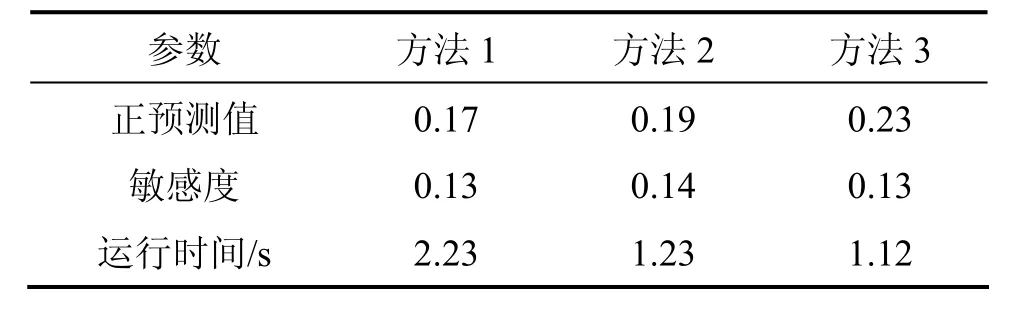
表2 3种算法运算真实数据结果比较Table 2 Compared results of three kinds of algorithm in real data
4 结论
(1) 提出了一种具有通解的构建基因调控网络算法。这种新的融合算法不仅在运算过程中提供了一个候选解的集合,使得运算过程中免去了非解的不必要计算,缩短了运算时间,同时,使得运算结果更精确。通过与其他2种传统微分方程模型算法的对比实验,证实了本文算法的效率较高,符合预期结果。
(2) 本文算法的目标是从有限的数据中得到最接近于真实的基因调控网络的结果,提高实验水平。但是,本文的基因调控网络算法整体的精度,还需进一步提高,这有待进一步研究。
[1] D’haeseleer P, Liang S, Somogyi R. Genetic network inference:from co-expression clustering to reverse engineering[J].Bioinformatics 2000, 16: 707-726.
[2] Dojer N, Gambin A, Mizera A, et al. Applying dynamic Bayesian networks to perturbed gene expression data[J]. BMC Bioinformatics, 2006, 7: 249.
[3] Beal M J, Falciani F, Ghahramani Z, et al. A Bayesian approach to reconstructing genetic regulatory networks with hidden factors[J]. Bioinformatics, 2005, 21: 349-356.
[4] Bansal M, Gatta G D, di Bernardo D. Inference of gene regulatory networks and compound mode of action from time course gene expression profiles[J]. Bioinformatics, 2006, 22:815-822.
[5] Eugene N, Emmanuel B. Regulatory network reconstruction using an integral additive model with flexible kernel functions[J].BMC Systems Biology, 2008, 2: 8.
[6] Nelson P A, Kahana Y. Spherical harmonics, singular-value decomposition and the head-related transfer function[J]. Journal of Sound and Vibration, 2001, 239(4): 607-638.
[7] Liang M L, Dai L F. The left and right inverse eigenvalue problems of generalized reflexive and anti-reflexive matrices[J].Journal of Computational and Applied Mathematics, 2010, 234:743-749.
[8] Brits R, Engelbrecht A P, van den Bergh F. Locating multiple optima using particle swarm optimization[J]. Appl Math Comput,2007, 189(2): 1859-1883.
[9] Chen D Y, Chuang T R, Tsai S C. Jgap: A java-based graph algorithms platform[J]. Software Pract Exper, 2001, 31(7):615-635.
[10] Tim F R, Philippe R S, Paul T S, et al. A simple spreadsheet-based, MIAME-supportive format for microarray data: MAGE-TAB[J]. BMC Bioinformatics, 2006, 7: 489.
[11] Bansal M, Belcastro V, Ambesi-Impiombato A, et al. How to infer gene networks from expression profiles[J]. Mol Sys Biol,2007, 3: 78.
[12] Barabási A L, Albert R. Emergence of scaling in random networks[J]. Science, 1999, 286: 509-512.
[13] Silva A C, da Silva J K L, Mendes J F F. Scale-free network with Boolean dynamics as a function of connectivity[J]. Phys Rev E,2004, 70(6): 66140-66147.
[14] Wilhite S E, Barrett T. Strategies to explore functional genomics data sets in IVCBI’s GEO database[J]. Methods Mol Biol, 2012,802: 41-53.
[15] KEGG Cell cycle-yeast-Saccharomyces cerevisiae[EB/OL].[2010-04-13].http://www.genome.jp/kegg/pathway/sce/sce0411 1.html.
