组合板剪切 粘结机理及承载能力试验
2012-07-30史晓宇陈世鸣裘子豪
史晓宇,陈世鸣,裘子豪
(同济大学 土木工程学院,上海200092)
压型钢板-混凝土组合板由带压痕、齿槽的压型钢板上浇混凝土构成.组合板常见的破坏方式是钢板与混凝土板交界面处的纵向剪切-粘结破坏.端部锚固明显改善了组合板的纵向剪切-粘结承载特性.
本文通过试验,研究了极限状态下部分剪切 粘结作用,揭示了组合板剪切-粘结破坏机理,给出了考虑端部锚固影响的承载能力简化计算的建议.
1 当前通用的设计方法
现行组合板纵向抗剪承载能力的设计主要有m-k法和部分连接法(τu,表示剪跨内的纵向剪应力)(图1)[1-2],如欧洲规范(EC 4),我国《钢-混凝土组合楼盖结构设计与施工规程》[3]和《高层民用建筑钢结构技术规程》[4]等.
m-k法中,组合板的纵向抗剪承载力采用纵向剪切 粘结破坏时支座截面的竖向力Vu,表示为
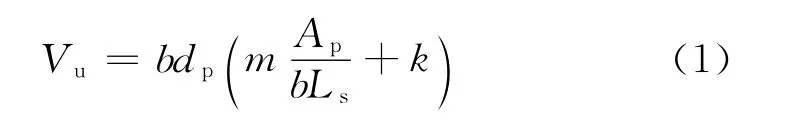
式中:b为板宽度,mm;dp为组合板的有效高度,mm,即截面受压区边缘到压型钢板形心的距离;Ap为压型钢板截面积,mm2;Ls为剪跨长度,mm;m和k是由试验确定的两个经验参数,N·mm-2.
部分连接法中,组合板纵向抗剪应力可通过与截面弯矩承载力对应的纵向剪切连接度来计算(图1):

式(2)及图1中:Nc为组合板受弯破坏时截面上混凝土的压力;Ncf为组合板呈塑性受弯破坏时混凝土的最大压力;η为Nc与Ncf的比值,表示组合板纵向抗剪连接程度;Lo为支座悬挑端长度;fcm为混凝土圆柱体抗压强度均值;fyp为钢板屈服强度;Mp,rm为完全共同作用时组合板的抗弯能力;M为试件纯弯段截面弯矩承载力;Mtest为试验测得的纯弯段抗弯能力;Vv为支座处竖向剪力.
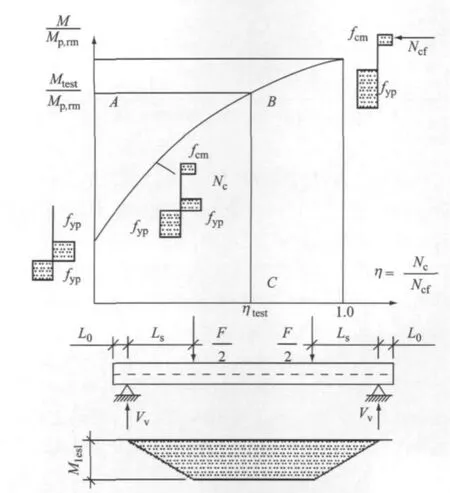
图1 部分连接方法Fig.1 Partial connection method
2 组合板弯曲试验
共进行了13块组合板的承载力试验,其中8块为无端部锚固的组合板,其余5块组合板均采用栓钉穿透钢板与支承钢梁焊接的端部锚固.试验采用华胤3WDECK压型钢板,厚度为0.9mm,实测屈服强度为315MPa.表1为构件编号和基本参数,试件见图2.
组合板混凝土强度等级为C25,剪力钉直径为19mm.组合板板宽920mm.钢梁支座采用HM300×200热轧H型钢,混凝土内放置φ5.5@200单层双向钢筋网,距混凝土板顶20mm.

表1 组合板试件分类及编号Tab.1 Groups and details of tested composite slabs

图2 组合板试件及截面构造(端部锚固试件)(单位:mm)Fig.2 Test specimens(with end anchorages)(unit:mm)
试验采用门式反力架,320kN液压千斤顶通过二级加载分配梁,对楼板作用两点集中线荷载(图2).
共采用10个位移计对组合板的挠度和端部滑移进行了实时记录,其中8个沿板跨方向布置以测量板的挠度;其余2个安装在端部,测量混凝土与钢板端部的相对滑移.沿板长,在混凝土板顶,混凝土内,压型钢板的上、下翼缘及斜腹板处均布置了应变片.混凝土板内应变通过在混凝土内预埋的钢筋和钢筋网上贴放应变片测得,在混凝土开裂前,钢筋应变代表此处混凝土的应变.端部锚固栓钉杆部两侧也贴有应变片.
对于无端部锚固的试件,荷载缓慢增加直至试件破坏;对于有端部锚固的试件,荷载先以每级2 kN逐渐增大,当荷载达到8kN左右,荷载缓慢增加直至试件破坏,试验数据进行连续自动采集.
3 试验结果及讨论
图3为试件的荷载—挠度曲线.试件1~8为无端部锚固的试件,9~13为端部栓钉锚固的试件.比较发现,端部锚固试件的承载和变形能力均有很大提高.

图3 试件荷载—跨中挠度曲线Fig.3 Load-deflection curves of specimens
图4 为典型试件的荷载—端部滑移曲线.端部滑移出现后,无端部锚固试件承载力迅速下降,端部锚固试件承载力仍有一定增加.试件两端部滑移出现时间及数值大小均不一致.
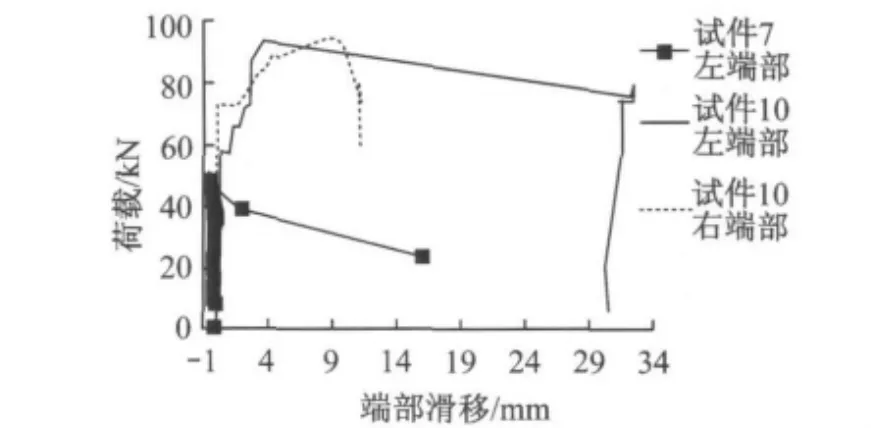
图4 典型试件荷载—端部滑移曲线Fig.4 Typical load-end slip curves of specimens
表2列出了各试件的极限荷载,根据EC 4对破坏类型进行了分类.表中Pu和Mu分别为极限状态下构件所受的荷载和跨中弯矩.各试件的极限弯矩均小于塑性抗弯强度设计值Mp,且都出现了混凝土与压型钢板的竖向分离和纵向滑移,即所有试件均发生纵向剪切-粘结破坏.

表2 试件破坏荷载及弯矩Tab.2 A summary of test results for load carrying capacities
试验发现:组合板纵向剪切粘结破坏分脆性和延性两种.脆性破坏时大部分裂缝宽度较大,大多分布在加载点附近区域.延性破坏的裂缝则主要分布在加载点附近和板中纯弯区域,裂缝发展更为充分细密.无端部锚固试件两种破坏模式均有发生,端部锚固试件则主要发生延性破坏.
组合板中混凝土受拉开裂后,该区域钢板与混凝土板交界面出现竖向分离和纵向滑移,导致组合板承载机理由完全粘结作用转变为部分粘结连接,钢板上翼缘及部分斜腹板区域由受拉变为受压.图5a显示了组合板较为典型的极限破坏状态:发生混凝土主裂缝,出现界面滑移和脱开,跨中及加载点附近下部钢板局部屈曲.图5b为端部锚固试件的端部栓钉底部钢板屈曲和撕裂剪切破坏.
组合板(试件5)钢板应力沿跨度的分布如图6和图7所示.界面滑移出现前,截面应变符合平截面假定,钢板与混凝土板共同承担外荷载,压型钢板全截面受拉;滑移出现后,该处钢板与混凝土板局部分离,混凝土与钢板不再完全共同作用,截面不再符合平截面假定,此时,钢板上翼缘相应部分受压,下翼缘及大部分斜腹板仍受拉;极限状态下,所有试件的钢板上翼缘及部分斜腹板局部受压屈曲,钢板下翼缘达到屈服强度.

图8为纵向剪切-粘结破坏前后组合板截面的应变和内力分布.图中,S为试件端部钢板与混凝土的相对滑移,界面的纵向剪力F可对截面混凝土受压区合力作用点取矩,由力平衡法来表示[5]:

式中:Ns为钢板的纵向拉力;P为竖向荷载;Mpr为压型钢板由于一部分截面受压而自身承受的弯矩,称为非组合弯矩;z为截面受拉合力与受压合力之间的距离,z表示截面上钢板受拉合力与混凝土受压合力之间的距离,其数值取决于截面的应力分布情况.混凝土开裂之前,截面应力分布服从平截面假定.随着荷载增加,混凝土受拉开裂导致钢板与混凝土交界面产生纵向滑移和竖向分离.

图8 组合板受力分析Fig.8 Load carrying state of a slab
因此,组合板截面受拉区合力与受压区合力的距离可由试验数据近似表示为

式(4)~(6)中:ycc为混凝土受压区高度;yss为钢板受拉区高度;hc为混凝土有效高度,取钢板上翼缘到板顶的距离;hs为压型钢板高度;h为组合板总高度;x1到x4为试验测得的截面不同高度处的钢板及混凝土板的应变.
非组合弯矩Mpr由图9的弯矩—曲率关系得到:


式(7)~(8)中:Es为钢板弹性模量;Is为钢板截面惯性矩;1/R为距支座x的板底曲率,根据几何相似关系求得;δx为测点的挠度.图9中,L为板跨度,θ和α为弯矩作用下相应截面的转角,P为集中力荷载,S1为相应测点处截面上钢板与混凝土的相对滑移.
试验中,沿板跨度方向设置了6个位移计、支座处设置了2个位移计以测量试件距支座x的挠度δx.测得的数据通过多项式拟合可得到试件的挠曲线.将测得的挠度及荷载值代入式 (7),(8)和(3),可得到组合板中对应测点试验中的纵向剪力.假设小区段内的纵向剪应力沿接触面均匀分布,得到:

式中,Nsi为组合板不同位置截面的纵向剪力;τi和Aconi分别为对应区段范围内的剪应力和接触面积.

图9 受弯组合板Fig.9 Slab under bending
图10 a为试件纵向剪力与支座竖向剪力的关系曲线.在竖向剪力达到最大值之前,纵向剪力与竖向剪力均近似呈线性关系.图10b为13个试件的纵向剪力与竖向剪力的比值和长细比Ls/dp(剪跨长度与板有效高度的比值)的关系,其线性回归近似式为

式中:VL为试件最大纵向剪力;Vu为半跨试件隔离体支座处竖向剪力,等于P/2(图8);n为一常数.

图10 试件纵向剪力与支座处竖向剪力关系Fig.10 Relationship between longitudinal shear force and vertical shear force at supports
4 考虑端部锚固纵向抗剪承载能力
4.1 试件纵向抗剪承载能力的评估(m-k法)
将式(10)代入式(1)可得纵向剪切 -粘结破坏时的纵向抗剪力为

令 m'=nm,k'=nk,式(11)可表示为

若剪跨内的纵向剪应力近似表示为τu=VL/bLs,式(12)又可表示为

根据纵向剪应力的概念,m'代表组合板交界面的机械咬合能力,k'代表摩擦能力.则式(13)表示了试件纵向剪应力的m-k关系.可推得最大纵向剪应力线性回归计算公式:无端部锚固试件:
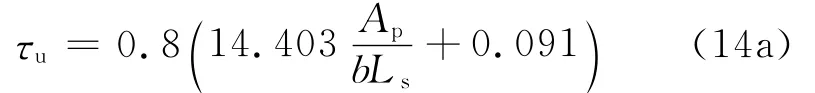
端部锚固试件:

4.2 试件纵向抗剪承载能力的评估(τu方法)
据部分连接法,组合板弯矩承载力表示为

式中:Ns为钢板的纵向拉力;Mpr为压型钢板承受的非组合弯矩.无端部锚固组合板的截面抗弯承载力M可按纵向抗剪连接程度η进行计算,对应不同的η,可计算得η-M/Mp曲线.
采用栓钉端部锚固,对纵向抗剪的贡献可取栓钉抗剪能力与端部钢板抗撕裂能力中的较小值[1].试验中组合板的端部剪切破坏为栓钉底部压型钢板的撕裂,其抵抗撕裂的能力Nr可以表示为

其中系数kφ由式(17)得到[1]:

式(16)~(17)中,dd0是栓钉根部环形焊缝的直径,可取栓钉杆直径的1.1倍;a为栓钉中心到钢板边缘的距离,不小于dd0的1.5倍;t是钢板的厚度;fy是钢板的屈服强度.
4.3 不同计算方法的比较及评估
根据试验和τu法可分别计算出极限纵向剪力Nc,并求得纵向剪应力τu,另外计算端部栓钉锚固对组合板纵向抗剪的贡献Nr(Nr代表了端部锚固影响导致的混凝土压力Nc的增大值),结果见表3.比较表明:与试验测值相比,无端部锚固试件,τu法计算的纵向抗剪能力偏于保守;而端部锚固的试件,τu法求得的试件10~12的Nr值有所高估.m-k法计算的τu回归公式与试验结果更为接近.

表3 不同计算方法求得的纵向抗剪能力比较Tab.3 Comparisons of longitudinal shear resistance obtained from various calculation methods
4.4 考虑端部锚固组合板弯矩承载力简化算法
为便于工程设计,据极限状态下组合板截面的应力分布,对式(15)进行修改,提出改进计算法.设任意抗剪连接程度η时,组合板截面弯矩承载力为

式中:η1和η2分别为钢板与混凝土相互作用以及钢板塑性弯矩的折减系数;fy为钢板屈服应力;As为压型钢板截面面积;Mpa为压型钢板的塑性抵抗弯矩.γap为钢板的部分作用系数,根据EC 4取1.1.
对于不同的压型钢板,可得到折减系数η1和η2,其数值与长细比Ls/dp以及端部锚固情况有关.本次试验采用的压型钢板折减系数η1和η2建议取值见表4.

表4 折减系数取值Tab.4 Recommended values for reduction factors
改进算法与试验的抗弯承载力比较结果见表5.另外,选择了几组其他研究者的试验结果进行了比较.结果表明,折减系数η1和η2的建议取值也可用于其他板型试件.对闭口型试件计算结果偏于保守.
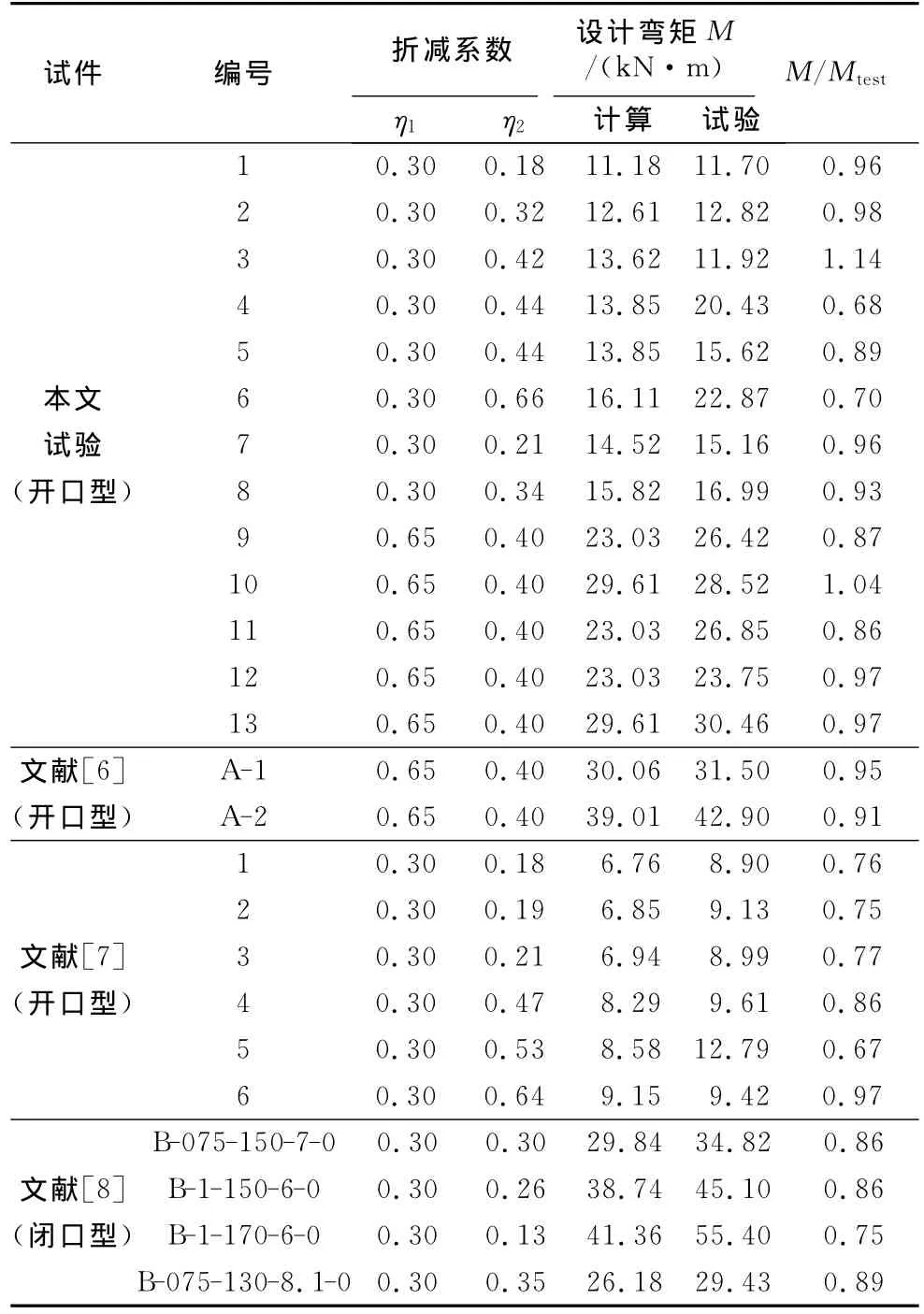
表5 改进方法和试验结果对比Tab.5 Comparisions between revised method and test results
5 结论
(1)组合板底部混凝土受拉开裂,导致压型钢板与混凝土界面剪应力增大,当剪应力超过纵向粘结力,界面出现局部纵向滑移和竖向分离,最终导致组合板的纵向剪切 -粘结破坏.
(2)组合板纵向抗剪主要由剪跨段提供,剪跨段越长,组合板的纵向抗剪能力发展得越充分.
(3)组合板的粘结破坏分为脆性和延性.无论脆性还是延性破坏,达到荷载峰值前,组合板纵向剪力与竖向荷载近似呈线性关系,其比值与试件长细比有关.
(4)提出了考虑端部锚固的组合板弯矩承载力的改进计算方法,计算结果与试验结果吻合较好.
(5)η1和η2建议取值可用于不同板型试件.闭口型试件计算结果偏于保守,需作进一步研究.
[1]EN1994-1-1 EC 4:design of composite steel and concrete structures,part 1.1:general rules and rules for buildings[S].Brussels:European Committee for Standardization.2004.
[2]ANSI/AASCE3——91 Standard for the structural design of composite slabs[S].New York:ASCE,1992.
[3]YB9238—92钢 混凝土组合楼盖结构设计与施工规程[S].北京:中国建筑工业出版社,1992.YB9238—92 Design and construction specification for steelconcrete composite floors[S].Beijing:China Architecture and Building Industry Press,1999.
[4]JGJ 99—98高层民用建筑钢结构技术规程[S].北京:中国建筑工业出版社,1999.JGJ 99—98 Technical specification for steel structure of tall building[S].Beijing:China Architecture and Building Industry Press,1999.
[5]Abdullah R,Easterling W S.New evaluation and modeling procedure for horizontal shear bond in composite slabs[J].Journal of Constructional Steel Research,2009,65(4):891.
[6]Chen S.Load carrying capacity of composite slabs with various end constraints[J].Journal of Constructional Steel Research,2003,59(3):385.
[7]Marimuthu V,Seetharaman S,Arul Jayachandran S,et al.Experimental studies on composite deck slabs to determine the shear-bond characteristic(m-k)values of the embossed profiled sheet[J].Journal of Constructional Steel Research,2007,63(6):791.
[8]杨文平,杨勇.闭口型压型钢板 混凝土组合板承载能力试验研究[J].建筑科学,2008,24(5):37.YANG Wenping,YANG Yong.Experimental study on bearing capacity of composite slabs with closed profiled steel sheeting[J].Building Science,2008,24(5):37.
