基于小生境的GEP新算法

莫海芳，李康顺，彭 川

（1.中南民族大学 计算与实验中心，湖北 武汉430074；2.华南农业大学 信息学院，广东 广州510642）

0 引 言

基因 表 达 式 编 程（gene expression programming，GEP）作为一种新的演化算法，在演化建模［1－3］，神经网络［4］和分类［5］等领域取得了很好的应用结果。但是，作为一种随机搜索算法，GEP也存在早熟和陷入局部最优的缺陷。很多学者对GEP进行了跟踪研究并提出不同的改进算法，其中避免算法过早收敛和提高算法收敛速度是改进的主要方向。

众所周知，群体多样性的过早缺失会导致算法早熟收敛。因此，能否保持合适的群体多样性水平，对算法的全局收敛性有直接的影响。文献［6］引入基因漂移和漂移抑制的概念，通过漂移抑制算子控制基因的过度漂移，同时保持种群的多样性。文献［7］提出基因空间均匀分布策略，提高初始种群的基因多样性，从而提高进化效率。文献［8］使用带权的函数符和终结符，以保证初始种群具有丰富的多样性，同时采用自适应的交叉和变异算子，维持进化过程中的种群多样性。但这种方法需要先验知识来设定染色体中各符号的概率。文献［9］采用变种群策略，在进化初期，采用较小规模的种群；进化过程中，引入新个体，增大种群规模，增加基因多样性。但是，增大种群规模也增加了GEP每代进化所耗费的时间。也有文献在GEP中用小生境技术保持群体的多样性［10－11］。

提出一种基于小生境的GEP新算法，该算法能够避免演化后期出现大量重复个体，使群体在整个演化过程都能保持个体的多样性。使得改进后的GEP新算法能有效的避免早熟收敛，提高算法的全局搜索效率。

1 基因表达式编程

GEP的编码方式是长度固定的线性符号串，称为GEP染色体。一个染色体包含一个或多个基因。每个基因由头部和尾部组成，头部允许出现终结符和函数符号，尾部只能出现终结符。

头部的长度h是事先设定的，而尾部的长度t则由以下公式计算得到

式中：n——所使用的函数集中需要参数最多的函数的参数个数。假设符号集为 ｛＋，－，＊，＼｝，则n＝2。设h＝3，则尾部长度t＝4。于是，

GEP基因的基因型是K表达式（K－expression），表现型为表达式树（expression tree）。两者之间可以相互转换。

K表达式解码为表达式树的方法是：按从左到右的顺序逐一读取基因中的字符，然后根据语法规则按照层次顺序从上到下，从左到右排放即可。反之，对表达式树按照从上到下，从左到右的顺序遍历，即可得到对应的K表达式。

以基因（2）为例，其对应的表达式树如图1所示，其对应的K表达式是

其对应的数学公式是

图1 基因（2）对应的表达式树

显然，GEP基因的K表达式是编码部分从头开始的有效部分，尾部的符号不一定全部有用。如基因（2）尾部最后的两个符号“bb”并没有出现在K表达式中。

而对于如下基因

其对应的表达式树如图2所示，它表示的数学公式是

对应的K表达式是

在这里，基因编码的所有符号都出现在K表达式中。

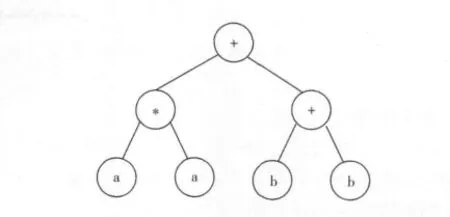
图2 基因（5）对应的表达式树

1.1 基于小生境技术的GEP

演化算法师法自然，模拟自然界的生物演化过程。但在实际的演化算法设计过程中，群体的规模一般只有几十或几百，这个数字与生物界的物种规模相差甚远。另外，演化算法的杂交和变异是随机的，这种随机性在演化初期能够保持解的多样性，但在演化后期，如果出现了“超级个体”，该个体可能很快就会得到大量繁殖，导致算法过早地收敛到一个局部最优点，这种现象称为过早收敛（早熟收敛）。作为演化算法的一种，传统的GEP同样具有容易陷入局部最优的缺陷。

为了保持群体的多样性，提高算法的全局寻优能力和收敛速度，小生境理论被广泛应用到演化算法中。

小生境的基本思想来源于自然界中，特征、形状相似的物种往往聚在一起，并与同类交配繁衍后代。反映到演化算法中就是要让算法中的个体在一个特定的生存环境中进化。基于小生境的演化算法，把种群划分为若干小生境，每个小生境就是具有相似适应值的个体的集合。然后在小生境内部以及小生境之间，通过杂交、变异产生新一代群体，然后采用预选择（preselection）机制、排挤（crowding）机制或分享（sharing）机制完成对种群的选择操作。

小生境技术主要是对演化算法中常规的选择策略进行改进。基于预选择机制的选择策略，其基本做法是：只有当新产生的子代个体的适应度超过其父代个体的适应度时，该子代才能代替其父代而遗传到下一代群体中去，否则保留父代个体。由于子代个体与父代个体相似，所以替换掉的是结构相似的个体，从而能维持种群的多样性。

清除（Clearing）算法类似于适应值共享，它需要的参数包括小生境半径σ和小生境的容量χ。算法先对群体中的个体按适应值降序排列。然后对种群中的每个个体逐一进行判断：如果个体i的适应值大于0并且它和所有小生境中心的距离都大于σ，那么以该个体为中心形成新的小生境；如果个体i到某个小生境中心的距离小于σ，并且该小生境中的个体数量小于χ，那么该个体被添加到该小生境中，该小生境中的个体数量加l；不满足以上条件的个体，其适应值被设置为0。

文献［10］将小生境概念引入到GEP中，实现用GEP进行多模函数优化。文献［11］在GEP中采用改进的k－均值的聚类分析，保持群体多样性，提高算法跳出局部最优的能力。但是算法需要对种群个体进行排序，增加了算法复杂度。

1.2 多样性的测度

生物学中的多样性是指种群中个体的不同，包括个体结构和行为的差异。在演化算法中，种群的多样性往往指基因结构的差异，或者是适应值的差异。

本文采用多基因的染色体，多基因之间用加法连接，基因的顺序对整个染色体的适应值没有影响。因此，不便于用基因结构来描述其差异，而是直接采用适应值的不同来描述种群多样性。

定义1 假定种群规模为N，第t代的种群中不同个体的数目记为n（t），种群的多样度记为

显然，0＜D（t）≤1，D（t）越大，则群体的多样性就越丰富。

2 基于改进小生境技术的GEP

文献［2］以挖掘函数f（n）＝5n4＋4n3＋3n2＋2n＋1为例，分析了不同遗传算子对种群多样性的影响，并指出：重组算子（包括基因交换、单点杂交和两点杂交）容易产生大量相同个体并最终导致种群完全失去多样性，因此常常容易出现过早收敛的现象。

基于小生境的GEP新算法niche－GEP，采用类似于清除算法的小生境技术，其参数包括小生境半径σ和小生境容量x。小生境半径σ设置为0，即相同适应值的个体组成一个小生境；小生境容量x限定了适应值相同的个体的数量上限，避免出现大量重复个体。需要说明的是，具有相同编码的个体，它们的适应值一定是相等的；但具有相同适应值的个体，它们的编码不一定相同。

清除算法需要对种群按适应值大小进行降序排序，以保证每个小生境的中心是该小生境中适应值最大的个体，同时也保证淘汰掉的是相似个体中适应值较小的个体。但是排序也增加了算法的计算量。

niche－GEP算法不需要进行排序。因为所有不同适应值的个体都得以保留，即使是适应值相似的个体。当相同适应值的个体数量超过小生境容量x时，超过的个体被初始化。在演化算法中，初始化部分个体是增加种群多样性的有效方法之一。这些被重新初始化的个体，增加了种群的多样性，也许其适应值很小，但是有可能包含良好的基因片段，在经过杂交、变异后，产生优良个体。

改进的小生境算法描述如下：

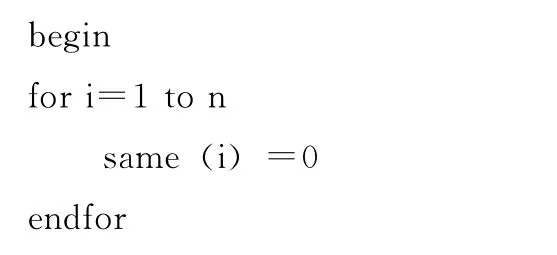
其中，x为小生境容量，same（i）表示与个体i适应值相同的个体的数量，fitness（i）表示个体i的适应值，initialize（i）表示初始化个体i。

niche－GEP算法框架如下：

步骤1 初始化种群并计算种群中所有个体的适应值。

步骤2 对种群中的个体进行变异、重组等遗传操作，产生后代。当后代个体的适应值大于父代个体的适应值时，取代父代个体，否则保留父代个体。

步骤3 通过小生境技术初始化部分重复个体。

步骤4 如果达到设定的最大演化代数，则结束运行，否则转到步骤2。

3 仿真试验及分析

分别对一元函数和二元函数进行试验，小生境容量x＝3，GEP相关参数的设置见表1。

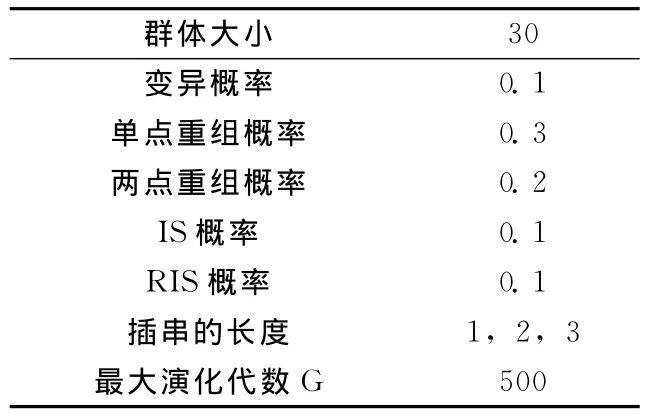
表1 参数设置

3.1 实验1

实验1模拟以下一元函数的挖掘过程

根据这个公式，产生10组训练数据，见表2。

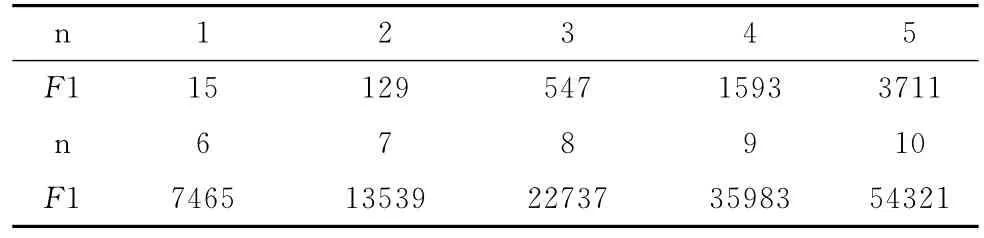
表2 挖掘函数F1所用的训练数据

基因头部长度为6，一个染色中包含的基因个数为4，其它参数的设置如表1所示。算法连续运行100次，取平均值为统计结果。从种群多样性、成功率和收敛速度三方面，对GEP和niche－GEP进行比较。演化过程中种群多样性的变化如图3所示；算法成功率的比较如图4所示；算法收敛时的平均代数如图5所示。

实验数据表明，在挖掘F1函数时，niche－GEP在种群多样性、算法成功率和收敛速度3方面都优于传统GEP。

3.2 实验2

实验2模拟挖掘二元函数

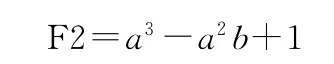
根据这个公式，随机产生10组范围在［－10，10］的数据作为训练数据。基因头部长度为4，一个染色中包含的基因个数为3，其它参数的设置如表1所示。算法连续运行100次，种群多样性的变化如图6所示；算法成功率的比较如图7所示；算法收敛时的平均代数的比较如图8所示。

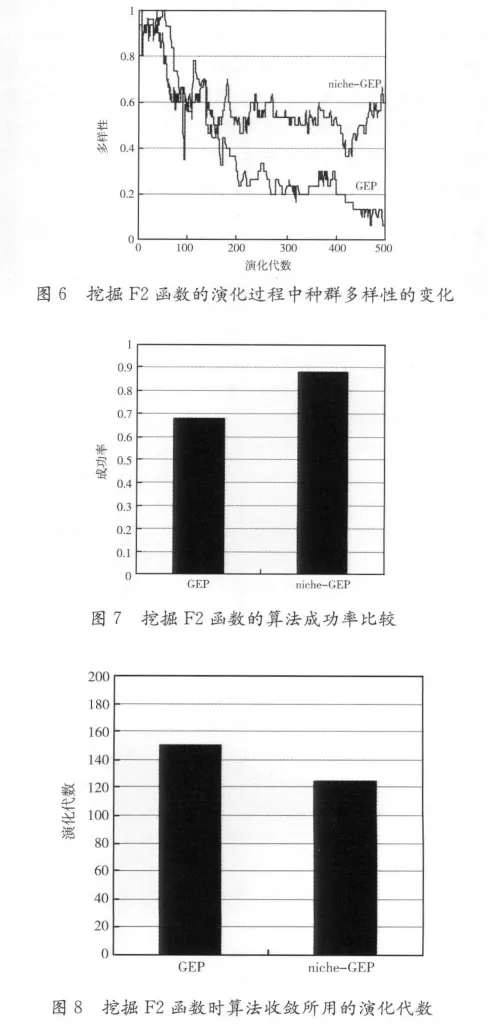
在挖掘函数F2时，niche－GEP的成功率优于GEP，在收敛速度方面也有一定提高。从图3和图6看出，在演化进行到200代以前，GEP和niche－GEP的多样性都比较丰富，niche－GEP并没有优势。但在200代以后，GEP的多样性明显下降，容易陷入局部最优。niche－GEP由于始终保持较丰富的多样性，能从总体上提高算法的成功率。

4 结束语

由于GEP中的重组算子容易产生大量重复个体，使种群中的个体趋向于一致，群体的多样性缺失，导致算法容易陷入局部最优而出现早熟现象。鉴此，提出了一种基于小生境的GEP新算法，该算法将相同适应值的个体组成一个小生境，如果相同适应值的个体数量超过小生境容量x，则将超出的个体放入演化池中进行重新初始化。并分别对一元函数和二元函数进行模拟挖掘。实验表明，新算法能在整个演化过程中保持丰富的群体多样性，能够有效地避免算法的早熟现象，在算法成功率和收敛速度方面都优于传统的GEP算法。

［1］XIANG Yong，TANG Chang－jie，ZHU Ming－fang，et al.Embedded gene expression programming and its application in function mining［J］.Journal of University of Electronic Science and Technology of China，2011，40（1）：116－121（in Chinese）.［向勇，唐常杰，朱明放，等.内嵌基因表达式编程及其在函数发现中的应用［J］.电子科技大学学报，2011，40（1）：116－121.］

［2］MO Hai－fang，KANG Li－shan.Automatic modeling of complex functions based on gene expression programming［J］.Journal of System Simulation，2008，20（11）：2828－2831（in Chinese）.［莫海芳，康立山.用GEP实现复杂函数的自动建模［J］.系统仿真学报，2008，20（11）：2828－2831.］

［3］MO Hai－fang，LI Kang－shun.New genetic operator of gene expression programming［J］.Computer Engineering and Applications，2011，47（7）：23－25（in Chinese）.［莫海芳，李康顺.基因表达式编程的一种新遗传算子［J］.计算机工程与应用，2011，47（7）：23－25.］

［4］QI Xing，QIN xu－jia，LI Qu.An improved method for evolving GEP neural network［J］.Computer Systems＆ Applications，2009，19（4）：49－52（in Chinese）.［齐星，秦绪佳，李曲.一种改进的GEP神经网络演化方法及其应用［J］.计算机系统应用，2009，19（4）：49－52.］

［5］WANG Wei－hong，RUAN Wei，LI Qu.Decision tree algorithm by gene expression programming based on differential evolution［J］.Computer Engineering，2011，37（1）：181－183（in Chinese）.［王卫红，阮薇，李曲.基于差分演化的GEP决策树算法［J］.计算机工程，2011，37（1）：181－183.］

［6］WU Zhi－jian，JIANG Da－zhi，TANG Ming－duan.New algorithm based on gene expression programming［J］.Journal of System Simulation，2008，20（8）：1986－1989（in Chinese）.［吴志健，姜大志，汤铭端.一种基于基因表达式程序设计的新算法［J］.系统仿真学报，2008，20（8）：1986－1989.］

［7］ HU Jian－jun，TANG Chang－jie，DUAN Lei，et al.The strategy for diversifying initial population of gene expression programming［J］.Chinese Journal of Computers，2007，30（2）：305－309（in Chinese）.［胡建军，唐常杰，段磊，等.基因表达式编程初始种群的多样化策略［J］.计算机学报，2007，30（2）：305－309.］

［8］LI Tai－yong，TANG Chang－jie，WU Jiang，et al.Adaptive population diversity tuning algorithm for gene expression programming［J］.Journal of University of Electronic Science and Technology of China，2010，39（2）：279－283（in Chinese）.［李太勇，唐常杰，吴江，等.基因表达式编程种群多样性自适应调控算法［J］.电子科技大学学报，2010，39（2）：279－283.］

［9］ HU Jian－jun，TANG Chang－jie，PENG Jing.VPS－GEP：Skipping from local optimization fast algorithm［J］.Journal of Sichuan University（Engineering Science Edition），2007，39（1）：128－133（in Chinese）.［胡建军，唐常杰，彭京，等.快速跳出局部最优的VPS－GEP算法［J］.四川大学学报（工程科学版）.2007，39（1）：128－133.］

［10］LI Tai－yong，TANG Chang－jie，WU Jiang.Multimodal function optimization based on niche gene expression programming［J］.Journal of Sichuan University（Engineering Science Edition），2009，41（2）：162－166（in Chinese）.［李太勇，唐常杰，吴江.等.基于小生境基因表达式编程的多模函数优化［J］.四川大学学报（工程科学版），2009，41（2）：162－166.］

［11］LIN Yi－shen，PENG Hong，WEI Jia.Function finding in niching gene expression programming［J］.Journal of Chinese Computer Systems，2008，29（11）：2111－2114（in Chinese）.［林毅申，彭宏，韦佳.小生境基因表达式编程在函数发现的研究［J］.小型微型计算机系统.2008，29（11）：2111－2114.］