自适应视野和步长的局部邻域人工鱼群算法
2012-07-27许恒迎孙伟斌牛慧娟白成林
许恒迎,孙伟斌,张 霞,牛慧娟,白成林+
(1.聊城大学 物理科学与信息工程学院,山东 聊城252000;2.山东省光通信科学与技术重点实验室,山东 聊城252000)
0 引 言
人工鱼群算法(AFSA)是李晓磊博士提出的一种基于行为的新型人工智能算法[1],通过模拟鱼群的觅食、聚群、追尾、随机等行为实现全局寻优,具有鲁棒性强、全局收敛性好以及对初值选择不敏感等特点,目前在传感器网络优化、水质参数识别、多用户检测器、参数优化、路由选择及组合优化等多个工程领域已得到应用并取得了良好效果[2-6]。许多研究学者针对人工鱼群算法在运行后期表现出的搜索盲目性较大、寻优精度低、对于复杂问题易陷入局部极值等缺陷做出了改进,如张梅凤等提出了基于生境的人工鱼群算法,较好解决了多峰问题,但步骤比较繁琐[7];刘彦君通过自适应地改变人工鱼的视野和步长提高了寻优精度,但是易陷入局部极值[8];王联国提出了全局版人工鱼群算法,提高了运算速度,但目标的寻优精度有待提高[9]。在这些学者研究成果的基础上,针对AFSA寻优精度差、易陷入局部极值和过早收敛的问题,本文提出了一种采用自适应视野和步长的局部邻域人工鱼群算法(local neighborhood artificial fish swarm algorithm,LNAFSA)。该算法采用了一种全新的局部邻域结构,每条人工鱼只能与本邻域结构内的其他5条邻居鱼相互交换信息。每次迭代前每条人工鱼都要根据自身与其他5条邻居鱼的距离自适应地计算视野和步长,增强了鱼群个体之间的差异性,简化了参数设定。在聚群行为中每条人工鱼计算所在邻域结构的中心,减少了求视野范围内人工鱼之间距离的计算量,追尾行为中则跟踪所在邻域结构内的最优人工鱼,由于采用了这种固定的邻域结构而无需判断视野范围内哪条人工鱼才是邻居,算法迭代速度得以提高。经6个经典测试函数和1个光纤通信系统偏振模色散(PMD)补偿的工程实例验证,表明该算法的寻优精度和迭代速度均得到了较大改善,有效抑制了过早收敛现象。
1 基于自适应视野和步长的局部邻域结构人工鱼群算法
1.1 全新的局部邻域结构
在AFSA中,假设第i条人工鱼的状态表示为向量Xi=(x1,x2,…,xn),它的感知距离为Visual,移动的步长为Step,拥挤度因子为δ,第i条人工鱼对应的食物浓度为Y=f(Xi),任意两条人工鱼i、j之间的距离定义为di,j=‖Xi-Xj‖,则第i条人工鱼的邻域定义为N={Xj|di,j<Visual},邻居人工鱼的数目为nf[1]。
文献[1]指出人工鱼的数目越多,收敛速度越快,但是迭代计算量越大,综合考虑以上因素及测试函数的要求,人工鱼的总数设定为20。受文献[10]的启发,我们使用模拟退火算法随机地改变这20条人工鱼之间的连接,并且将邻居鱼数目从1逐渐增加到10,这样可以得到1300余种可能的局部邻域结构。采用Sphere、Rastrigin、Griewank、Rosernbrock、f6等5个经典测试函数测试并比较所有局部邻域结构的性能,发现邻居鱼数目为5时所需迭代次数最少并且迭代成功率可达到95%以上。图1给出了LNAFSA算法采用的一种具有5条邻居鱼并且迭代成功率可以达到100%的邻域结构拓扑图。在该结构中,每条人工鱼的生存环境位于6条人工鱼(包含自身和5条邻居人工鱼)组成的空间结构中,每条人工鱼只能与其邻居人工鱼交换信息。
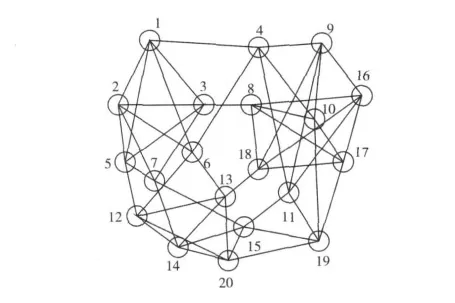
图1 全新局部邻域结构的拓扑
图1中每个圆圈代表一条人工鱼,圆圈外的数字代表每条人工鱼的编号,连线表示相连人工鱼可以相互交换信息。这种邻域结构中每条人工鱼的生存环境可用表1表示。

表1 每条人工鱼的局部邻域结构
1.2 自适应视野和步长
在AFSA中,所有人工鱼的视野Visual和步长Step都是事先设定的固定值。这是两个非常重要的参数,直接决定了寻优结果的精度。如果视野和步长较大,人工鱼全局搜索能力强并能快速收敛,但在收敛后期不可避免的出现人工鱼在最优值附近来回振荡的现象;如果视野和步长较小,人工鱼收敛速度变慢,可以提高收敛精度,但在局部极值突出的情况下,很容易陷入局部极值而难以逃离。因此,有必要使视野和步长随着迭代的进行能够自适应地调整。
现在每条人工鱼已处于表1所示的局部邻域结构中,每次迭代前,第i条人工鱼均要计算与其他5条邻居人工鱼的距离,取平均值后乘以限制因子K1及函数α(t)后再加上视野常量Visualmin,作为该人工鱼当前的自适应视野Visuali;将Visuali乘以1/8及α(t)后再加上步长常量Stepmin,作为该人工鱼当前的自适应步长Stepi。计算公式为
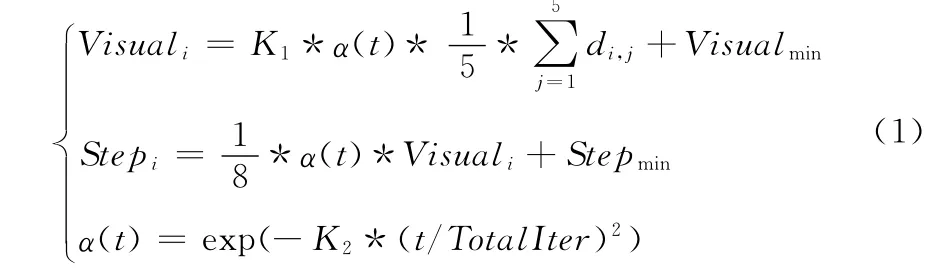
式(1)中,限制因子K1是在0~1之间的常数,它的取值与函数自变量搜索的范围及维数有关。α(t)决定了视野、步长与迭代次数的变化关系[11]。Visualmin和Stepmin的主要作用是防止算法在运行后期与其他5条邻居人工鱼的平均距离无限接近0时出现停止收敛的现象。α(t)中K2为限制因子,TotalIter是一迭代总次数常量,因此α(t)是一个随迭代次数t的增大而逐渐减小的函数。
1.3 基于局部邻域结构的人工鱼行为描述
1.3.1 聚群行为
假设当前时刻第i条人工鱼的状态为Xi=(x1,x2,…,xn),且第i条人工鱼所在邻域结构的中心位置Centeri=(center1,center2,…centerk,…,centern),每一分量centerk的计算公式为

式中:m——第i条人工鱼邻域结构的每条邻居人工鱼,AFNeighbori——第i条人工鱼所在的邻域结构(包括自身)。假设中心位置Xc对应的食物浓度Yc=f(Xc),如果Yc/nf>δ*Yi(对应求极大问题,极小问题为 Yc/nf<δ*Yi),说明Centeri处食物浓度更高且可容纳下自身,则第i条人工鱼朝Centeri位置前进一步,下一时刻位置分量xinextk按式(3)计算,否则根据下文所述的行为选择策略执行追尾或觅食行为
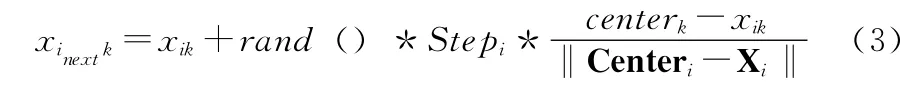
式中:rand()—— 一个0到1之间的随机实数,Stepi——当前迭代第i条人工鱼的步长。
1.3.2 追尾行为
遍历第i条人工鱼所处的局部邻域结构,找到本邻域内最优人工鱼,假设其状态为AFlocalbest,这条最优人工鱼对应的食物浓度为Localbest。如果Localbest/nf>δ*Yi(对应求极大问题,极小问题为Localbest/nf<δ*Yi),说明邻域内的最优人工鱼AFlocalbest处更优且可容纳下自身,则第i条人工鱼朝AFlocalbest的方向前进一步,下一时刻位置分量xinextk按式(4)计算,否则根据下文所述的行为选择策略执行聚群或觅食行为
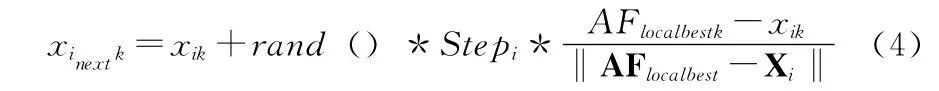
式中:AFlocalbestk——第i条人工鱼所在局部邻域内最优人工鱼对应的位置分量。
1.3.3 觅食行为
当前迭代第i条人工鱼的视野为Visuali,则第i条人工鱼在[-Visuali,Visuali]范围内随机巡视得到一个状态Xrand,设定此状态下的食物浓度为Yrand。如果它们各自对应的食物浓度Yrand>Yi(对应求极大问题,极小问题为Yrand<Yi),为加快寻优速度,第i条人工鱼直接移动到该位置。若将以上过程尝试进行了try_number次后仍未发现更高的食物浓度,则第i条人工鱼在[-Stepi,Stepi]范围内随机选择一值作为下一时刻游动时的位置增量。
1.3.4 行为选择
因人工鱼的行为种类较多,下一时刻具体执行哪种行为需依据具体处理问题的不同而选择不同的行为选择策略。本文采用的是进步即可原则[11],即首先执行聚群行为,若未发现更高食物浓度则执行觅食行为,如果仍未发现更优值则执行追尾行为,最后若依然未发现更高食物浓度则执行觅食行为。
1.3.5 公告板
在寻优过程中,每条人工鱼每次行为(如聚群、觅食、追尾或随机行为)完毕就将自身状态与公告板的状态进行比较,优则替换公告板上的记录。最后,算法根据公告板的记录得到最终的寻优结果。
1.3.6 算法流程
步骤1 设定人工鱼群规模、每条人工鱼所在的局部邻域结构AFNeighbor、拥挤度δ、觅食行为中重复尝试次数try_number、限制因子K1和K2、最大迭代次数等参数。
步骤2 在搜索空间内随机初始化每条人工鱼的位置,计算此时每条人工鱼的食物浓度(即对应的函数值),并与公告板的状态比较,优则替换。
步骤3 根据式(1)自适应调整此次迭代每条人工鱼的视野和步长。
步骤4 每条人工鱼在局部邻域结构内按照上述进步即可原则执行各种行为,每条人工鱼的位置和公告板状态也随之进行更新。
步骤5 判断迭代次数是否达到预定最大迭代次数或寻找到的最优值是否满足精度要求。若条件满足,则输出最优值,算法终止;否则返回步骤3,继续下一次迭代。
2 收敛分析
一种算法具备全局收敛性的充要条件是:
(1)具备局部收敛性;
(2)提供从局部最优解状态向其他未被搜索空间转移的方法;
(3)提供搜索整个状态空间的策略[12]。以下讨论LNAFSA算法满足这样3个条件:
对于条件(1):第i条人工鱼在执行聚群或追尾行为时,如果在AFNeighbori的中心位置或在AFNeighbori内最优人工鱼处发现更优值并且不太拥挤,则朝其前进一步,这种策略可以保证经过一定次数的迭代后第i条人工鱼在本邻域内找到局部最优值,显然具备局部收敛性。如果第i条人工鱼执行觅食行为,由觅食行为的定义可知,第i条人工鱼总要朝更优方向前进,保证了局部收敛。因此,满足条件(1)。
对于条件(2):每条人工鱼的生存环境位于自身和5条邻居人工鱼组成的局部邻域结构中,每条人工鱼只能与其邻域交换信息。这种全新的局部邻域结构可以有效提升人工鱼群算法的性能。如果某条人工鱼陷入了局部极值,影响的范围也仅仅是本邻域结构,可以依靠本邻域内其它5条人工鱼发现的更优值吸引其快速“逃离”陷入的局部极值,向其他未被搜索的空间游动。如果某条人工鱼发现了更优值,既可以直接将这一信息与本邻域内的其余5条人工鱼分享,又可以通过邻域结构的重叠性逐渐传播到整个群体。因此,LNAFSA算法采用的这种局部邻域结构既具有局部性又具有全局性,满足条件(2)。
对于条件(3):LNAFSA算法初始化时,所有人工鱼随机地均匀分布在函数的搜索空间中,对应局部邻域结构内与其他5条人工鱼的距离平均值较大,按照式(1)每条人工鱼均具有较大的视野和步长,可以搜索整个状态空间,从而加强了全局搜索能力。随着迭代次数的增加,每条人工鱼都有向最优值方向游动的趋势,对应所在邻域内与其他5条人工鱼的平均距离逐渐减小,按式(1)逐渐减小它的视野和步长。在迭代后期,当人工鱼游动至最优值附近时,其视野和步长将降低至非常小便于实现局部区域的精细搜索。每次迭代时每条人工鱼通过平均距离计算得到的视野和步长均不同,赋予了人工鱼更多的智能。因此,这种方法实现了视野和步长的自适应调整,兼顾了收敛速度和寻优精度,在加强局部搜索能力的同时又提高了目标精度,满足条件(3)。
因此,LNAFSA算法具备全局收敛性。
3 实验结果分析
3.1 实验设计
在Matlab R2006b环境下,机器主频为Intel Core2 2GHz,内存为1GB。选取6个经典测试函数进行实验:
(5)Rotated hyper-ellipsoid Function:f5(x)=,它是一个病态的高维单峰函数,在xi=0i=1,2,…n时达到全局最小值,最优值为0。
3.2 实验结果及分析
人工鱼群规模为20,觅食行为中重复尝试次数try_number=5。其余参数设置见表2。
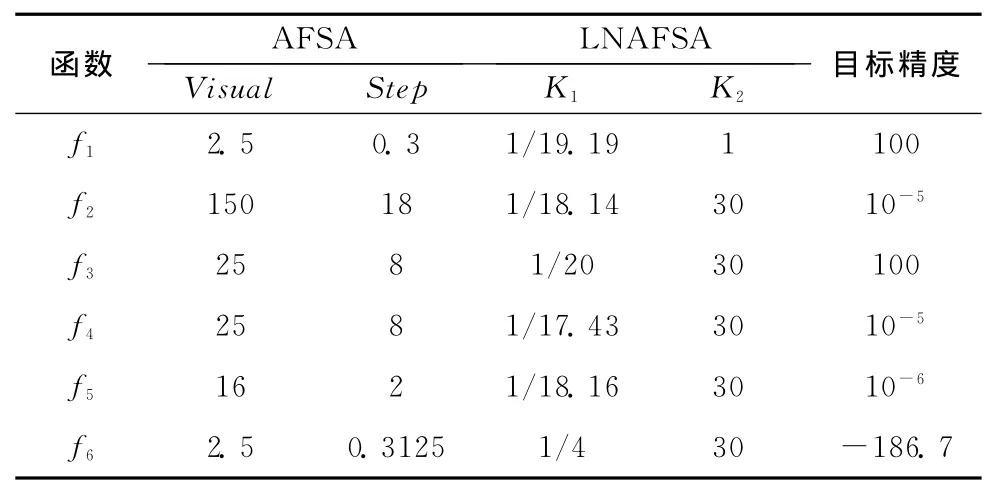
表2 算法的参数设置
设定f1~f4的维数均为30维,f5为5维,f6为2维,对于每一测试函数算法均独立运行50次,其中每次迭代循环2000次,记录这50次运行所得结果的最好值、最劣值、均值、标准差、达到目标精度时所用的最大、最小及平均迭代次数以及每次迭代的平均运行时间,以这些数据作为衡量算法性能的指标[8-9,11,14]。实验结果如表3和图2~图7所示。
表3中“—”表示迭代次数超过了最大迭代次数2000,意味着算法寻优的最终结果没有达到规定的目标精度[9,14]。由表3可以看出,LNAFSA的寻优结果明显好于AFSA,并且这种算法的稳定性更好。以表2规定的目标优化精度作为衡量指标,由测试结果可知:AFSA对于函数f650次内有27次优化至目标精度内,具有一定的优化能力,对于函数f1~f5则完全不能优化;而LNAFSA对6个测试函数均能寻优至目标精度内,都成功实现了优化,平均迭代次数最多是1194次,并且它的平均运行时间更短,大约为AFSA的1/3。
图2~图7是分别采用LNAFSA和AFSA对函数f1~f6运行50次后得到的每次迭代平均最优值的进化曲线。为方便对比,f1~f5的全局最优值分别取自然对数,f6每次的寻优结果均为负值,故图7采用了f6每次迭代后的全局最优值。从图2~图7可以看出,LNAFSA具有很强的克服局部极值的能力,收敛速度快,寻优精度更高,明显优于AFSA。

表3 AFSA与LNAFSA算法优化结果
3.3 与参考文献中改进算法的优化性能比较
选取文献[9,13,14]共有的测试函数f1与f3,设定f1与f3的维数分别为10、20和30,相应迭代循环次数分别设置为1000次、1500次和2000次,LNAFSA在f110维时K1取1/10,20维时K1取1/15,对于f310维和20维的K1均取1/20,其他参数同上。每个函数进行50次实验,取全局最优值的平均值,与文献[13]中改进型粒子群算法优化结果、文献[9]全局版人工鱼群算法及文献[14]基于冯诺依曼结构的人工鱼群算法结果进行比较,实验结果见表4。
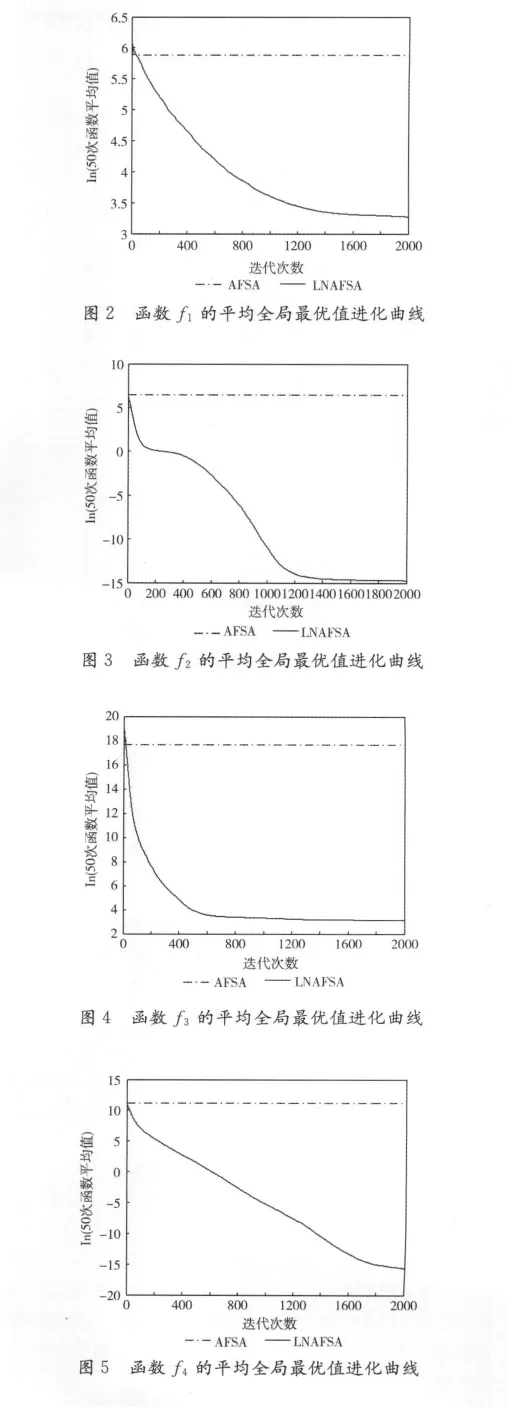
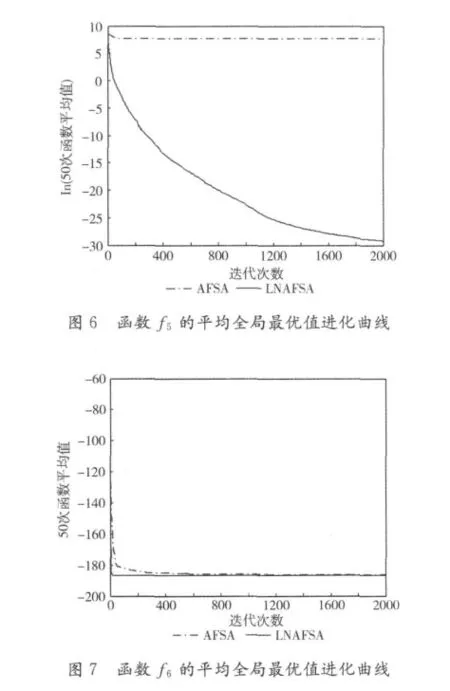
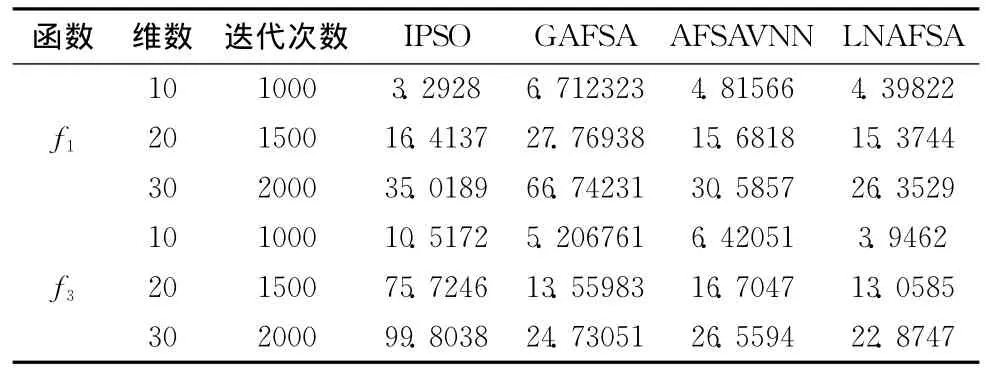
表4 与参考文献中改进算法的优化结果比较
通过表4可以看出,LNAFSA对于函数f1和f3的优化结果全面优于IPSO、GAFSA和AFSAVNN。因此,这种算法的优化性能更好。
3.4 实例测试
本文利用LNAFSA进行40Gb/s光纤通信系统二阶偏振模色散(PMD)补偿,并与文献[15]中应用单纯形算法和遗传算法的结果进行了比较,进一步检验算法的优化性能。
LNAFSA的参数设置为视野最小值Visualmin=0.001,步长最小值Stepmin=0.0002,重复尝试次数try_number=5,拥挤度因子δ=0.5,最大迭代次数TotalIter=50。该实例测试以光纤链路偏振度(DOP)作为目标函数值,理论上完全进行二阶PMD补偿后DOP值应为1,测试结果见表5。
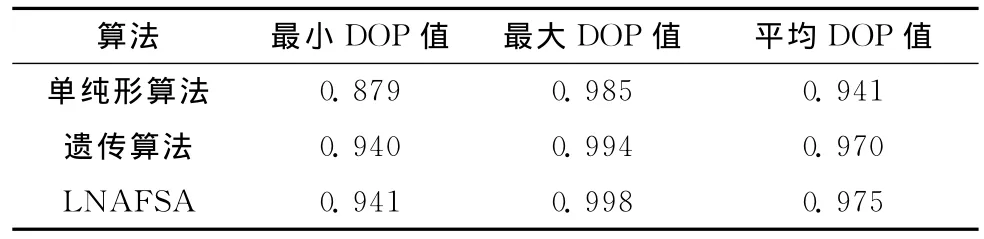
表5 与单纯形算法和遗传算法的二阶PMD补偿结果比较
由表5可以看出,LNAFSA得到的最小、最大和平均目标函数值均优于单纯形算法和遗传算法,该算法可有效解决此类工程问题。
4 结束语
针对AFSA寻优精度差、易陷入局部极值和过早收敛的问题,提出了基于自适应视野和步长的局部邻域人工鱼群算法。该算法具有两个主要的优点:一是采用了全新的局部邻域结构,使得人工鱼能够快速逃离局部极值,克服了基本人工鱼群算法容易过早收敛的缺陷,提高了算法的全局寻优能力;二是每条人工鱼采用了基于本邻域结构内平均距离的自适应视野和步长,达到了视野和步长自适应调整的目的,使算法具备了更多的人工智能,实现了收敛速度和寻优精度的双赢。仿真结果表明,这是一种简单、高效的人工鱼群算法。
[1]LI Xiao-lei,LU Fei,TIAN Guo-hui,et al.Applications of artificial fish school algorithm in combinatorial optimization problems[J].Journal of Shandong University:Engineering Science,2004,34(5):64-67(in Chinese).[李晓磊,路飞,田国会,等.组合优化问题的人工鱼群算法应用[J].山东大学学报,2004,34(5):64-67.]
[2]LIAO Can-xing,ZHANG Ping,LI Xing-shan,et al.Optimal deployment in sensor networks based on hybrid artificial fish school algorithm[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(3):373-377(in Chinese).[廖灿星,张平,李行善,等.基于混合人工鱼群算法的传感器网络优化[J].北京航空航天大学学报,2010,36(3):373-377.]
[3]GAO Yufang,CHEN Yaodeng.The optimization of water utilization based on artificial fish-swarm algorithm[C].Yantai:Sixth International Conference on Natural Computation,2010:4415.
[4]YU Yang,YIN Zhi-feng,TIAN Ya-fei.Multiuser detector based on adaptive artificial fish school algorithm[J].Journal of Electronics & Information Technology,2007,29(1):121-124(in Chinese).[俞洋,殷志锋,田亚菲.基于自适应人工鱼群算法的多用户检测器[J].电子与信息学报,2007,29(1):121-124.]
[5]BAN Xiao-juan,YANG Yun-mei,NING Shu-rong,et al.A self-adaptive control algorithm of the artificial fish formation[C].Korea:IEEE International Conference on Fuzzy systems,2009:1903-1908.
[6] WANG Xing-wei,QIN Pei-yu, HUANG Min.ABC supporting QoS unicast routing scheme based on the artificial fish swarm[J].Chinese Journal of Computers,2010,33(4):718-725(in Chinese).[王兴伟,秦培玉,黄敏.基于人工鱼群的ABC支持型QoS单播路由机制[J].计算机学报,2010,33(4):718-725.]
[7]ZHANG Mei-feng,SHAO Cheng.Niche artificial fish swarm algorithm for multimodai function optimization[J].Control Theory & Applications,2008,25(4):773-776(in Chinese).[张梅凤,邵诚.多峰函数优化的生境人工鱼群算法[J].控制理论与应用,2008,25(4):773-776.]
[8]LIU Yan-jun,JIANG Ming-yan.Improved artificial fish swarm algorithm based on adaptive visual and step length[J].Computer Engineering and Applications,2009,45(25):35-47(in Chinese).[刘彦君,江铭炎.自适应视野和步长的改进人工鱼群算法[J].计算机工程与应用,2009,45(25):35-47.]
[9]WANG Lian-guo,HONG Yi,SHI Qiu-hong.Global edition artificial fish swarm algorithm[J].Journal of System Simulation,2009,21(23):7483-7502(in Chinese).[王联国,洪毅,施秋红.全局版人工鱼群算法[J].系统仿真学报,2009,21(23):7483-7502.]
[10]James Kennedy,Rui Mendes.Neighborhood topologies in fully informed and best-of-neighborhood particle swarms[J].IEEE Trans on Systems,Man,and Cybernetics,Part C:Applications and Reviews,2006,36(4):515-519.
[11]WANG Lian-guo,HONG Yi,ZHAO Fu-qing,et al.Improved artificial fish swarm algorithm[J].Computer Engineering,2008,34(19):192-194(in Chinese).[王联国,洪毅,赵付青,等.一种改进的人工鱼群算法[J].计算机工程,2008,34(19):192-194.]
[12]ZHU Xi-lu,WANG Bai.Niche genetic algorithm based on cluster division[J].Control and Decision,2010,25(7):1113-1116(in Chinese).[祝希路,王柏.一种基于社团划分的小生境遗传算法[J].控制与决策,2010,25(7):1113-1116.]
[13]JIANG Yan,HU Tie-song,HUANG Chong-chao,et al.An improved particle swarm optimization algorithm[J].Applied Mathematics and Computation,2007,193(1):231-239.
[14]WANG Lian-guo,HONG Yi.Artificial fish-swarm algorithm based on Von Neuman neighborhood[J].Control Theory &Applications,2010,27(6):775-780(in Chinese).[王联国,洪毅.基于冯·诺依曼邻域结构的人工鱼群算法[J].控制理论与应用,2010,27(6):775-780.]
[15]WANG Xian-qing,WANG Hong-xiang,JI Yue-feng,et al.Control Algorithms In Adaptive PMD Compensation System[J].Journal of Beijing University of Posts and Telecommunications,2007,30(1):110-113(in Chinese).[王先庆,王洪祥,纪越峰,等.自适应偏振模色散补偿系统中的控制算法[J].北京邮电大学学报,2007,30(1):110-113.]
