H65黄铜管冷轧变形模拟分析与实验研究

周玉雄,林高用, 雷玉霞,王 宏,张胜华

(1.中南大学材料科学与工程学院，湖南 长沙 410083)(2. 江苏太仓市金鑫铜管有限公司，江苏 苏州 215412)

传统的铜管生产方式主要采用 “实心锭—穿孔挤压—(冷轧)—拉伸”法，即“挤压法”。“挤压法”无法生产大长度的管材，且挤压时穿孔料头、挤压脱皮、压余等工艺废料通常占到锭坯重量的20-30%，因此“挤压法”生产铜管成品率较低，该方法现在逐渐受到新型的高效短流程铜管生产技术的挑战。目前铜管加工的新技术有水平连铸空心锭坯-行星轧制”法，即“铸轧法”，该技术已成功应用于紫铜和白铜管的大量生产，然而对于H65等普通黄铜来说却未能实现，这是因为行星轧制的温升过高(高达700℃)，而黄铜在200℃～700℃会发生脆性转变，轧制易出现开裂现象。国内部分企业正在尝试采用另外一种无挤压的高效短流程铜管加工技术，即“水平连铸管坯—皮尔格冷轧开坯—拉拔”法进行黄铜管生产， 采用该技术已能成功生产紫铜管和α单相黄铜管，但对于H65黄铜管的加工尚存在一定的困难。H65有较宽的主成份范围，属于介于α单相和α+β黄铜的一种合金，其加工工艺较难把握。采用冷轧方式开坯时，若工艺控制不当，管坯中的温升仍可能引发β′，脆性相的析出，加上冷轧时不均匀变形严重，两轧辊间开口部位的管坯将承受较大附加拉应力，于是冷轧时容易产生表面裂纹[1-4]。目前，除了本文作者外，对H65黄铜的冷轧开坯工艺尚无任何报导。

本文结合生产试验，采用有限元数值模拟技术对H65黄铜管冷轧变形开展深入分析，研究成形过程中的温度和附加应力分布，由此为工艺优化提供依据。

1 有限元建模

1.1 模型简化

皮尔格冷轧管是一小段 m长的管坯在由孔型和芯棒所构成的、尺寸逐渐减少的环形间隙中进行减径和减壁厚的过程。整个过程是周期性、高度非稳态的过程，每一小段m长的管坯轧制到成品管尺寸都必须经历十几次到几十次的辗轧周期，每个周期又由正行程、反行程、管料送进和旋转部分(如图1所示，旋转角度θ不能是360°/n，以避免回转角的耦合)组成,且进程轧制又分为减径段、压下段、预精整段和精整段。因此，任何完全预测的从头计算的有限元模拟是不现实的。为此对模型做如下简化[5]：

(1)对于单送进单回转的皮尔格冷轧管，由于反行程轧制时管料的变形主要是弹性变形，因此，本文将忽略反行程轧制，只模拟一个正行程的轧制过程；

(3)由于整个冷轧管过程变形主要发生在减径段和压下段，故只对减径段和压下段进行建模和分析，且工作段管坯的几何模型是结合轧辊孔型和芯棒建立的。

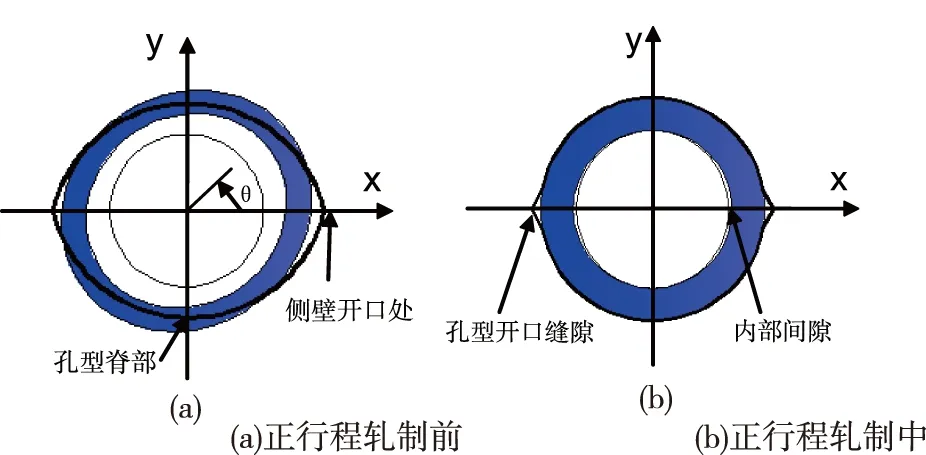
图1 特定Z坐标下的管坯(阴影部分)和孔型(粗实线)横截面示意图

1.2 模型参数设置

本文有限元模拟的初始管坯尺寸为φ81×8mm，成品管尺寸φ45×3mm。轧辊孔型和芯棒的几何参数根据某公司使用的XⅡT-80图纸确定，孔型工艺参数如表1所示，利用三维绘图软件Pro/E分别建立轧辊、工件、芯棒和挡板的实体模型，并在Pro/E中进行装配，然后以stl格式导入DEFROM-3D软件中，建立的三维有限元模型如图2所示。

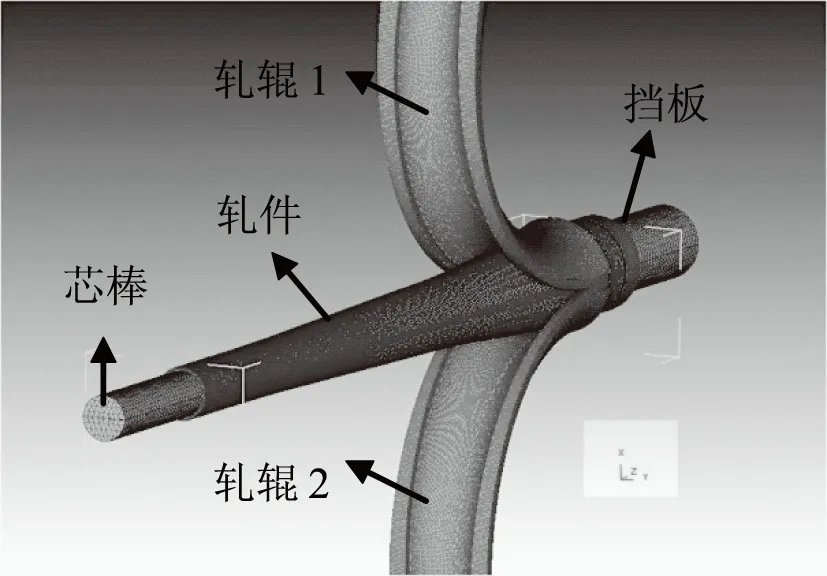
图2 H65黄铜管皮尔格冷轧管三维有限元模型

管坯材质为H65黄铜，其材料参数可直接从DEFORM-3D材料库中导入，管坯定义为塑性体。轧辊、芯棒的材质均采用GCr15钢，其强度和硬度远远高于H65黄铜，在轧制过程仅会发生很小的弹性变形，故本模拟将轧辊、芯棒均定义为刚体。

(1)传热边界条件的设置

为了研究冷轧管过程的温升现象(变形热和摩擦生热)，将模拟控制方式选择为变形和传热的耦合方式，确定传热边界条件时考虑轧辊与坯料的接触热传导、坯料与环境的对流和辐射传热以及润滑乳液与管坯之间的热传导。

计算皮尔格冷轧管过程的温度场时，涉及的内热源有以下两种：一是塑性变形热，即变形热效应，其表达式为

式中：σ为等效应力；ε为平均变形速率；η为塑性功转变热的比例，Wertheimer[7]认为对大多数金属而言，变形功的90%转化成为热量，故这里η取0.9；二是变形区接触摩擦功转化热，单位时间内因轧件与轧辊和芯棒的摩擦而产生的摩擦功均可由(2)式计算：

Wf=μp(φ)νf(2)

式中：μ为摩擦系数；p(φ)为轧制力的法向分量；νf为轧件与轧辊或芯棒的相对速度值；

皮尔格冷轧管过程的轧件的温度场边界面分为自由表面和轧件与轧辊的接触表面，对于自由表面存在对流和辐射以及润滑乳液对管坯的冷却作用，其可统一表示为：

q=H(T-T∞) (3)

H=h+hf+hw(4)

hf=Eσ(T+T∞)×(T2+T∞2) (5)

式中：q为热流密度；H为等效导热系数；T、T∞分别为轧管表面和周围环境温度；h为对流传热系数，这里取0.02KW/(m2.K); hf为辐射传热系数；hw为喷射到管坯的乳液与管坯的传热系数，根据大量的试验数据和模拟结果的吻合程度来看，取值为0.06 KW/(m2.K)较为合理；E为黑度，这里取0.6；σ为玻尔兹曼常数。

对于轧件与轧辊的接触热传导可表示为：

qc=hc(T-Tt) (6)

式中：hc为接触导热系数，本文模拟取hc=11 KW/(m2.K)；T、Tt分别为轧件接触部分表面温度和轧辊接触部分表面温度。

(2)摩擦接触条件的设置

冷轧管实际生产中，由于管坯外表面不断更新润滑乳液对其进行冷却和润滑，而内表面却无润滑，故管坯与轧辊的接触摩擦力相对较小，取剪切摩擦因子f=0.08，而管坯与芯棒和挡板的接触摩擦力相对较大，取剪切摩擦因子f=0.12。

(3)运动条件的设置

模拟皮尔格冷轧管的过程中，为了防止管坯沿轴向发生刚体运动，需要在管坯尾部加一固定挡板。另外，轧制过程中，管坯在X、Y、Z方向都受到力的作用，为了防止轧制出来的管料发生振动和弯曲，需要对成品管前端面增加约束，使Vx=Vy=0(相当于实际导向辊的导向作用)。皮尔格冷轧管过程是轧辊的运动沿管坯轴向的直线运动和绕其自身的轴转动的复合运动，为了实现运动的协调，本文模拟中轧辊的自转速度为10.916rad/s,沿管坯轴向的速度为2406mm/s[8-10]。

2 试验方法

某公司采用“水平连铸管坯—冷轧开坯—拉拔”的技术方案进行了H65黄铜管的生产试验研究，通过开展一系列工艺试验和检测分析，从熔炼、水平连铸、冷轧、拉拔等工艺环节对H65黄铜管高效短流程工艺进行了系统优化。本文重点对冷轧管工艺进行分析研究，本文取得的样品均来自该公司生产试验现场。

将经粗磨、精磨和抛光后的试样进行腐蚀(腐蚀剂为：5g三氯化铁+ 15ml盐酸+100ml蒸馏水)后，在4XC型金相显微镜上观察样品铸态、轧管态的金相组织。

3 结果及分析

3.1 有限元模拟分析结果

(1)温度场分布

正行程开轧时，假设管坯温度分布是均匀的，开轧后管坯的温度场分布取决于塑性变形产生的热效应、接触摩擦生热以及管坯与周围环境的热交换。图3为管坯轧制到第260步时的温度场分布情况，可以看出，孔型侧壁开口处的管坯温度相对较低，其温升主要来自塑性功的转换。而孔型脊部区域的管坯温度相对较高(局部区域高达300℃，红色显示)，其温升是变形热效应和摩擦生热共同作用的结果。另外从

(待续)