基于改进突变级数的区域科技创新能力评价研究

李柏洲，苏 屹

(1.哈尔滨工程大学经济管理学院，黑龙江哈尔滨150001;2.哈尔滨工程大学企业创新研究所，黑龙江哈尔滨15000)

区域科技创新能力是区域创新系统的核心能力，对区域科技创新能力进行科学的评价分析有助于地方政府针对自身特点制定切实合理的科技创新战略，保持和提高区域竞争优势;有助于国家对于全国各区域的创新能力发展有一个科学的认识，通过分析找出宏观政策制定的缺陷，进而找到全国整体经济发展的方法和途径。从已有文献来看，学者主要从模糊数学、SPA联系函数、因子分析法、层次分析法(AHP)、神经网络(RBF)、主成分分析、熵值法、粗糙集法、最优脱层法、密切值法、功效系数法、灰色理论、数据包络分析(DEA)等方面，对区域科技创新能力进行研究［1-10］。由于篇幅的限制，我们省略以上方法的逐项研究的细节，直接给出以上研究存在的缺陷:第一，众所周知，指标体系的构建通常是基于主观经验主义的，当然事实证明这种方法具有一定的科学性和合理性，但是目前的研究模型通常不考虑具体问题的特殊性，没有对指标体系本身构建是否合理的检验;第二，部分研究方法虽然可以达到综合评价的目的，但是评价出来的评价数值只具备相对的含义，缺少绝对的含义，不利于国家进行整体把握我国区域发展情况，且容易给研究者带来评价指标得分的误解。本文将采用结构方程、粗糙集法对突变级数进行改进，对我国不同省市的区域科技创新能力进行实证研究，改进后的突变级数模型可以很好地解决已以上两点问题。

1.突变级数基本理论

突变理论(catastrophe theory)是研究不连续现象的新兴数学分支，它是在系统结构稳定性理论、拓扑学和奇点理论等基础上发展起来的［11］。其主要思想是根据势函数，把临界点分类，进而研究各种临界点附近非连续性态的特征，即有限个数的若干初等突变，并以此为基础探索自然和社会中的突变现象。突变理论建立后，被广泛应用于沉淀过程、地壳中断层运动、线弹性断裂力学和塑性力学中失稳的现象、断裂力学等方面的研究［12-15］。

突变级数模型(系统)的势函数f( x)，其所有临界点集合成一平衡曲面，通过对f( x)求一阶导数，并令f( x)'=0，即可得到该平衡曲面方程。该平衡曲面的奇点集可以通过二阶导数f( x)″=0求得。有f( x)'=0和f( x)″=0可得到由状态变量表示的反应状态变量与各控制变量之间的关系的分解形式的分歧方程。利用突变理论中分歧点集方程与模糊数学相结合推导出突变模糊隶属函数(归一公式)，归一公式将系统内部各控制变量不同的质态归化为可比较的同一种质态。由归一公式进行综合量化运算，最后归一为一个参数，即求出总的隶属函数，从而对评价目标进行排序分析的一种综合评价方法。突变级数法是一种对评价目标进行多层次矛盾分解，该方法的特点是无需计算指标权重，但它考虑了各评价指标的相对重要性，从而减少了主观性又不失科学性、合理性，而且计算简易准确，其应用范围广泛。

2.基于改进突变级数的区域科技创新能力评价研究

我们对传统的突变级数综合评价模型进行改进和完善，具体内容包括:第一，运用结构方程对指标体系的有效性进行检验，以消除由于主观性而带来的评价误差;第二，针对指标个数多于4个的情况，传统方法主要采用因子分析法来进行指标提纯。本文认为这种方法不便于比较指标之间的信息重叠性，容易造成某方面信息的过度加强，因此本文采用粗糙集法对指标进行化简与浓缩，实现个数与信息重叠的双浓缩;第三，传统的突变级数法计算的结果只有相对含义没有绝对含义，这就容易造成对评价结果的误解，基于此本文借鉴数值转换的思想，使得评价的结果也具有绝对的含义。改进后的突变级数评价模型的评价结果更加贴近实际情况，便于相关人员的研究与分析。

(一)改进突变级数法的模型构建

按照以上提到的思路，改进突变级数模型构建如下:

(1)构建指标体系并检验其有效性

按照想要评价问题的情况进行定性分析，构建用于评价的指标体系。任何指标体系的构建都是相对主观的，因此我们采用结构方程法对指标体系的有效性进行检验。结构方程(SEM)是上个世纪70年代，Jöreskog利用数学矩阵的观念将两种范式巧妙整合，开创了一个崭新的量化研究范式，它的一个重要特性就是能够对抽象的概念进行估计与鉴定，其可以看作是不同统计技术与研究方法的综合体。SEM并非单指某种特定的统计方法，而是一套用以分析共变结构技术的整合，以共变结构分析(covariance structure analysis)、共变结构模式(covariancestructure modeling)等不同的名词存在。结构方程以协方差的运用为核心，亦可处理平均数估计，适用于大样本分析，且具有理论先验性［16］。

结构方程分析可粗略分为4大步骤［17］:第一步，模型的构建(model specification)。在该步骤中需要完成的工作主要包括:观测变量(即指标)与潜变量(因子)的关系;各潜变量间的相互关系(指定哪些因子间有相关或直接效应);在复杂模型中，可以限制因子负荷或因子相关系数等参数的数值或关系。

第二步，模型拟合(model fitting)。在建立一个结构方程的模型后，需要设法求出模型的解，其中主要的是模型参数的估计。这个过程称为模型的拟合，如通常所用的最小二乘法你和模型中，相应的参数估计就称为最小二乘法估计。在结构方程分析中，我们的目标是求参数使得模型隐含的协方差矩阵(再生矩阵)与样本协方差矩阵“差距”最小。对于这个矩阵之间的“差距”，有多种不同的定义方法，因而产生不同的模型拟合方法及相应的参数估计。

第三步，模型评价(model assessment)。在评估一个刚刚构建的模型时，需要从以下几个方面入手:第一，结构方程的解是否适当(proper)，其中包括:迭代估计是否收敛(iterated estimate converges)，各参数估计是否在合理范围内(相关系数在-1与+1之间);第二，参数与预设模型的关系是否合理。数据分析可能出现一些预期以外的结果。但各参数绝不应出现一些相互矛盾，与先验假设有严重冲突的现象;第三，检视多个不同类型的整体拟合指数，其中包括:NNFI、CFI、RMSEA 和 χ2等，以衡量模型的拟合程度［18-19］。

第四步，模型修正(model modification)。该步骤主要包括:首先，依据理论或假设，提出一个或数个合理的先验模型;其次，检验潜变量(因子)与指标之间的关系，建立测量模型，有时可能增减或重组题目。若用同一样本数据去修正重组测量模型，再检验新模型的拟合指数，十分接近探索性因素分析(exloratory factor analysis，EFA)所的拟合指数，不足以说明数据支持或验证模型;再次，若模型含多个因子，可以循序渐进的，每次只检验含两个因子的模型，确立测量模型部分的合理后，最后再将所有因子合并成预设计的先验模型，做一个总体检查;第四，对每一个模型，检验标准误、t值、标准化残差、修正指数、参数期望改变值、χ2及各种拟合指数，据此修改模型并重复第三和第四步;最后，这最后的模型是依据某一样本数据修改而成，最好用另一个独立样本交互确定。

传统突变级数法的指标体系通常是主观定义得出的，这种以经验为主的方式会给指标体系带来一定的主观性，进而影响综合评价结论的可信度，通过以上的方法可以对指标体系的有效性进行科学的检验，进而实现突变级数法的第一步改进。

(2)指标个数检验

计算经过结构方程验证的指标体系的各层次的指标个数，对于多于4个指标的层次应用粗糙集法进行个数和信息的浓缩。粗糙集(rough set，RS)理论可以从大量的数据中挖掘潜在的、有利用价值的知识，常用于处理模糊和不精确的问题。粗糙集把知识理解为对对象的分类能力，它包含了知识的一种形式模型，这种模型将知识定义为不可区分关系的一个族集［20］。粗糙集使得知识有一个清晰定义的数学意义，而且可使用数学方法来分析处理。成员的关系不再是一个初始概念，而是客观计算的，只与已知知识有关。应用粗糙集法的步骤主要有［6］:

首先，确定决策规则表。知识表达系统的表示形式为s=(U，R，V，f)，其中:U是对象的集合，即论域;R=C∪D是属性集合，C∪D=(子集C和D分别为条件属性和决策属性);V为属性值的集合;f:U∪R→V是一个信息函数，表示U中每一个对象x的属性值。具有条件属性和决策属性的知识表达体系就构成了决策表。本研究中研究样本用来代表，即 X1，X2，…Xn代表不同省、地区代表科技创新能力评价的指标体系，即F1，F2…，Fm代表依据选取原则所选中的评价指标。

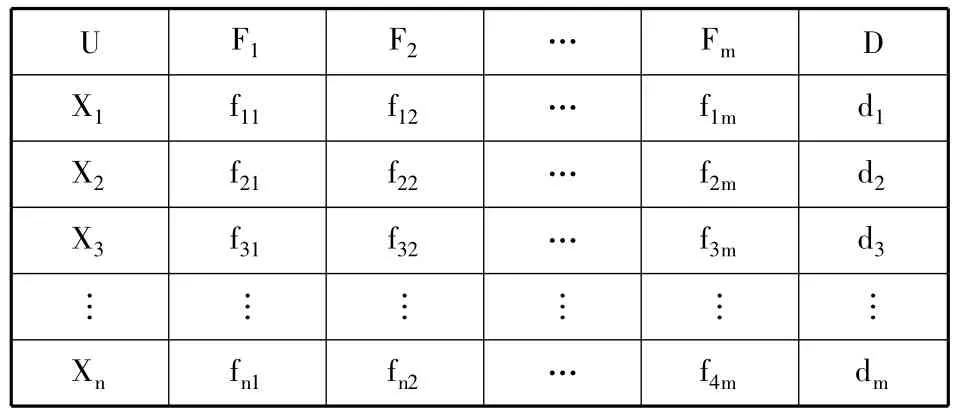
表1 决策规则表

其次，进行数据离散化。以指标的平均水平为参考点进行数据离散化处理，当指标优于全国平均水平时取1，否则取0，处理后所得到的数据为离散型数据。最后，进行属性简约。令S=(U，A，V，f)是一个知识表达系统，S的区分矩阵是一个n×n矩阵，其中任一个元素可表示为:

区分函数表示为:

其中区分函数Δ有如下性质:函数Δ的极小析取范式中的所有合取式是属性集A的所有约简，经过以上计算解决了传统因子分析法仅对指标个数进行缩减，而没有考虑指标信息方面的浓缩，实现了突变级数的第二步改进。

(3)识别突变系统类型

突变系统类型一共有7个——折叠突变、尖点突变、燕尾突变、蝴蝶突变、双曲脐突变、椭圆脐点突变、抛物脐点突变，其中常见的形式有:尖点突变、燕尾突变和蝴蝶突变。

其中f( x)表示一个系统的一个状态变量x的势函数，状态变量x的系数a、b、c、d表示该状态变量的控制变量。指标可分解为2、3、4个子指标，则该系统可分别视为尖点突变系统、燕尾突变系统、蝴蝶突变系统。

(4)数值转化

设底层指标对应的隶属度值均取为x，则从理论意义上讲，此时评价总体的综合评价值也应为x。设当底层指标对应的隶属度值均取为 xi(i=1，2，…，n)时，由突变评价法(具体计算方法参照(3)、(5))进行计算，可得到其综合评价值为yi(i=1，2，…，n)。当n足够多时，则可建立起yi与xi之间的对应关系表。由yi与xi之间的对应关系表，可将yi值变换为对应的xi值。由于底层指标的隶属度取值具有习惯意义上的“优”、“劣”概念，因此变换后的突变评价值也具有习惯意义上的“优”、“劣”概念［21］，进过此种变换解决了传统突变级数法没有绝对含义的限制，实现了突变级数的第三步改进。

(5)归一公式的计算及综合评价

根据突变系统的分叉方程导出3种常见形式的归一公式:尖点突变归一公式为尾突变归一公式为;蝴蝶突变归一公式为

根据多目标模糊决策理论，同一方案在多种目标情况下，设A1，A2，…Am为模糊目标，则理想的策略为:C=A1IA2I，…Am，其隶属函数为:μ(x)=μA1(x)∧μA2(x)∧…∧μAm(x)，式中 μAi(x) μAi(x)为Ai的隶属函数，定义为此方案的隶属函数，即为各目标隶属函数的最小值。

对于不同的方案，如设 G1，G2，…Gn，记 Gi的隶属函数为u( Gi)，则表示方案 Gi优于方案Gj。因而利用归一公式对同一对象各个控制变量(即指标)计算出的对应的X值应采用“大中取小”原则，但对存在互补性的指标，通常用其平均数代替，在对象的最后比较时要用“小中取大”原则，即对评价对象按总评价指标的得分大小排序［22］。

(二)实证研究

(1)指标体系的构建

在考虑区域科技创新能力的结构方程模型中潜在变量和观测变量时，要体现区域科技创新的能力、效果、效率，同时也要在区域技术实力所依靠的基础、区域科技创新的可持续性和发展潜力等方面有所体现［23］。因此，一方面须包含资源投入、经济效益产出指标，又需考虑区域经济发展水平、高新技术及可持续性指标，以保证指标的科学合理性和可验证性;另一方面要充分考虑各区域间差异，基于此确定观测变量16个，潜在变量2个，具体内容如表2中所示。

表2 潜在变量与观测变量的确定

潜在变量 观测变量全员劳动生产率(B1)高科技产品占出口总额(B2))高科技产业规模以上企业产量(B3创新系统网络环境人均GDP(B4)外资直接投资(B5)区域出口额(B6)

(2)指标体系的有效性检验

我们采用结构方程法首先来对指标体系的有效性进行检验，应用LisWin32软件，通过编程实现科技创新能力的结构方程运行。本实证的数据来源于2008年的国家统计年鉴，表3为无纲量化处理后的数据。

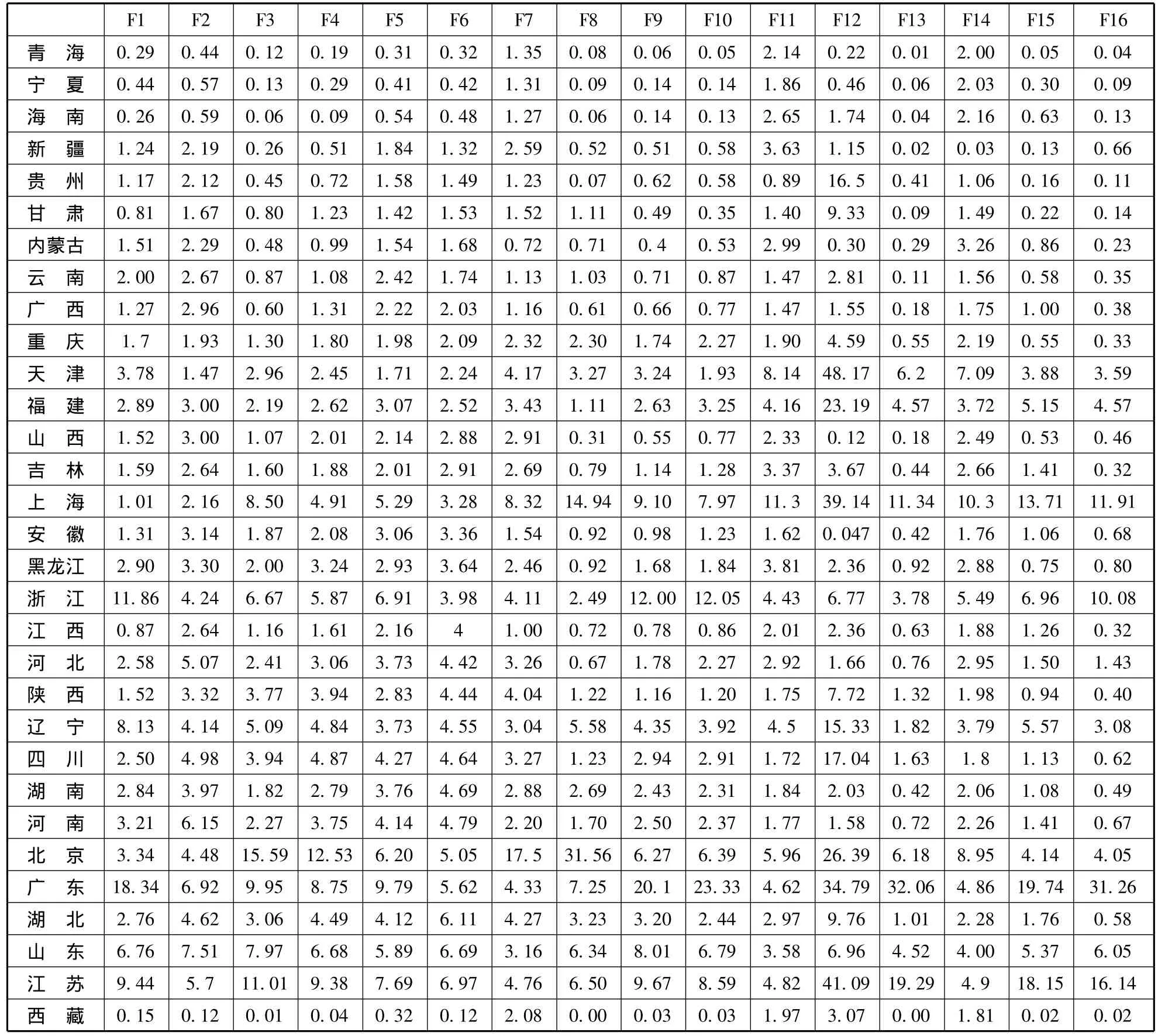
表3 无纲量化处理后的指标评价体系

通过对数据的计算得出观测变量的相关矩阵为对称矩阵，因此我们只给出下三角矩阵:

第一，T值检验。

软件计算的输出结果:

LAMBDA-X

区域创新系统各主体要素 创新系统网络环境

模型输出结果:

每个参数(自由估计的元素)对应于三个数值，第一个是参数估计，第二个是标准误差(standard error)，第三个是t值。从输出结构我们可以发现16项的t值均大于2，我们认为结论是显著的。

第二，拟合优度统计量检验。

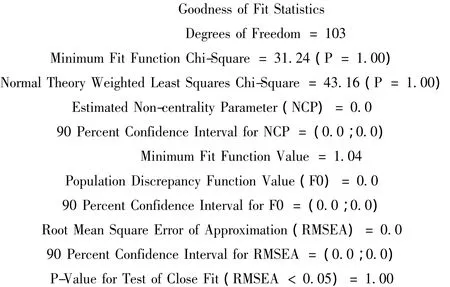
在此处我们主要检验平均概似平方误根系数(RMSEA)、NFI、NNFI、CFI等指标，其中 RMSEA 越小越好，在0.08以下可以接受;NFI、NNFI、CFI则是越大越好，通常认为其值在0.9以上为好。从模型的输出结果来看，该模型的RMSEA=0＜0.08，但是 NFI=0.8 ＜0.9，根据相关文献可知［16］，NFI的测量值受到样本个数和自由度的限制较大。由于受到统计年鉴的限制，本例中的样本数量相对不是很多，在此种样本数量不是很大的情况下，可以采用NNFI代为检测。本例中，NNFI=3.12＞0.9，这说明模型的拟合程度很好，同时模型的CFI=1＞0.9，模型无需修正，即本文构建的区域科技创新能力的指标体系是科学、合理的。

(3)指标个数与信息浓缩

通过上文的介绍可知，应用突变级数模型时，指标的个数一定要控制在4个以内，在检验了指标体系有效性的基础之上，若基层指标的个数多于4个，需要对指标进行变换，数据同样取自表3。结合上文所提的粗糙集理论，构建区域创新能力评价指标的知识系统。按照表2中观测变量的顺序将条件属性分别定义为F1，F2…，F16。以各省和地区指标的平均水平为参考点进行数据离散化处理，当指标优于全国平均水平时取1，否则取0，处理后所得到的数据为离散型数据，数据如表4所示。

通过对离散数据的合并、计算得出区分矩阵法，得到知识系统的核为:{F1F4F6F8F11F12F13F14}，即科技经费投入量、R＆D人员数、高等教育专任教师、技术市场人均成交额、全员劳动生产率、高科技产品占出口总额、高科技产业规模以上企业产量和人均GDP等8个指标是评价区域科技创新能力的核心指标，如表5所示。

表4 离散化的区域科技创新能力指标评价体系

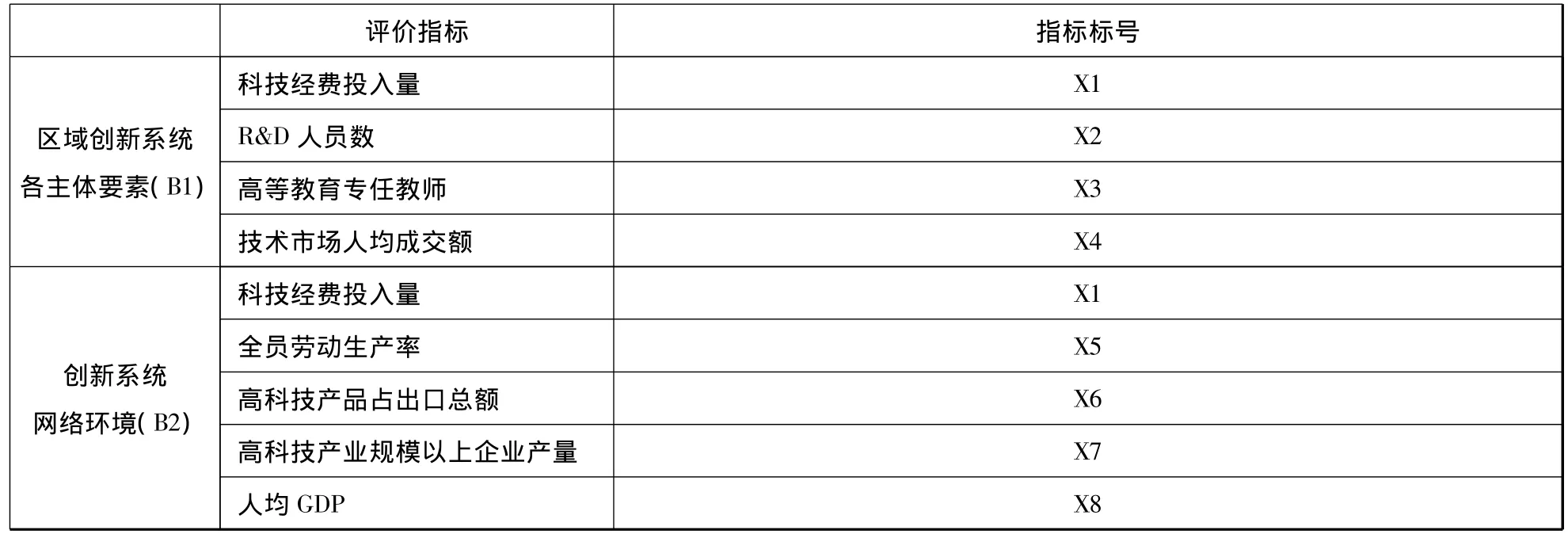
表5 优化后的科技创新能力评价指标体系

(4)指标数值的转化

按照上文构建的模型，分别设当底层指标对应的隶属度值均取为xi(i=1，2，…，11)时(xi的值来自于表3)，由突变评价法进行计算，可得到其综合评价值为yi(i=1，2，…，11)，具体计算数值见表6，此时用 yi的值代替 xi。

表6 指标数值转换

(5)归一公式计算

通过上文的分析和计算可以知道，该评价问题每层涉及到4个可量化指标，因此可以选择蝴蝶突变。由于四个指标之间都是相互补充的关系，因此在计算过程中应该选择互补型蝴蝶突变。在这里我们不再重复上文构建模型的计算过程，按照模型计算出来的结果如表7所示:

表7 归一化公式计算结果

续表 归一化公式计算结果

续表 归一化公式计算结果

续表 归一化公式计算结果

(6)利用归一公式进行综合评价。

B1、B2之间是非互补尖点型突变级数模型，按照上文构建的模型进行计算，评价得分选取原则按照取小原则，具体数值见表8:

表8 评价得分计算结果

表9 最终评价结果

按照表8给出的数据，对全国省市进行综合排序，同时改进后的突变级数模型的评价结果具有绝对含义，因此给出相应省市的评价等级，具体见表9。

(三)实证结果分析

表9给出了我国30个省市的区域科技创新能力强弱的排序，并且基于改进的突变级数法计算出的结果具有绝对含义，通过结果我们可以得出:发展处于优秀状态的区域有广东、江苏、北京3个省市;发展处于良好状态的区域有浙江、辽宁、山东、湖北、上海5个省市;发展处于中等状态的区域较多有四川、天津、河南、陕西、黑龙江等14个省市;发展处于一般状态的区域有广西、内蒙古、甘肃、新疆5个省市;处于较差状态的区域有:宁夏、青海、海南3个省市。从全国的实际情况来看，对比已有文献的研究成果，本文的研究结论基本上符合现实，这说明了改进突变级数的有效性。

在计算的过程中，本文也完成了全国30各省市聚类的分析，这对于国家制定相关的区域发展战略、借鉴相关区域的对比研究具有重要的意义。我们将具有绝对含义的评价结果采用图标的形式表示出来，具体如图1所示。其中，横坐标表示评价的等级，0-1之间表示区域科技创新能力极差(评价得分在0-50之间)，1-2表示区域科技创新能力较差(评价得分在50-60之间)，以此类推，4-5表示区域科技创新能力优秀(评价得分在90-100之间);纵坐标表示省市个数，图2中的曲线勾画出了我国各省市处于不同阶段的情况。从图形中我们可以辨认出，我国目前各省市的分布情况符合正态分布。虽然从个别省市的角度来说，他们的发展可能存在问题，区域科技创新能力有待加强，但是从国家整体来看，这一时期的宏观政策调控是合理和有效的。

图1 各省市能力分布情况

3.结论

本文在总结回顾区域科技创新能力评价模型的基础上，指出已有评价模型存在的缺陷，并运用突变级数法进行研究。但是传统的突变级数法也存在一些弊端，因此本文结合结构方程、粗糙集理论和数值转换方法构建了一个更加科学、合理的综合评价模型——改进突变级数综合评价模型，该模型具有很好的可移植性。改进后的突变级数评价模型可以对指标体系的合理性进行验证，对不符合突变级数要求的指标进行信息和数量的双浓缩，同时综合评价结果具有绝对含义。最后，选取全国省市为样本进行实证研究，一方面，对各省市区域科技创新能力进行了排名;另一方面，由于改进后的突变级数具有绝对数值的含义，因此我们可以采用这一评价结果对国家宏观政策的运行效果进行分析。

［1］唐炎钊.区域科技创新能力的模糊综合评价模型及应用研究——2001年广东省科技创新能力的综合分析［J］.系统工程理论与实践，2004，(2):37-43.

［2］荣飞，刘春凤.区域科技创新能力评价与态势分析［J］. 河北大学学报，2006，(6):48-51.

［3］杨大楷，冯一体.长江三角洲区域科技创新能力实证研究［J］.上海财经大学学报，2008，(6):80-90.

［4］冯岑明，方德英.基于RBF神经网络的区域科技创新能力的综合评价研究［J］.科技进步与对策，2007，(10):140-143.

［5］杨艳萍.区域科技创新能力的主成分分析与评价［J］.技术经济，2007，(6):15-20.

［6］李柏洲，苏屹.区域科技创新能力评价体系的优化及实证分析［J］.情报杂志，2009，(8):80-83.

［7］Chung-Jen Chen，Chin-Chen Huang.A Multiple Criteria Evaluation of High-tech Industries for the Science-based Indus-trial Park in Taiwan［J］.Information ＆ Management，2004，41:839-851.

［8］刘国新，冯德雄，姚汉军等.区域创新创业能力的综合评价［J］.武汉理工大学学报:信息与管理工程版，2003，(1):84-88.

［9］罗亚非，李敦响.基于密切值法的不同类型企业技术创新能力评价研究［J］.评价与预测，2005，(11):83-84.

［10］冯邦彦，李胜会.我国自主创新实现能力及转化能力评价［J］.科学学与科学技术管理，2006，(12):67-70.

［11］桑博得.突变理论入门［M］.凌复华译.上海:上海科学技术文献出版社，1988.

［12］Cubit J，Shaw B.The Geological Implication of Steadystate Mechanisms in Catastrophe Theory［J］.Math Geology，1976，8:657-661.

［13］Henley S.Catastrophe Theory Models in Geology ［J］.Math Geology，1979，8:6-11.

［14］Potier-Ferry M.Towards a Catastrophe Theory for the Mechanics of Plasticity and Fracture［J］.International Journal of Engineering Science，1985，23(8):821-837

［15］Alberto Carpinteri.A Catastrophe Theory Approach to Fracture Mechanics［J］.International Journal of Fracture，1990，44(1):57-69.

［16］邱皓政，林碧芳.结构方程模型的原理与应用［M］.北京:中国轻工业出版社，2009.

［17］侯杰泰，温忠麟，成子娟.结构方程模型及其应用［M］.北京:教育科学出版社，2004.

［18］MacCallum R C，Browne M W，Sugawara H W.Power Analysisand Determination of Sample size for Covariance Structure Modeling［J］.PsychologicalMethods，1996，(1):130-149.

［19］Marsh H W，Balla J R.Goodness-of-fit Indices in Confirmatory Factor Analysis:The Effect of Sample Size and Model Complexity［J］.Quality ＆ Quantity，1994，(28):185-217.

［20］王彪，段禅伦，吴昊等.粗糙集与模糊集的应用及研究［M］.北京:电子工业出版社，2008.

［21］施玉群，刘亚莲，何金平.关于突变评价法几个问题的进一步研究［J］.武汉大学学报，2003，(4):132-136.

［22］陈晓红，彭佳，吴小瑾.基于突变级数法的中小企业成长性评价模型研究［J］.财经研究，2004，(11):5-16.

［23］李晓路，周志方.我国区域技术创新能力体系评价及提升——基于因子分析法的模型构建与实证检验［J］.科学管理研究，2006，(2):5-10.