地暖系统的量子遗传约束广义预测控制
2012-07-26吴忠强郄程飞
吴忠强 郄程飞
(燕山大学电气工程学院工业计算机控制工程河北省重点实验室,河北 秦皇岛 066004)
0 引言
地板辐射采暖系统(简称地暖系统)作为一种新兴的采暖末端装置,以其节能、舒适、卫生等优点而逐渐被消费者所接受[1-3]。在理想情况下,可将地暖系统看作一个参数不确定的线性无约束大惯性系统。在室内空气温度达到预设值的实际过程中,要求地暖系统控制器的输入、输出信号满足多种约束条件[4-5]。
广义预测控制在广义最小方差控制的基础上,在优化过程中引入多步预测的思想,具有较强的鲁棒性。对于过程参数慢时变系统,广义预测控制易于在线估计参数,实现自适应控制。因此,本文提出一种将约束条件引入广义预测控制的方法,并将其应用于地暖控制系统中。但将约束广义预测控制应用于参数不确定的地暖系统后,会使求解控制量的滚动优化问题变得复杂,导致迭代求解的计算量较大。对此,本文引入量子遗传算法滚动优化广义预测控制的控制增量Δu(k)。试验表明,该算法取得了较好的控制效果。
1 地暖系统数学模型建立
地暖系统模拟结构如图1所示[6-7]。

图1 地暖系统模拟结构图Fig.1 Simulative structure of floor heating system
图1中:标号1~4分别为系统的四个热平衡点;tha为房间空气温度;ts为地板温度;th为水泥砂浆填层的上表面温度;tst为供暖管表面温度;tfp为供暖管中的热水温度,作为控制量;tbo为保温层的温度;tw为室外空气温度,设tw=0℃;trp为室内平均辐射温度;k0为室内外空气传热系数;k'0为吊顶与室内空气的传热系数,可近似认为k'0=α0;α0为房间内空气的传热系数;k1为地面面层材料的传热系数,本文选择瓷砖作为面层材料;k2为水泥砂浆填层的传热系数;k3为保温层泡沫传热系数;k4为供暖管管壁的传热系数。
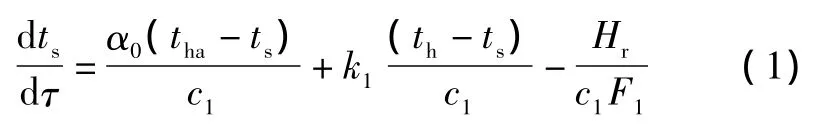
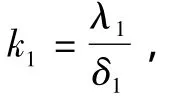
由平衡点2的热平衡关系,得到热平衡方程如式(2)所示:
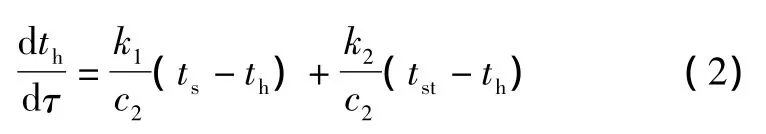
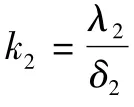
由平衡点3的热平衡关系,得到热平衡方程如式(3)所示:

式中:供暖塑料管热容 c3=cρ3ρ3δ3。
由于泡沫保温层的热阻隔作用,可假设地暖系统不存在向下的热传导。
由平衡点4的热平衡关系,得到热平衡方程如式(4)所示:

式中:房间空气热容 c0=cρ0ρ0v0,其中,cρ0、ρ0和 v0分别为房间空气的比热、密度和房间体积;Fi为各墙壁的面积。
取状态变量x=[tsthtsttha]T,系统输入 u=tfp,系统输出 y=tha,得到该地暖系统的状态方程如式(5)所示:
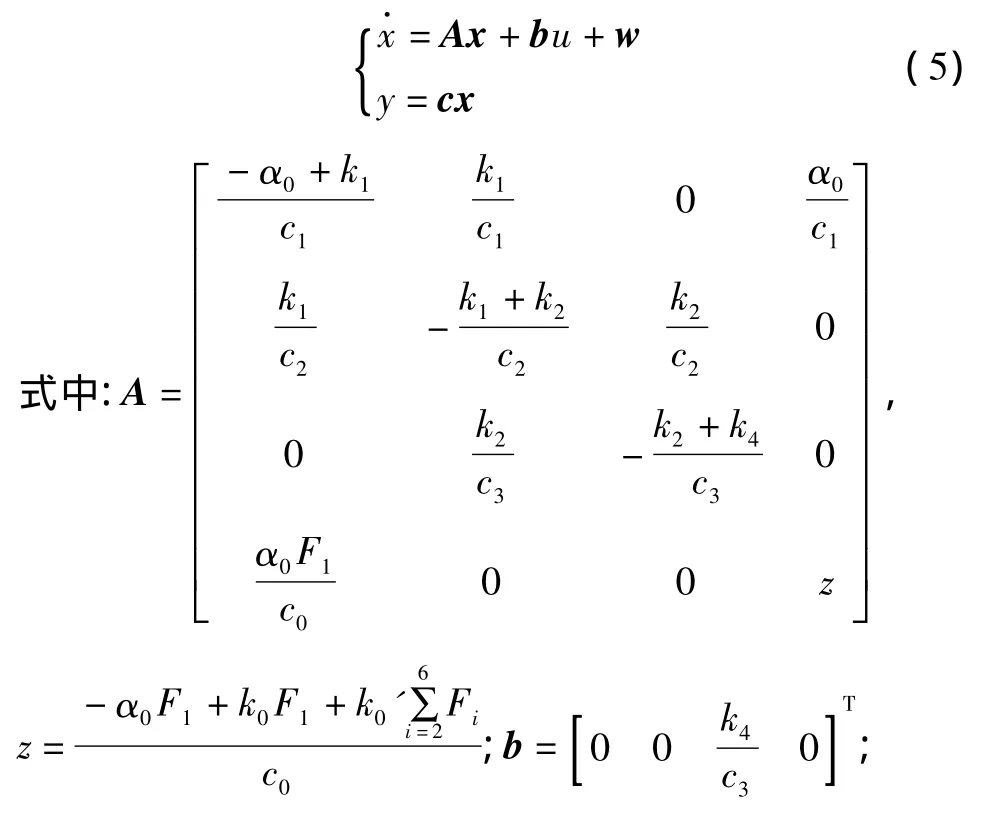

以某房间为实际研究对象,房间的长、宽、高分别为7.8 m、6.3 m、3.5 m;房间空气的参数为cρ0=1.007 kJ/(kg·℃)、ρ0=1.169 1 kg/m3、v0=172 m3、α0=22.5 W/(m2·K)、k0=4.005 W/(m2·K)[8];瓷砖参数为cρ1=2 300 kJ/(kg·℃)、ρ1=2 083 kg/m3、δ1=0.01 m、λ1=1.1 W/(m·K);水泥砂浆的参数为 cρ2=920 kJ/(kg·℃)、ρ2=2 300 kg/m3、δ2=0.03 m、λ2=1.51 W/(m·K);供暖塑料管的参数为 cρ3=950 kJ/(kg·℃)、ρ3=940 kg/m3、δ3=0.002 m、λ3=0.41 W/(m·K)。
将参数代入地暖数学模型中,得到如式(5)所示的状态方程为:b=[0 0 0.114 781 63 0]T、c=[0 0 0 1]。
以T=200 s为采样周期,将数学模型离散化,再转化为传递函数形式,整理为受控自回归积分滑动平均模型的形式,如下式所示:
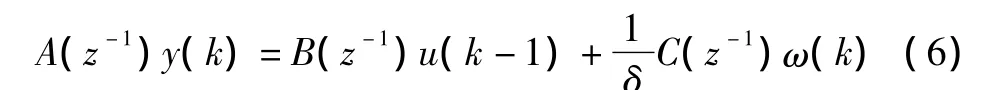
式中:A(z-1)=1-0.515 1z-1-1.205z-2+0.368 4z-3+0.248 9z-4;B(z-1)=0.002 763+0.011 05z-1+0.016 58z-2+0.011 05z-3+0.002 763z-4;C(z-1)=1;δ=1- z-1,为差分因子;ω(k)为不确定扰动,包括由冷空气进入房间所引起的外界干扰量Hr和墙体与室内空气之间的换热。
2 约束广义预测控制
广义预测控制是以受控自回归积分滑动平均模型(controlled auto regressive integrated moving average,CARIMA)为基础,采用了长时段的优化性能指标,并结合辨识和自校正机制的预测算法[9-10]。
设预测步长为P,控制步长为L。系统从第k个采样时刻起,未来L个控制增量Δu(k+1),…,Δu(k+i),…,Δu(k+L)通过量子遗传算法(quantum genetic algorithm,QGA)得到。这些增量随着时间的推移不断向前滚动,最终得到未来L个控制量u(k+1),…,u(k+i),…,u(k+L)。其中:
由CARIMA地暖数学模型,计算得到系统预测输出y(k+1)并反馈到优化指标。优化指标中引入了对输出误差和控制增量加权的二次型性能指标,并加入了对系统控制量和控制增量的约束,即对地暖系统的输入量u(k)和输入变化量Δu(k)的约束。用不等式的形式描述上述性能指标,得到在k时刻的优化性能指标及约束条件如式(8)~式(10)所示。
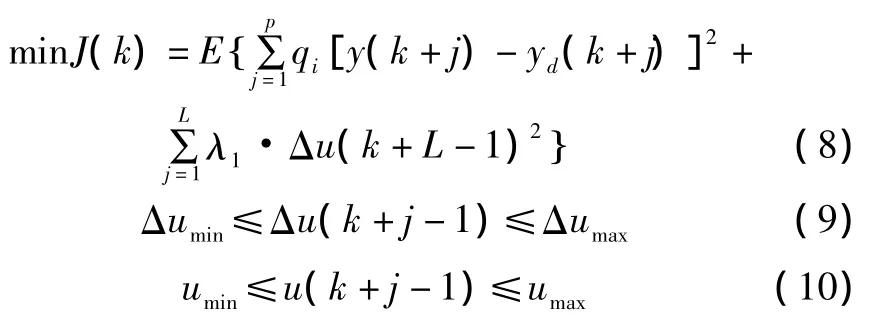
式中:qi为输出误差系数;λi为控制量加权系数,一般取常数值;yd(k+j)为输出值y(k)至设定值S的输入参考轨迹。yd(k+j)的表达式为:

式中:β为柔化系数;S为预设室内空气温度值。
3 量子遗传算法
量子遗传算法(QGA)是基于量子比特和量子叠加态的概念提出的[11-13]。该算法采用了量子比特编码,|0>和|>1表示微观粒子的两种基本状态,称为量子比特。一个量子位的状态可以描述如下:

式中:|φ>表示量子位的当前状态;α、β为复数,分别对应量子态被观测为|0>态和|1>态的概率,且α、β满足归一化条件|α|2+|β|2=1。如果一个系统具有m个量子位,则该系统可同时描述2m个状态。与传统的二进制位编码相比,量子遗传算法的优点在于一个量子位不仅可以处于|0>态和|1>态,而且还可以处于这两个量子位中间的任意一个叠加态。
由于量子系统能够描述叠加态,因此,基于量子比特编码的量子染色体,比传统进化算法具有更好的种群多样性,且当|α|2或|β|2趋近于0或1时,多样性消失,量子染色体会收敛到一个确定的状态,从而获得较好的收敛性。这表明了量子染色体同时具有探索和开发的能力。本文采用量子比特来编码多状态基因作为广义预测控制中的控制增量Δu(k),编码形式如下所示:

3.1 适应度函数的选择
量子遗传算法适应度函数可以由广义预测控制优化性能指标式(8)变换得到,其形式如式(14)所示:

通过该形式的变换,GPC优化指标J的极小值问题即转化为量子遗传算法优化的极大值问题,且在该优化算法运行中,适应度函数值始终位于[0,1]区间。
3.2 算法的实现
与遗传算法类似,量子遗传算法也是一种概率搜索算法,算法优化步骤具体如下[14]。
③算法进入循环迭代阶段,随着迭代的进行,种群的解向最优解不断收敛。在每一次迭代中,先对种群Q(t-1)进行测量,获得一组确定解P(t);随后计算符合约束条件的解P(t)的适应度值;再根据当前的演化目标和调整策略,利用量子旋转门R(t)更新种群Q(t)。选择P(t)中的当前最优解,若该当前最优解优于之前存储的最优解,则用该当前最优解将其替换。
此外,在利用量子旋转门更新种群的过程中都必须保证新个体满足约束条件,防止在种群迭代计算中出现不满足约束条件的个体,从而保证结果的有效性。同时,由于量子染色体本身具有由量子叠加态而导致的个体多样性,没有必要再使用交叉、变异等遗传算子。在QGA中,种群规模即量子染色体的数量始终是恒定不变的,并且使用了量子叠加态,所以QGA比普通遗传算法具有更好的种群多样性和收敛性,并能够得到全局最优解。
3.3 量子旋转门的选择
量子染色体qj的更新是通过量子旋转门R(t)来实现的,其中第 ik个量子位(αik,βik)的更新过程如式(15)所示:

式中:旋转角 θik=S(αikβik)·Δθik,其旋转方向 S(αikβik)和旋转大小Δθik根据事先设定的调整策略来确定[15-16],具体策略如表1所示。
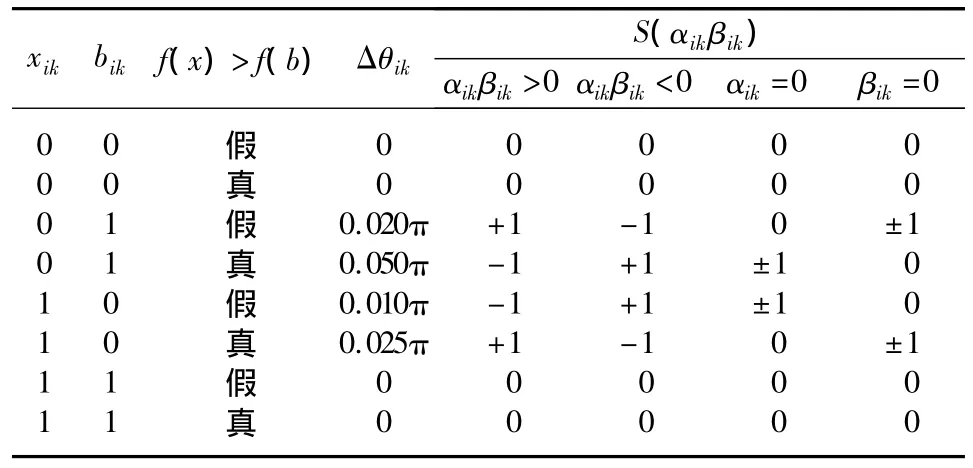
表1 量子旋转门调整策略Tab.1 Adjustment strategy of quantum rotating gate
表1中:f(x)为目标函数;bik和xik分别为最优解和当前解中的第ik个值。当f(x)>f(b)、xik=1、bik=0时,可将 Δθik设置为 0.025π。S(αikβik)决定了收敛到全局最优解的方向,可依据αikβik的具体情况分别设置为+1、-1或0,以增大量子态|1>的概率幅值。Δθik的值直接影响收敛速度。如果Δθik取值过大,容易引起早熟收敛,一般它的取值范围在0.005π~0.05π之间。
4 仿真与试验
基于量子遗传算法的约束广义预测控制器参数取P=3、L=2、λ =0.9、β =0.8、q=1。量子遗传算法设定参数为初始种群Q(t)个数50、遗传代数100、控制增量约束Δu∈[-5,5]、室内温度预设值25℃。为了说明本算法的有效性,与常规广义预测控制方案进行比较,由梯度法寻优得到常规广义预测控制的最优控制律如式(16)所示[8]:

式中:ΔU(k+1)=[Δu(k+1) Δu(k+2)]T;Yd(k+1)=[yd(k+1)yd(k+2)yd(k+3)]T;误差系数阵Q=diag[1 1 1];控制系数阵 R=diag[0.9 0.9 0.9];ΔV(k-1)=[Δu(k-3) Δu(k-2) Δu(k-1)]T;Y(k)=[y(k-3)y(k-2)y(k-1)y(k)]T。
QGAGPC与GPC控制作用下的输出仿真结果如图2所示。
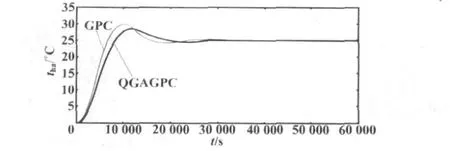
图2 输出仿真曲线Fig.2 Output simulation curves
由图2可以看出,常规广义预测控制反应时间较短,具有快速性,但是超调较大,而且在控制过程中振荡过程时间较长,恒温环境的舒适度较差;在控制初始过程中需要较高的输入值u,即需要较高的供暖热水温度,能源消耗较大。而采用基于量子遗传算法的约束广义预测控制方法的系统输出反应时间稍长,但室内空气温度变化超调小且振荡少,能够较快地达到预设温度值,符合人体对空气温度的舒适度的要求;控制输入u的变化也较为平稳,即对供暖水的温度要求较低,从而实现了节约能源目的。此外,控制输入u的振荡也会相应减少,避免了设备的频繁动作,从而延长了设备的使用寿命。
在实际生活中,许多不确定的因素导致房间空气温度的急剧变化。例如门窗突然打开一段时间,再关上门窗,导致室内空气温度骤降。因此,为了验证控制器的鲁棒性,假设在室内空气温度稳定后,在T=4×104s时对系统施加一个脉冲扰动,脉冲作用时间为Tr=400 s。QGAGPC与GPC控制的鲁棒性比较仿真结果如图3所示。

图3 鲁棒性仿真曲线Fig.3 Robustness simulation curves
从图3可以看出,实际输出值在受到冷空气干扰后,以对流方式与室内空气进行热交换,导致室内空气温度下降,而在系统控制作用下,室内空气温度又逐渐恢复到期望的温度值。在温度恢复过程中,与常规广义预测控制相比较,基于量子遗传算法的约束广义预测控制的系统输出较为平缓,动态降落量小,不会使人感觉到剧烈的温差变化。
考虑到地暖模型参数的不确定性,本文对产生参数摄动的被控对象也进行了仿真研究。
此时,在本文控制方法下的系统输出如图4所示。

图4 系统输出曲线Fig.4 Output curves of system
由图4可以看出,当模型参数产生摄动时,系统在本文所采用的控制方法的作用下同样能够较快地达到稳定输出。当一个不确定扰动作用于稳定输出的系统时,系统同样表现出了较强的鲁棒性。
5 结束语
量子遗传算法是一种新兴的优化算法,与其他优化算法相比较,它具有高度的种群多样性、收敛速度快等优势。本文将量子遗传算法应用于地暖控制系统的约束广义预测控制中,仿真结果表明,基于量子遗传算法的约束广义预测控制的控制效果优于常规广义预测控制。优越性主要表现在超调量明显减少和振荡较少,能够使实际输出值较快的达到预设温度值,并满足人体对温度舒适度的要求。此外,控制系统具有较强的鲁棒性,在实际应用中具有重要意义。
[1]王立璞,李金平,王磊磊,等.太阳能低温地板辐射采暖系统简介及经济性分析[J].中国建设动态:阳光能源,2006(6):39-42.
[2]王子介.地板供暖及其发展动向[J].暖通空调,1999,29(6):35-38.
[3]谢慧.热管地板辐射供暖基础理论研究[D].天津:天津大学,2006.
[4]Bi Qiang,Cai Wenjian,Wang Qingguo,et al.Advanced controller autotuning and its application in HVAC systems[J].Control Engeering Practice,2000,8(6):633-644.
[5]Cao G Q,An D W,Lou C Z.Application of fuzzy self tuning PID control to air conditioning systems[J].Journal of Heating,Ventialtioning and Air Conditioning,2004,34(10):106-109.
[6]王子介,夏学鹰.地板辐射供冷/暖的简化动态模型及其应用[J].南京师范大学学报:工程技术版,2004,4(1):1-3.
[7]杨德伟,王振兴.地板采暖传热过程分析[J].工程热物理学报,2007(3):472-474.
[8]Incropera F P,DeWitt D P,Bergman T L,et al.Fundamentals of heat and mass transfer[M].University of Notre Dame,Indiana,USA,2006.
[9]舒迪前.预测控制系统及其应用[M].北京:机械工业出版社,2001.
[10]诸静.智能预测控制及其应用[M].杭州:浙江大学出版社,2002.
[11]李士勇,李盼池.量子计算与量子优化算法[M].哈尔滨:哈尔滨工业大学出版社,2009.
[12]王凌.量子进化算法研究进展[J].控制与决策,2008,23(12):1322-1323.
[13]Zhang G X,Li N,Jin W D,et al.A novel quantum genetic algorithm and its application[J].Acta Electronica Sinica,2004,32(3):476-479.
[14]Yang S Y,Liu F,Jiao L C.The quantum evolutionary strategies[J].Acta Electronica Sinica,2001,39(12A):1873-1877.
[15]杨淑媛,焦李成,刘芳.量子进化算法[J].工程数学学报,2006,23(2):236-240.
[16]Gu J W,Gu X S,Gu M Z.A novel parallel quantum genetic algorithm for stochastic job shop scheduling[J].Journal of Mathematical Analysis and Applications,2009,355(1):63-81.
