不要被表面现象迷惑

2012-07-25江苏封国云

读写算(下) 2012年5期

关键词：减数正比例份数

江苏封国云

同学们在判断两种量是否成比例、成何种比例时，往往会受题中表面现象的迷惑，出现以下三种错误现象。

一、看到题中有“一定”二字，就误认为要判断的两种量必成比例

病例1判断：（1）下面是小明不同年龄时的体重情况记录表（见下表）。由于小明的体重与对应年龄的比的比值是一定的，所以小明的体重和年龄成正比例。（）

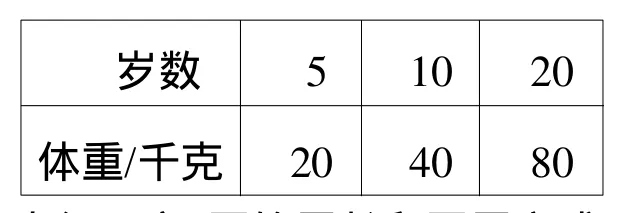
岁数 5 10 20体重/千克 20 40 80

（2）圆的直径一定，圆的周长和圆周率成正比例。（）

（3）被减数一定，减数和差成反比例。（）

病症（1）√ （2）√ （3）√

诊断（1）表中“体重”与“年龄”所对应的比值虽然一定，但这是两种不相关的量，所以体重与年龄不成比例；（2）“圆周长”与“圆周率”虽是两种相关的量，但它们不同时发生变化，其中圆周率是固定不变的，所以圆的周长和圆周率不成比例；（3）“减数”与“差”虽是两种相关的量，且同时变化，但当被减数一定时，它们之间仅仅是和一定，所以减数与差不成比例。

处方（1）×（2）× （3）×

二、看不到题中有“一定”二字，就误认为要判断的两种量必不成比例

病例2判断：（1）订阅《读写算》的钱数和份数不成比例。（）

（2）非零自然数和它的倒数大小不成比例。（）

病症（1）√（2）√

诊断题（1）中的一定量是隐藏着的，即“《读写算》的单价”，也就是订阅《读写算》的钱数和对应份数的比的比值一定，所以订阅《读写算》的钱数与份数不但成比例，而且成正比例；题（2）中也有一个隐含的一定量，即任何一个非零自然数和它的倒数的乘积必定等于1，所以非零自然数和它的倒数大小不但成比例，而且成反比例。

处方（1）×（2）×

三、看到题中有比号或乘号就误认为要判断的两种量必成正比例或反比例

病例3判断：（1）由6︰x=y，可知x和y成正比例。（）

（2）由8×m=n，可知n和m成反比例。（）

病症（1）√ （2）√

诊断像（1）、（2）这样的式子，在判断时通常要先变形，转化成形如x︰y=k(k一定)或xy=k(k一定)的形式，这里的“k”代表常数，也就是式子中的已知数。等式（1）根据“比的后项×比值=比的前项”可转化为xy=6(6一定)，说明x和y成反比例；等式（2）根据“一个因数=积÷另一个因数”可转化为n÷m=8，即n︰m=8(8一定)，说明n和m成正比例。看看，（1）中有比号，可两种量却成反比例关系；（2）中有乘号，可两种量偏偏成正比例关系。

处方（1）×（2）×