利用灭点进行相机检校与定姿的充要条件及其不确定性分析
2012-07-25李畅
李 畅
华中师范大学 城市与环境科学学院,湖北 武汉 430079
1 引 言
灭点是一种无成本的控制点,可用于非量测相机的定标(内方位元素:主距)及任意相机的定姿(外方位元素:角元素),在本文中将“定标”和“定姿”合称“定参”。以往的研究几乎都假定3个正交方向上灭点存在[1-5],然而有些场景中不存在3个正交方向灭点或者三灭点很难被全部检测出来,那么传统的三灭点定参理论在实际应用中受到了挑战。
另外,到目前为止,基于灭点的研究皆以应用研究为主,如灭点自动检测和基于灭点的相机定参方面[1,3-8],虽 然 精 度 评 定 必 不 可 少,却 都 是 以灭点为桥梁建立直线与相机参数的关系,绕过灭点探讨相机参数的精度,然而对灭点本身的误差及其对应的误差空间分布研究并不多。
鉴于此,本文将探讨灭点定参的充要条件,重点分析双正交灭点联合误差分布条件下,双灭点及第三灭点误差空间分布及其不确定性问题。
2 灭点定参的充要条件
在人类活动最频繁的城市,建筑物提供了大量的“空间平行线”。根据计算机视觉与摄影测量的灭点理论可知,空间的平行线在影像上的投影应当严格相交于一点[6]。不同场景中相交所成的灭点个数亦会不同。由于建筑立面的特殊性,通常只能检测出两个灭点:建筑物水平方向灭点X和铅垂线方向灭点Y,而垂直于建筑物(深度)方向的灭点Z不易被检测。值得注意的是,影像中灭点个数可能会出现大于3而正交方向的灭点数却小于3的情况,如图1(a)截面为正六边形的棱柱有4个灭点,但仅存在两个正交方向的灭点。图1(b)截面为正五边形的棱柱有6个灭点,也仅存在两个正交方向的灭点。
文献[9]论述了灭点个数对相机参数确定的影响。在此基础上,补充并给出灭点定参的充要条件如下:
(1)若存在3个正交方向的灭点,则可采用文献[9]中的定参方法。
(2)若仅存在两个正交方向的灭点,则需采用双灭点定参方法,即解算出第3个正交方向的灭点从而转化成三灭点定参问题。但存在一种病态情况(将在下一节讨论)。
(3)不存在正交方向的灭点,此时无解。
即灭点定参的充要条件为:当且仅当存在3个正交方向的灭点。综上可知,对于规则的房子等建筑物,出现3个正交方向上的灭点是可能的,但更一般的情况下,像方可能存在两个、3个、甚至多个方向上的灭点,但这些方向不一定都相互正交。加之灭点检测算法的灵敏性又会对检测到的灭点数打折扣(如,立面很难检测深度方向灭点),故双正交方向灭点更为普遍,亟须研究该条件下的灭点理论与方法并探讨其不确定性。
3 双正交灭点条件下的灭点问题
3.1 双灭点不确定性分析
文献[10]提出了3种确定地理信息数据中点的不确定方法:一是解析法,即基于统计学中的误差传播定律,其分布、方差协方差的传播;二是基于试验法;三是基于模拟法。
通过解析法分析灭点不确定性方法如下:在有噪声的情况下,空间平行线在影像上的投影未必交于一点,即存在闭合差。满足灭点方向分组的线段ij对应灭点V。
如图2,由i、j、V三点共线可得

式中,(xV,yV)为灭点V的坐标;(xi,yi)、(xj,yj)分别为点i、j坐标,线性化后矩阵方程为[11]

式中,观测向量为V=[vxivyivxjvyj]T;未知数(即灭点)为x=[vxvy]T;A为观测系数矩阵;B为未知数系数矩阵;W为闭合差。此为附有参数的条件平差模型,在平差时采用粗差探测的“选权迭代法”[12]可在计算灭点坐标的同时将不支持此灭点的粗差直线(误分组)剔除掉,得到灭点坐标。
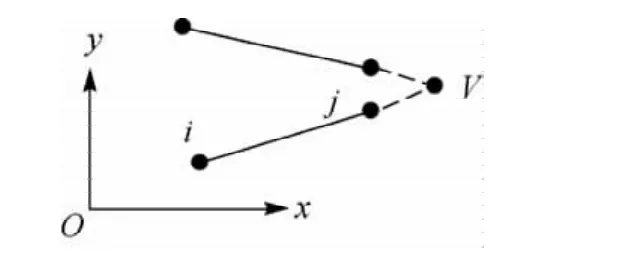
图2 灭点与分组直线段Fig.2 Vanishing point and grouped line segments
文献[4]提出如下指标评价灭点精度

式中,θi、θj表示交会灭点的两条直线各自的角度。显然指标c接近于1精度最高,当θi-θj为90°时,c=1,即当两直线正交时,灭点的精度最高。在平行摄影时,物方的平行直线在像方几乎也都是相互平行的。实际中c值往往很大,那么仅通过式(3)是无法更好评价灭点精度的,而且对灭点的点位误差,和任意方向上的位差都无法评定。所以可利用误差椭圆[11]来评定灭点分布的不确定性。
由平差中的协因数传播律可知式(1)对应未知参数(灭点)的方差为

则灭点的点位误差为

误差椭圆参数计算如下[13]
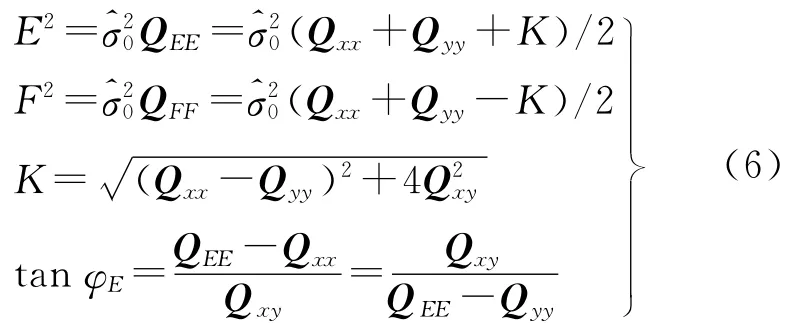
式中,QEE表示灭点在φE方向上取得位差的极大值;QFF为φE正交方向的极小值;E和F对应误差椭圆的长轴和短轴。此椭圆方程长轴对应的方位角为φE。根据点位误差椭圆可以解算出点位误差曲线从而确定任意方向上的误差。
然而,在工程应用中,有时需要关心任意两个待定点之间相对位置的精度,此时点位误差椭圆失效,需用相对误差椭圆进行估算。设两个待定点为Pi和Pk,这两点的相对位置可通过其坐标差来表示,即
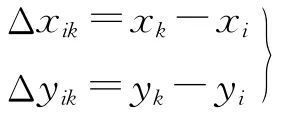
根据协因数传播律可得

由于灭点的平差都是基于直线段分组的,X方向的分组直线对应X方向的灭点,Y方向的分组直线对应Y方向的灭点,这两组观测值相互独立,所以其相关系数为零
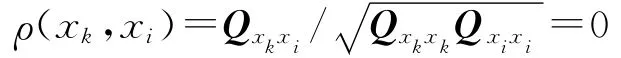
即式(7)中

可得计算Pi和Pk点间的相对误差椭圆3个参数[13]的公式

下面讨论式(8)中的如何确定。此时涉及两类独立观测值:X和Y方向灭点,依据灭点方程(2)可列出如下方程
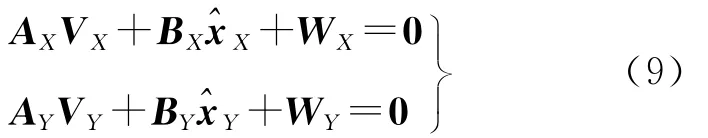
先对各类观测量定初权,进行预平差,灭点初始定权可参见文献[11]。再用平差后得到的观测值改正数进行估计并重新定权,如此重复,直到不同类观测值的权趋于合理,即采用赫尔默特(Helmert)验后方差分量估计[14],以此估算出单位权方差。
3.2 第三正交方向灭点解算
图3中3个正交方向的灭点为X∞,Y∞,Z∞即为三点透视,摄影中心为S,o为相机主点,f为主距,3个正交方向X、Y、Z的直线所形成的灭点必落在相应的坐标轴上。因此SX∞Y∞Z∞为一直角锥,So⊥ΔX∞Y∞Z∞,则相机主点o为ΔX∞Y∞Z∞的垂心[9]。
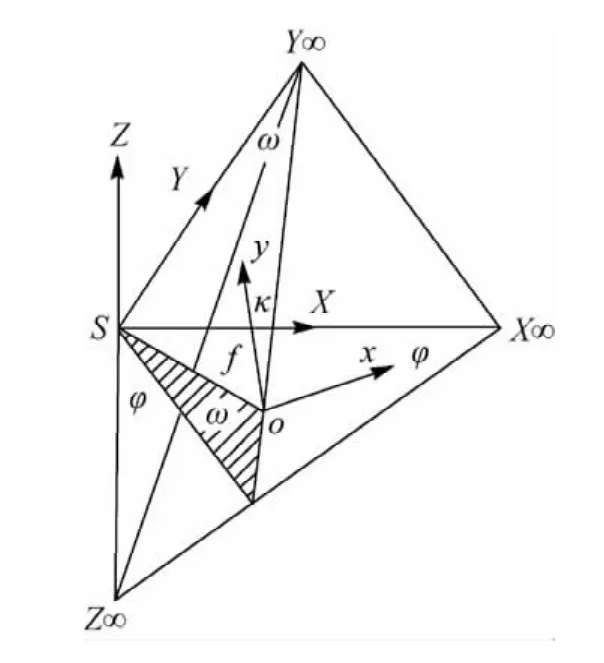
图3 三正交方向上灭点几何关系Fig.3 Image geometry with three vanishing points
设像主点坐标O(x0,y0)为坐标系原点,VX(x1,y1)、VY(x2,y2)和VZ(x3,y3)为该坐标系下三正交方向灭点坐标,并已知两个灭点VX和VY,以及O(x0,y0),如何解算第3个正交方向的灭点VZ?如图4,O(x0,y0)是像主点同时也是灭点三角形ΔVXVYVZ的垂心(注意不是重心,若为重心,灭点三角形在像主点为圆心的外接圆上,双灭点无法定参)。易知OZo⊥VXVY,VXOXo⊥VZVY,所以VZ是ZoO与VYXo的交点,可得方程

解得第三灭点坐标VZ(x3,y3)

式中

灭点VX、VY的误差椭圆方程可写为

式中,E和F由式(6)计算可得,将式(13)转换到像主点为原点的坐标系,则有

将其代入椭圆式(13),可得

此方程就是在右手坐标系XOY(见图4)下灭点VX,VY的误差椭圆方程,由此也可确定XOY坐标系下相对误差椭圆方程。式(14)中i=1,2,即为XOY下VX和VY椭圆圆心坐标。

图4 灭点几何及误差椭圆Fig.4 Vanishing points geometry and error ellipses
值得注意式(11)存在一种病态情况,即

将式(12)代入式(15)可得

也就是当两个灭点坐标VX、VY与像主点坐标O(x0,y0)3点共线时,不能解算第3个正交方向灭点,因此无法通过灭点定参。
3.3 第三灭点不确定性随机统计模拟
3.3.1 第三灭点不确定空间分布模拟
上面讨论了如何通过两个正交方向灭点坐标VX和VY解算第3个正交方向灭点坐标VZ的方法,然而灭点VX和VY本身就存在不确定性。文献[10]用点的标准椭圆和圆形正态模型分析了点误差的不确定性。在点误差的二维正态分布下还可以计算其概率[13]。所以,本节提出在双灭点联合误差分布(误差椭圆)条件下,利用 Monte-Carlo方法模拟第三灭点的误差分布。算法如下。
(1)在误差椭圆内生成均匀分布的伪随机点:
①在VX和VY对应误差椭圆的外切矩形区域内生成均匀分布随机点;
②通过下面的两个集合判断是否落入VX或VY误差椭圆内

即保留落入误差椭圆内的均匀分布随机点。
(2)遍历VX和VY误差椭圆内的随机点并利用推导的第三灭点坐标公式(11)计算对应的Z方向灭点,模拟出VZ的离散点空间分布。
3.3.2 第三灭点空间分布面积估算
如图5要计算y=f(x)与x=0和y=0围成的Ω区域面积,通常可以通过积分的方法。

图5 基于Monte-Carlo估算Ω区域面积Fig.5 Estimation of the area size ofΩ
此处可通过Monte-Carlo方法来计算,根据几何概型可知落入Ω区域的概率为

式中,p为概率;S_AreaΩ为所求面积;nΩ为落入Ω的随机点数;N为总随机点数
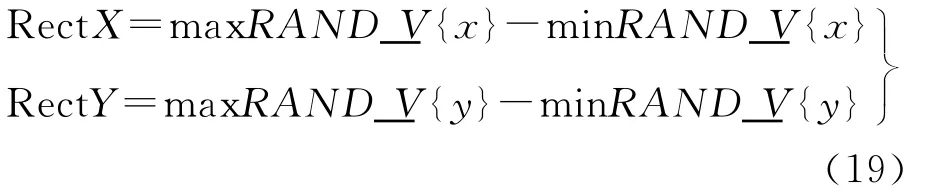
RectX和RectY为Ω的外切矩形区域的长和宽,乘积即为Ω的外切矩形区域面积。图5中RectX=RectY=1。由中心极限定理可知当N趋于无穷时有
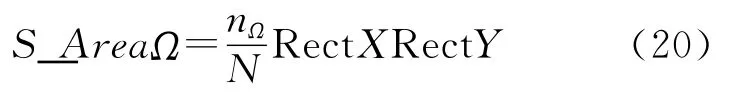
4 试 验
4.1 模拟试验
表1中设计了4组误差椭圆参数进行仿真试验。

表1 误差椭圆参数Tab.1 The error ellipse parameters of VXand VY
根据表1中第1组误差椭圆参数并忽略相机的畸变,令像主点坐标为(0,0)(随着当代相机镜头的畸变越来越小,此处做一个近似)。模拟出的第3个正交方向灭点的分布如图6所示,其中类似双叶型的VZ区域即为Z方向灭点的不确定性空间分布。在此区域的外切矩形内随机投15 000个点,并统计落入VZ区域的点数并根据式(20)计算得VZ区域面积S_AreaVZ为1 447.1像素,该面积区域的估算精度约为±0.008像素。第2组数据在第1组的基础上减少了VY分布范围显然S_AreaVZ减少了。第3组数据在第2组的基础上增大VX面积的同时增大了VX和VY间的距离,S_AreaVZ虽然变大但仍小于第1组数据中VZ区域的面积。第4组数据在第3组的基础上进一步增大了VX和VY间的距离,并令VX的误差椭圆长短半轴与VY相同,此时VZ区域的面积为3 933.8,不确定性最强。但如果在第4组的基础上将VY恢复到原来的长短半轴长,不确定性降到了5组数据中的最低。由此有理由假设:在VX和VY的空间分布范围一大一小的条件下,随着两者间的距离增大,VZ分布的不确定性会降低。
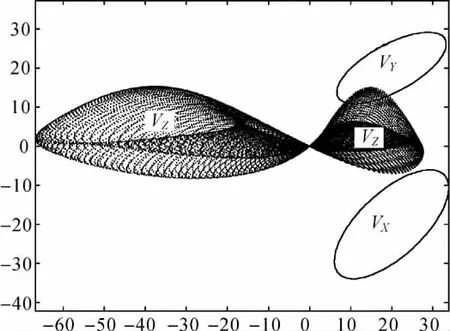
图6 灭点VZ空间分布Fig.6 VZerror graph under the Vxand Vy
4.2 影像试验
为了验证上述假设进行实拍检验,相机为KODAR (PROFESSIONAL DCS Pro SLR/n)普通数码相机,像幅大小1000像素×1500像素,相机主距24mm,像元大小0.025mm,影像见图7。提取图7中的直线段,并对VX和VY灭点方向线段进行分组,采用式(2)可计算出灭点坐标。忽略相机系统误差,假设像主点坐标为(0,0),由式(6)和式(8)可得双正交方向灭点的误差椭圆和相对误差椭圆,再根据VX和VY坐标及其误差椭圆内生成的均匀分布随机点和式(11)估算出第3个正交方向灭点的坐标及分布范围(xmin,ymin,xmax,ymax表示VZ空间分布的边界坐标最大最小值)见表2。利用 Monte-Carlo方法在VZ外切矩形内随机投15 000个随机点,再用式(20)估算出VZ分布的面积为28.2±0.008(像素)。由此看出,尽管VX的误差分布面积较大,但在VY分布面积不太大且VX和VY间距很大的条件下,它们的联合误差分布VZ的不确定区域却相对较小。由此,验证了前面的假设,其他实拍影像也能得出一致结论。此结论对于基于双灭点的相机定参十分重要,拍摄角度对灭点的精度有很大的影响,获得较好精度的双灭点拍摄角度未必能得到(三灭点更难),但拍摄获得一个较好精度的灭点角度比较容易,如图7仰拍时VY灭点不确定性较小,表2中VY的误差椭圆长轴和短轴皆相对较小。而且一般物方平行线投影于像方交会出的灭点间的坐标距离往往又很大,这都符合假定条件:在VX和VY的空间分布范围一大一小的条件下,随着两者间的距离增大,VZ分布的不确定性似乎会变小。

图7 原始影像及直线提取灭点分组后影像Fig.7 Original image and extracted and grouped lines

表2 双灭点及第三灭点的不确定性Tab.2 The error ellipse parameters of VXand VYfor figure 7
5 结 论
本文在原来灭点理论与方法的基础上,补充完善了灭点检校与定姿的充要条件,给出了双正交方向灭点定参中存在的病态问题。补充了基于双灭点(两个待定点)的相对误差椭圆评定相对精度的方法。重点探讨了在更普遍的情况:双正交方向灭点联合误差椭圆分布条件下,解算第3个正交方向灭点坐标并随机模拟其误差空间分布和不确定性问题。通过试验,提出并验证了第3灭点不确定性较小的条件,进一步揭示和探讨了灭点空间分布的规律。今后将通过计算灭点误差空间分布的解析解,进一步揭示和论证灭点的不确定性规律。
[1] MAHZAD K,FRANCK J.Precise,Automatic and Fast Method for Vanishing Point Detection[J].The Photogrammetric Record,2009,24(127):246-263.
[2] ZHANG Zuxun,ZHANG Jianqing.Generalized Point Photogrammetry and Its Application[J].Geomatics and Information Science of Wuhan University,2005,30(1):1-5.(张祖勋,张剑清.广义点摄影测量及其应用[J].武汉大学学报:信息科学版,2005,30(1):1-5.)
[3] HEUVEL F A.Automation in Architectural Photogrammetry:Line-photogrammetry for the Reconstruction from Single and Multiple Images[D].Delft:Netherlands Geodetic Commission,2003.
[4] CAPRILE B,TORRE V.Using Vanishing Points for Camera Calibration[J].International Journal of Computer Vision,1990,4(2):127-140.
[5] LAZAROS G,GEORGE K,PETSA E.An Automatic Approach for Camera Calibration from Vanishing Points[J].ISPRS Journal of Photogrammetry and Remote Sensing,2007,62(1):64-76.
[6] ZHANG Zuxun,Zhang Yong.Study of the Vertical Lines Supported Aerial Triangulation over Urban Areas[J].Geomatics and Information Science of Wuhan University,2007,32(8):659-662.(张祖勋,张勇.城区铅垂线辅助空中三角测量研究[J].武汉大学学报:信息科学版,2007,32(8):659-662.)
[7] XIE Wenhan,ZHANG Zuxun.Camera Calibration Based on Vanishing Points of Multi-image[J].Acta Geodaetica et Cartographica Sinica,2004,33(4):335-340.(谢文寒,张祖勋.基于多像灭点的相机定标[J].测绘学报,2004,33(4):335-340.)
[8] SHUFELT J A.Performance Evaluation and Analysis of Vanishing Point Detection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1999,21(3):282-288.
[9] ZHANG Zuxun,WU Jun,ZHENG Jianqing.A Method for Determining Orientation Parameters in Image-based Reconstruction of Architectural Scenes[J].Geomatics and Information Science of Wuhan University,2003,32(8):265-300.(张祖勋,吴军,张剑清.建筑场景三维重建中影像方位元素的获取方法[J].武汉大学学报:信息科学版,2003,32(8):265-300.)
[10] SHI Wenzhong.Theory and Methods for Handling Errors in Spatial Data[M].Beijing:Science Press,2000.(史文中.空间数据误差处理的理论与方法[M].北京:科学出版社,2000.)
[11] LI Chang,ZHANG Zuxun,ZHANG Yongjun.Evaluating on the Theoretical Accuracy of Error Distribution of Vanishing Points[J].Acta Geodaetica et Cartographica Sinica,2011,40(3):393-396.(李畅,张祖勋,张永军.灭点误差分布的理论精度评定[J].测绘学报.2011,40(3):393-396.)
[12] LI Deren,YUAN Xiuxiao.Error Processing and Reliability Theory[M].Wuhan:Wuhan University Press,2002.(李德仁,袁修孝.误差处理与可靠性理论[M].武汉:武汉大学出版社,2002.)
[13] Subject Group of Survey Adjustment of School of Geodesy and Geomatics of Wuhan University.Error Theory and Foundation of Surveying Adjustment[M].Wuhan:Wuhan University Press,2003.(武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉:武汉大学出版社,2003.)
[14] CUI Xizhang,YU Zongchou,TAO Benzao,et al.Generalized Surveying Adjustment(Second Edition)[M].Wuhan:Wuhan University Press,2009.(崔希璋,於宗俦,陶本藻,等.广义测量平差:第2版[M].武汉:武汉大学出版社,2009.)
[15] ROBERT C P,CASELLA G.Monte Carlo Statistical Methods:2nd ed[M].New York:Springer-Verlag,2004.
