针对流密码HC-256'的区分攻击

李顺波 胡予濮 王 艳

(西安电子科技大学计算机网络与信息安全教育部重点实验室 西安 710071）

1 引言

为进一步推进流密码的研究，2004年欧洲启动了eSTREAM计划[1]，主要任务是征集安全快速的流密码算法，至2005年4月，共征集到34个候选算法。HC-256[2]和HC-128[3]都是基于表驱动的候选流密码算法，由于其运行速度快、安全性能高，至今未见有效的分析方法。为了避免从系统内部恢复出初始密钥，文献[2]设计了HC-256的改进算法——

HC-256'，其内部状态P和Q每运行一步就交替更新一次，具有更高的安全性；还未发现任何关于HC-256'的分析结果，其安全性分析已经成为一个热点问题。

文献[4]利用线性逼近区分攻击对流密码HC-256进行了安全性分析，需要约279.82 bit的密钥流字节就可以把密钥流序列和随机序列区分；然而对HC-256的改进算法HC-256'能否利用区分攻击进行安全性分析是一个有意义的研究课题。本文提出了一种针对流密码HC-256′的线性区分攻击。首先利用假设检验给出了区分优势的计算公式；然后，对偶数位置上的输出序列字节利用不同的非线性函数表示不同的内部状态更新函数，在最低位比特通过线性逼近构建几乎最优区分器。结果表明，需要约 2281bit就能以0.9545的区分优势将HC-256'的密钥流序列和随机序列区分开。

2 基础知识

2.1 区分攻击

区分攻击[5](distinguishing attack)是一种灵活有效的密码分析方法，2002年由Coppersmith等人提出，其基本思想是通过观察某些输入与输出比特之间的关系来判别这些比特是来自真随机源还是来自密码，将其转化为一个假设检验问题。尽管从攻击结果上看，区分攻击是最弱的，但面对区分攻击，密码设计者往往很难做到疏而不漏。因此区分攻击已经成为判定密码性质好坏的一个严格的安全标准。许多流密码算法都遭到区分攻击的威胁，如Shannon[6,7], SN3[8]和 RC4[9,10]等。

区分攻击的关键是寻找适当的区分器，更具体地说，区分器是指区分一串密钥流和一串真正随机序列的一种有效算法，且以密钥流的某些弱点为基础，而正是这些弱点体现了给定的密钥流具有的不随机性。区分器就是利用这些弱点来设计算法的。

一个区分器D将密钥流生成器与随机生成器区分开的成功性称为区分优势(或成功概率)，由以下两个概率决定：

(1)当所给序列来自于密钥流生成器时，回答为“密钥流序列”的概率P0(D)；

(2)当所给序列来自于随机生成器时，回答为“密钥流序列”的概率P1(D)。

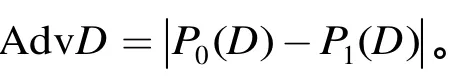
定义2[7]设Pr(D)为一个逼近D成立的概率，则偏差e= 2 Pr(D)- 1，即Pr(D) = ( 1/2)(1 +e)。

2.2 假设检验

设原假设H0：序列X来自密钥流生成器，即PX=P0(zi)；

备择假设H1：序列X来自随机生成器，即PX=P1(zi)。

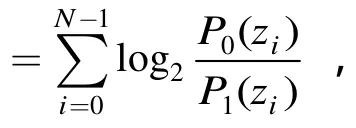
区分攻击算法

输入：Nbit序列 (z0,z1,… ,zN-1)

输出：序列来自随机序列还是密钥生成序列

(2)如果LLR≥0，输出“序列来自密码”，

否则，输出“序列来自随机序列”。

由于统计量D(zi) ∈ { 0,1}服从二项分布，且是独立同分布的随机变量。当N无限增大时，利用中心极限定理，该二项分布无限趋于标准正态分布，

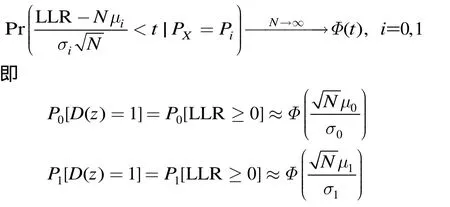
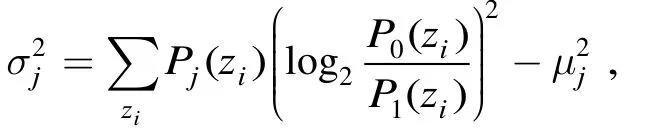
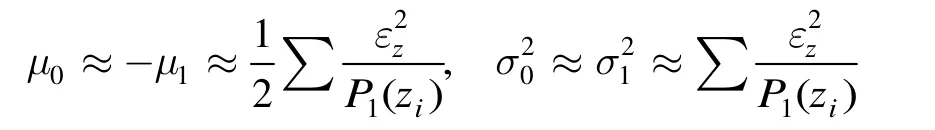
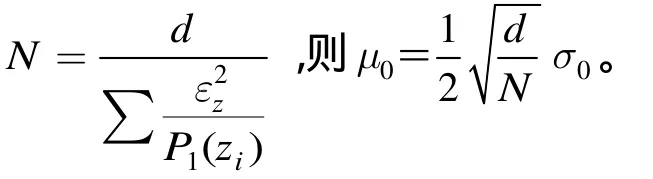
所以

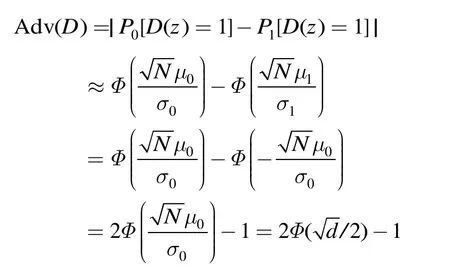
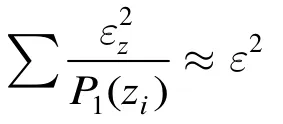
表1 P j ( zi )和εz的取值

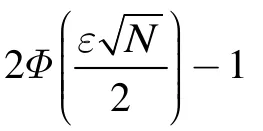
引理1[2]设H是mbit输入nbit输出的S-盒，且m≥n。若x1,x2是H的两个随机mbit输入，则Pr[H(x1) =H(x2)]= 2-m+ 2-n- 2-m-n。

3 流密码HC-256′

流密码HC-256'是HC-256的改进算法，都是文献[2]中提出的面向软件实现的快速同步流密码，256 bit密钥(K)和256 bit初始化向量(IV)，内部状态P和Q都为1024 bit。HC-256'借鉴了RC4的思想，同时引入了面向字节的非线性函数来更新系统的内部状态，运行速度很快，具有更高的安全性。其初始化和非线性函数都和 HC-256是一样的；但唯一的差别在于密钥流生成算法。HC-256的密钥流生成算法是连续运行1024步更新一次状态P，再连续运行1024步更新另一个状态Q。而HC-256'的密钥流生成算法是内部状态P和Q每运行一步就需要更新一次。具体算法如3.1节-3.3节所述。

3.1 运算符号

流密码HC-256'中的运算符号标注如下：

+：x+y表示x+ym od232；

>> ：右平移算子，x＞＞n表示x向右平移nbit；

>>> ：右循环算子，x＞＞＞n表示x向右循环移动nbit，即(x＞＞n) ⊕ (x＜＜ ( 32 -n)), 0≤n＜ 3 2。

3.2 密钥初始化

密钥初始化过程中，内部状态是密钥和初始化向量的级联，256 bit的密钥和初始化向量被分为8个32 bit的字，记为：K=K0||K1||… ||K7和IV=IV0||IV1||… ||IV7。将密钥和初始化向量扩展到2560个数组Wi(0 ≤i≤2559)

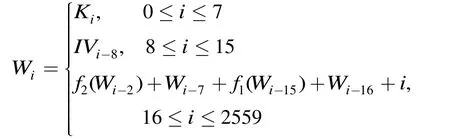
其中

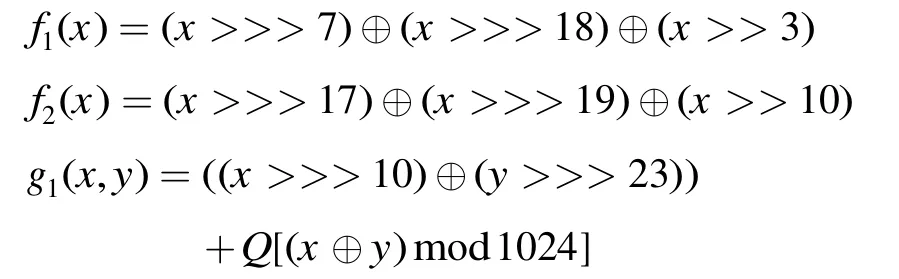
其中h1,h2表示32 bit输入和32 bit输出的S盒，32 bit字x=x3||x2||x1||x0中x0表示x的最低位字节(least significant bit)，x3表示x的最高位字节(most significant bit)。

两数组P和Q表示32 bit内部状态，分别为：P[i]=Wi+512,Q[i]=Wi+1536, 0 ≤i≤ 1 023。

3.3 密钥流生成器

初始化4096步后输出密钥流比特si，生成的密钥流长度为 2128bit；其算法如下：

4 区分攻击HC-256′

本节利用区分攻击分析流密码HC-256'的安全性，关键是寻找HC-256'密钥流生成器的弱点，而其困难在于内部状态P和Q每运行一步就要更新一次，P和Q更新时的非线性函数是不同的。本文提出了一种新的区分攻击思想，把问题转化为判断在偶数(奇数)位置上的输出序列是来自密钥流序列还是随机序列。利用不同的非线性函数来表示不同的内部状态更新函数，旨在讨论在最低位比特状态P和密钥流s2i的弱点。

已知在偶数位置上的密钥流输出算法为

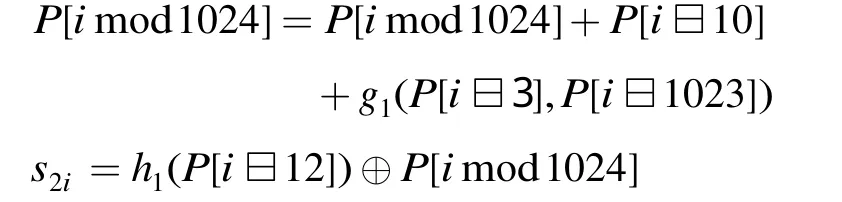
当10 ≤(imod1024) ＜ 1 023时，记zi=P[i12]为32 bit字，P[im od1024]=s2i⊕h1(zi)，所以P[i10]=P[(i- 1 0)mod1024]=。同理，

因此在偶数位置上的反馈函数可以写成如下形式：

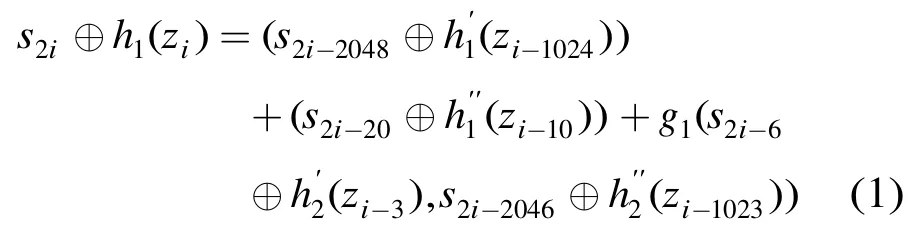
对于模 232加法，直接把式(1)的密钥流序列区分开是非常困难的。但值得注意的是，在最低位比特，运算‘+’和‘⊕’是一样的。因此，利用函数g1(x)，在最低位比特式(1)可以写成下列形式：

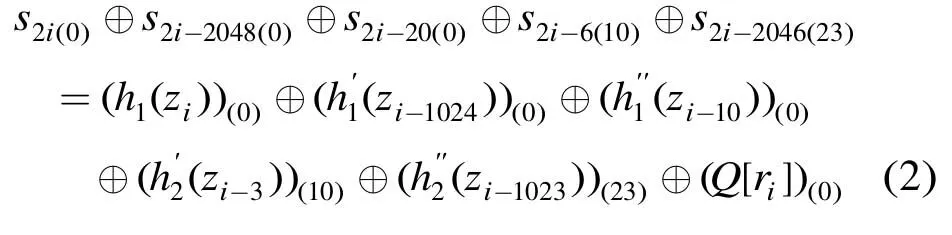
同理，当1024 ·a+ 1 0 ≤i,j＜ 1 024 ·a+ 1 023，且i≠j时有

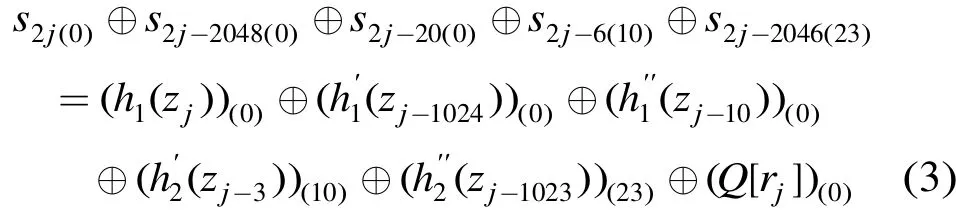
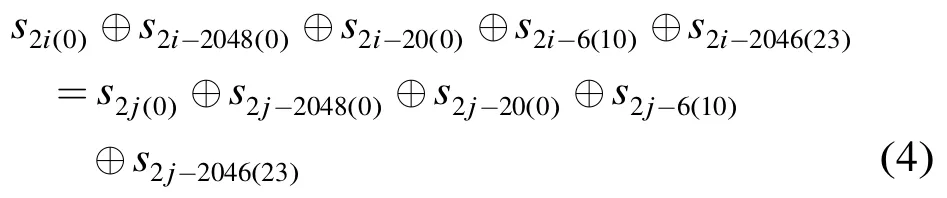
等价于下面等式成立：

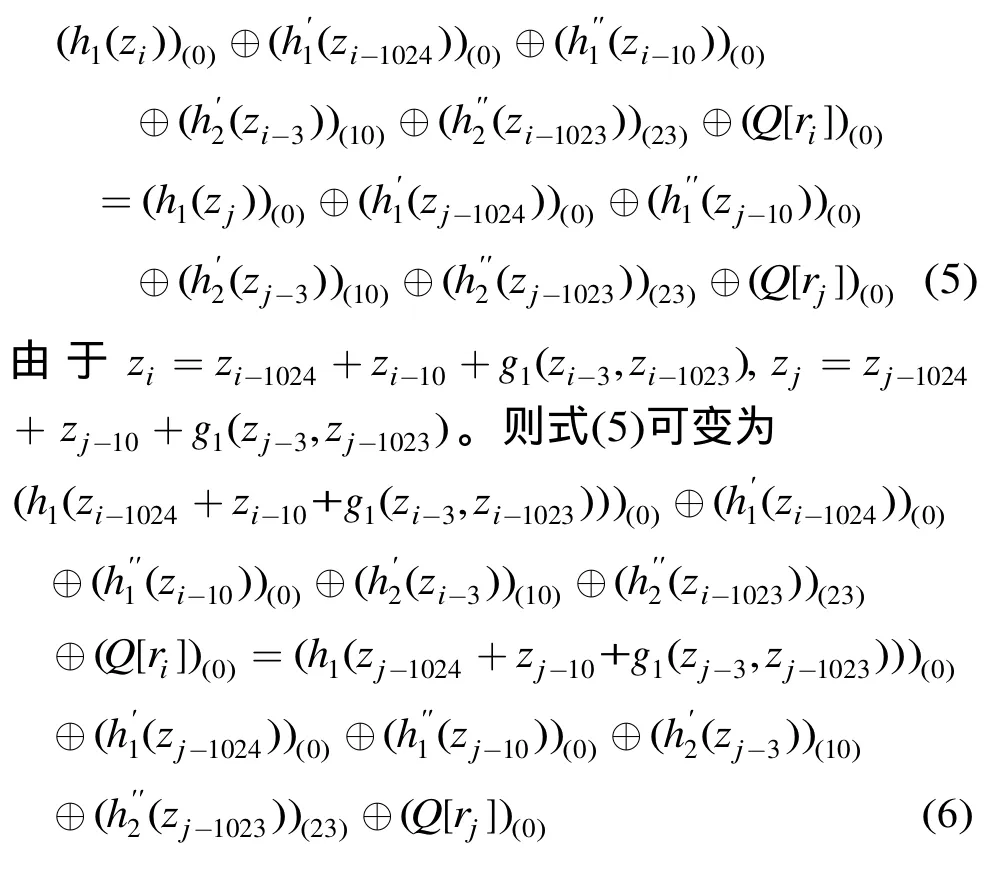
根据上述推理，式(4)就是我们构造的区分器。式(4)成立的概率等价于式(6)成立的概率。而式(6)左边含有138 bit变量zi-3,zi-10,zi-1023,zi-1024和ri，记x1=zi-3||zi-10||zi-1023||zi-1024||ri。式(6)右边也含有138 bit变量zj-3,zj-10,zj-1023,zj-1024和rj；记为x2=zj-3||zj-10||zj-1023||zj-1024||rj。我们可以将式(6)两边看作两个S-盒函数，要使得式(6)成立，就要满足以 138 bit为变量的两个 S-盒相等，即H(x1)=H(x2)。其中H表示随机选择的138 bit输入-1 bit输出的 S-盒。利用引理 1，式(6)成立的概率为1/2 + 2-139。

因此，区分器式(4)成立的概率为p=1/2+ 2-139= ( 1/2)(1 + 2-138)。所以该区分器的偏差为e= 2-138。利用定理1，当密钥流比特N=e-2=2276时，该区分攻击的区分优势为 0.3928；当N=16·e-2= 2280时，该攻击以 0.9545的区分优势把密钥流序列和随机序列区分开。

然而，该区分攻击只讨论了在偶数位置上HC-256'的安全性，用同样的方法可以分析在奇数位置上的安全性。综上所述，需要约 2 ·N=2281bit密钥流就能以0.9545的区分优势把流密码HC-256'与随机序列区分开。

5 结束语

本文利用线性区分攻击分析了流密码HC-256'的安全性，通过线性逼近内部状态寻找密钥流生成器的弱点建立区分器，区分密钥流序列和随机序列需要约 2281bit；且该攻击的区分优势为0.9545。虽然该结果超过了密钥流序列的长度，但从理论上回答了2009年Sekar等人提出的开放问题。然而，近年来对HC-256的简化算法HC-128的研究仅限于文献[14-17]，能否利用区分攻击对流密码 HC-128进行有效的安全性分析仍然是一个有意义的问题，值得做进一步研究。

[1]eSTREAM—the Ecrypt Stream Cipher Project[EB]. http://www.ecrypt.eu.org /stream/, 2005.

[2]Wu Hong-jun. A new stream cipher HC-256[C]. FSE 2004,New Delhi, India, 2004, 3017: 524-538.

[3]Wu Hong-jun. The stream cipher HC-128[C]. New Stream Cipher Designs, 2008, 4986: 39-47.

[4]Sekar G and Preneel B. Improved distinguishing attacks on HC-256[C]. IWSEC 2009, Toyama, Japan, 2009, 5824: 38-52.

[5]Coppersmith D, Halevi S, and Jutla C. Cryptanalysis of stream ciphers with linear masking[C]. CRYPTO 2002, Santa Barbara, California, 2002, 2442: 515-532.

[6]Ahmadian Z, Mohajeri J, Salmasizadeh M,et al.. A practical distinguisher for the Shannon cipher[J].The Journal of Systems and Software, 2010, 83(4): 543-547.

[7]常亚勤, 金晨辉. 对Shannon算法的线性区分攻击[J]. 电子与信息学报, 2011, 33(1): 190-193.

Chang Ya-qin and Jin Chen-hui. Linear distinguishing attack on Shannon algorithm[J].Journal of Electronics&Information Technology, 2011, 33(1): 190-193.

[8]Keller N and Miller S D. Distinguishing attack on stream ciphers based on arrays of pseudo-random words[J].Information Processing Letters, 2010, 110(4): 129-132.

[9]Maitra S, Paul G, and Gupta S. Attack on broadcast RC4 revisited[C]. FSE 2011, Lyngby, Denmark, 2011, 6733:199-217.

[10]Sepehrdad P, Vaudenay S, and Vuagnoux M. Statistical attack on RC4 distinguishing WPA[C]. EUROCRYPT 2011,Tallinn, 2011, 6632: 343-363.

[11]Baigneres T, Junod P, and Vandenay S. How far can we go beyond linear cryptanalysis[C]. Asiacrypt 2004, Jeju Island,Korea, 2004, 3329: 432-450.

[12]Hell M, Johansson T, and Brynielsson L. An overview of distinguishing attacks on stream ciphers[J].Cryptography and Communications, 2009, 1(1): 71-94.

[13]Crowley P. Improved cryptanalysis of Py[C]. Workshop on the State of the Art of Stream Ciphers (SASC 2006), Leuven,Belgium, 2006: 52-60.

[14]Liu Yun-yi and Qin Tuan-fa. The key and IV setup of the stream ciphers HC-256 and HC-128[C]. Networks Security,Wireless Communications and Trusted Computing, Wuhan,IEEE, 2009: 430-433.

[15]Maitra S, Paul G, and Raizada S. Some observations on HC-128[J].Designs, Codes and Cryptography, 2010, 57(3):1-15.

[16]Kircanski A and Youssef A M. Differential fault analysis of HC-128[C]. Africrypt 2010, South Africa, 2010, 6055:261-278.

[17]Paul G, Maitra S, and Raizada S. A combinatorial analysis of HC-128[R]. Cryptology ePrint Archive, Report 2010/387,2010.