小型风力发电系统控制策略的研究
2012-07-25方宁
方宁
(湖南铁道职业技术学院电气工程系,湖南 株洲 412001)
1 引言
近年来,小型风力发电机组推广应用范围不断扩大。除了传统的广大农牧区用户应用小型风力发电机组照明看电视以外,由于汽油、柴油价格飞涨,且供应渠道不畅通,内陆、江湖、渔船、边防哨所、部队、气象、微波站等使用柴油发电的用户,逐步改用风力发电或风光互补发电。此外,生态环保公园、林荫小道、别墅庭院等地方,也购买安装小型风力发电机,作为景观,供人们休闲欣赏[1]。本文对小型风力发电机的三种控制策略进行了研究。
2 能量优化管理集成控制策略[2]
2.1 系统构成
独立运行的小型风力发电系统一般包括能量产生环节、能量存储环节、能量消耗环节3部分。该系统采用定桨距风力机直接耦合永磁同步发电机方式,在二极管整流桥和蓄电池之间插入DC/DC变换器实现能量控制。整个系统不使用测风速装置,发电机转速根据输出交流电压的频率或幅值与转速之间对应关系测量。风力机超速保护采用机械折尾翼限速与电气耗能电阻限速相结合方式,从而简化系统结构,降低成本,提高运行可靠性。
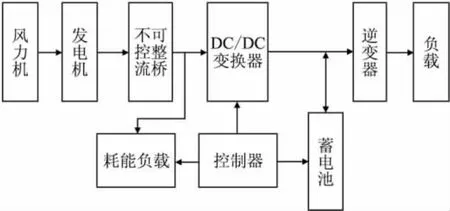
图1 小型风力发电机结构
2.2 能量流动分析
小型风力发电系统中风力机捕获能量的传递方向始终是单向的,而发电机输出电能的流向根据外电路的变化有不同的方向。蓄电池的能量流动为两个方向,依据外电路的不同可以工作在充电或放电状态,蓄电池的充电和放电过程根据负载情况的不同随机进行动态调节。由于风能和负载的随机性,为最大限度地利用风能及保证蓄电池的合理工作状态,集成控制方案将根据系统的工作状态,合理调度能量流动。系统运行时,风力发电机输出功率PE、负载消耗功率PL和蓄电池可以接受的充电功率PB,三者之间关系及相应的控制模式见表1。
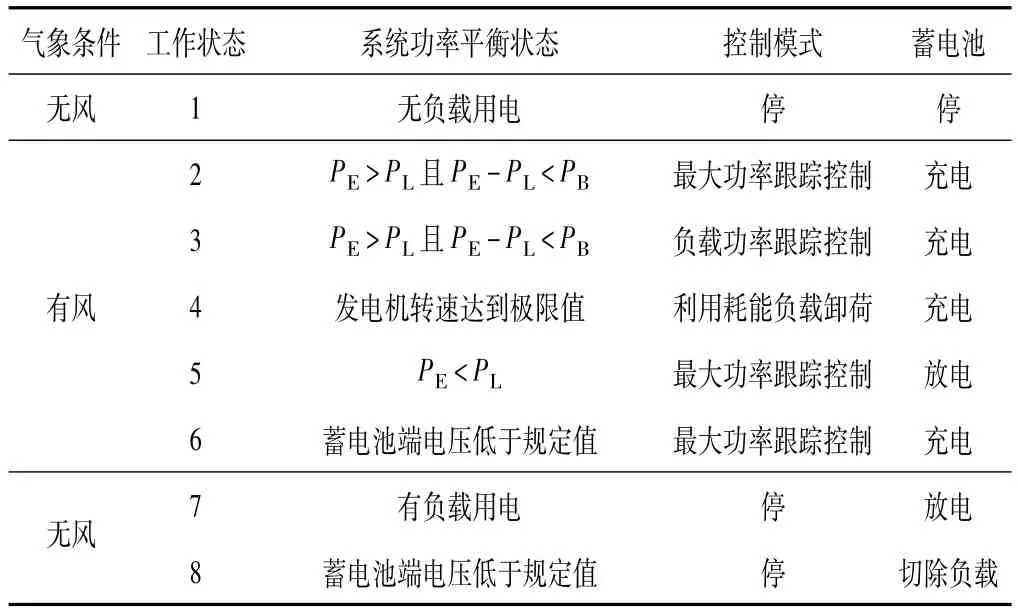
表1 小型风力发电机能量流动关系
2.3 工作状态转换
随着风速和负载不断变化,上述8种工作状态之间相互转换,通过检测对应的电压和电流可判断系统所处的工作状态,图2给出了小型风力发电系统的工作状态转换关系。由于工作状态转换是在能量合理调度的基础上完成的,而工作状态又包含最大功率跟踪控制、负载跟踪控制、蓄电池充放电控制及发电机超速保护控制等控制模式,该能量优化管理集成控制方案可以提高系统能量转换效率及改善蓄电池的工作状况,从而实现小型风力发电系统的优化及可靠性运行。
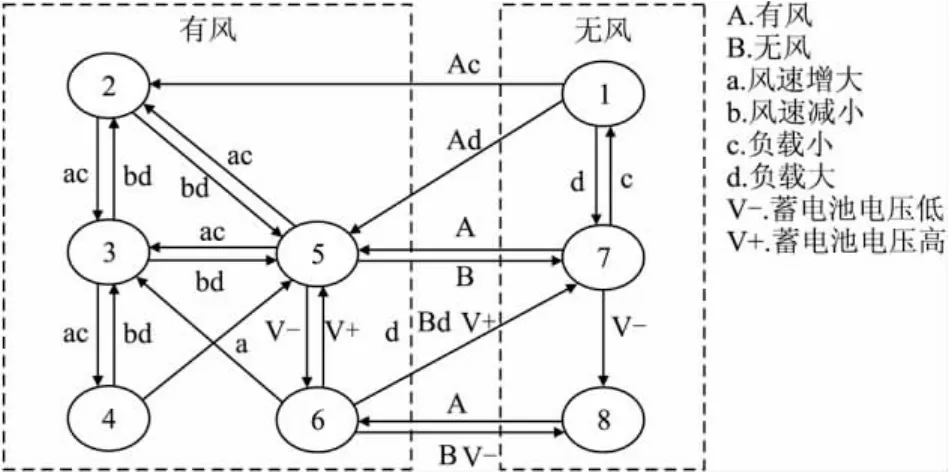
图2 小型风力发电机工作状态转换图
3 最大功率控制的扰动法[3]
由于风机系统中蓄电池和电容的存在,使蓄电池输出电压基本保持恒定,因此调节斩波器输出电流就实现了对永磁发电机电磁功率的调节,斩波器具有变换阻抗的作用,通过控制斩波器的占空比,可以调节斩波器的输入电阻,实现发电机输入、输出特性与负载阻抗相匹配,使发电机工作在最佳工作点,从而控制风力机转速,实现最大功率输出。
风力发电机的输出特性曲线如图3所示,从图中可以看出,最大功率的连线(点划线)将曲线族分为A和B两部分,最大功率控制扰动法的基本思想是:在系统中注入小幅正弦波信号,此信号和控制器输出进行叠加,形成斩波器控制信号;控制器输出是通过在正弦波信号的极大点和极小点时刻分别对输出电流采样,利用采样值差的积分产生的。
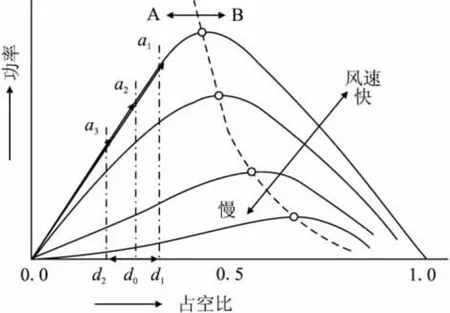
图3 小型风机的输出特性
最大功率控制扰动法的基本原理如图4所示,设正弦波扰动信号的幅值为dm,角频率为ω,当系统工作A区时,假定系统工作在a0点,其对应的占空比为d0,正弦波信号产生的扰动量在d1和d2之间连续变化,则此时瞬时占空比d为:
d=d0+dmsin(ωt)
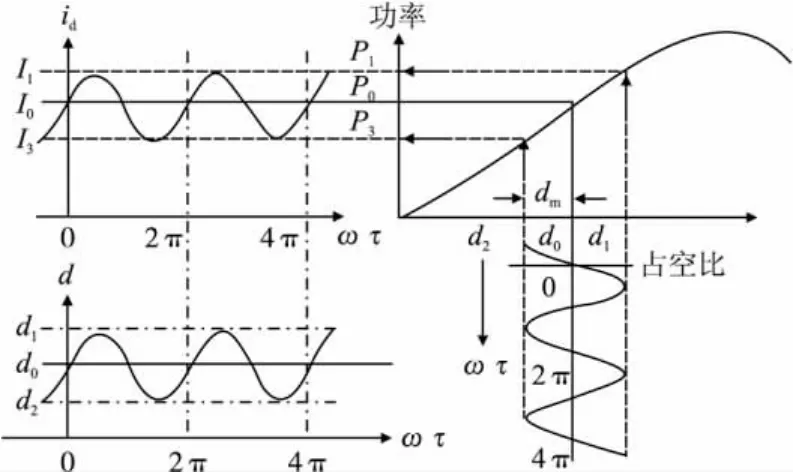
图4 最大功率扰动法控制原理
在输出电压恒定时,输出功率与输出电流成正比,当测得来自电流检测回路的电流时,d0由下式决定:
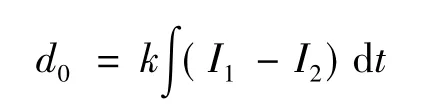
系统工作在A区时,随着占空比的增大,系统输出功率增大,此时的占空比d应向顶点方向增大。当系统工作在B区时,随着占空比的增大,系统输出功率减小,此时的占空比d应向顶点方向减小。
当测得来自电流检测回路的电流I1=I2时,Δd=0,这时占空比稳定在最大点上。当系统达到最大点时,输出电流和扰动信号之间的相位差为90°。利用小信号扰动法可实现系统平均功率达到最大值,而且方法简单,易于实现。
4 三点比较法控制
三点比较算法在跟踪稳定性方面是对固定步长的爬山算法和变步长算法的一种结合和改进。由于风力发电系统P—D曲线的单峰性及占空比调整步长值ΔD较小,我们在风力发电系统P—D曲线峰值点附近从左到右依次取三个点,(D1,P1),(D2,P2),(D3,P3)分别对应各工作点的占空比和功率。设D2为初始最大负载功率点对应的占空比值Dmax,DD是一个预先设定的用于占空比步长调整的常量。于是我们会得到如图5~图7所示的情形:
(1)当P1<P2且P2≤P3时,MPPT控制单元执行
{D2=D3;D1=D2-ΔD;D3=D2+ΔD},如图5所示。
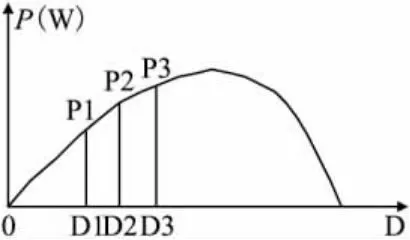
图5 当P1<P2且P2≤P3的情况
(2)当P1<P2且P2>P3时,MPPT控制单元执行
{ΔD=ΔD-DD;D1=D2-ΔD;D3=D2+ΔD},如图6所示。
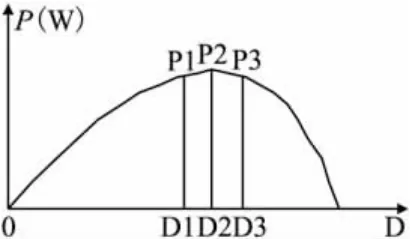
图6 当P1<P2且P2>P3的情况
(3)当P1≥P2且P2>P3时,MPPT控制单元执行
{D2=D1;D1=D2-ΔD;D3=D2+ΔD},如图7所示。
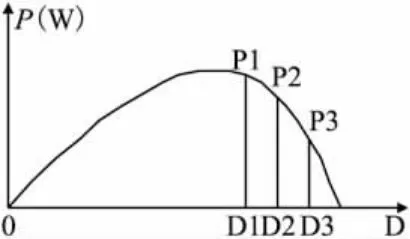
图7 当P1≥P2且P2>P3的情况
这种算法在第一种情况和第三种情况时,也即第二工作点的功率值P2离当前风速下对应的负载两端最大功率值点Pmax较远时,我们采用类似于爬山算法的固定步长扰动,使工作点功率值能够快速地接近最大功率值点,提高系统响应的快速性;当第二工作点功率值较为接近当前风速下对应的负载两端最大功率值点Pmax时,我们采用类似于变步长算法的变步长扰动,使工作点功率值能够更加精确细致地接近最大功率值点,从而满足系统精度的要求。
5 结束语
小型风力发电系统作为农村能源的组成部分,它的推广应用对于改善用电结构,特别是边远山区的生产、生活用能,推动生态环境建设诸领域的发展将发挥积极作用,因此具有广阔的市场前景。风能具有随机性和不确定性,风力发电系统是一个复杂系统。简化小型风力发电系统的结构、降低成本、提高可靠性及实现系统优化运行,对于小型风力风力发电系统的推广具有非常重要意义。
[1]叶杭冶.风力发电机组的控制技术[M].北京,机械工业出版社,2002.
[2]齐志远.小型风力发电系统能量管理集成控制的研究[D].内蒙古:内蒙古工业大学,2009.
[3]翁翔羿,张曦煌.小型风力发电系统风速追踪策略的仿真研究[J].计算机仿真,2011,28(5):328 -332.
