改进DE与广义神经网络在变压器故障诊断中的仿真研究

2012-07-25杨有婵黄哲周惠龙

电气开关 2012年5期

杨有婵，黄哲，周惠龙

(广西大学电气工程学院，广西南宁 530004)

1 引言

电力变压器作为电力系统中的关键电力设备，随着电网向智能化发展及对供电可靠性的要求不断提高，在线监测变压器故障在当前保证电网稳定方面显得尤为关键，可以及时发现变压器内部潜在故障，从而避免故障发展。油中溶解气体分析法(DGA)方法是目前工程及理论分析中最常用及有效的故障诊断方法，变压器的5 种故障特征气体(H2，C2H4，C3H6，C2H2和CH4)的比值关系与故障类型有着紧密的映射关系，通过这种比值关系［1］就可以有效地探测变压器潜伏性故障而得到国内外的公认［2，3］，它体现变压器内部的潜伏性故障及其发展程度。然而基于三比值法的缺编码和编码边界过于绝对等的不足，近年来，人工智能的方法(专家系统、人工神经网络、聚类分析［4，5］、小波分析等)已经被应用于电力变压器故障预测诊断，并取得了显著的成果。但又由于目前网络存在的训练速度慢、变压器故障不确定性及故障与样本数据之间的非线性特点等，这些都给变压器故障的正确诊断带来障碍。模糊聚类算法在变压器器故障诊断中也有一定的应用，但是传统的模糊聚类受样本分布和初始参数影响大，而微分进化算法是基于种群进化优化的全局优化算法，它在优化问题中都表现出了很好的优化性能，在变压器故障诊断中也得到了应用。但是传统的微分进化算法存在过早收敛，易进入局部极值的缺陷，针对这些问题，利用了自适应调整策略对微分进化进行改进，使用改进后的微分进化对模糊目标函数进行优化，再利用广义神经网络本身所具有的训练速度快，非线性映射能力强等特点，且省去了BP神经网络的权值和阀值的繁琐工作，进而得出故障诊断类型，由实验结果看出，所用算法明显的改善了故障诊断准确度及速度，更有利于对变压器故障进行正确诊断。

2 改进微分进化算法

DE算法是Rainer Storn和Kenneth Price提出的一种实数编码的基于种群进化的全局优化算法，是一种全局搜索能力很强的算法。先对种群进行初始化，然后通过对种群进行变异、交叉和选择等操作，使得种群进化到接近最优解状态［6］。

微分进化算法虽然有很多优点［7］，但在运行中主要受到参数β和CR的影响，这两参数这对种群搜索过程的鲁棒性和收敛速度影响很大。当β较小时，可能算法会出现过早收敛，而β过大时，可能错过局部最优。而CR较小使得新种群个数变少，而CR过大种群却失去稳定性。

为避免传统微分进化算法易出现过早收敛现象，根据遗传算法中交叉和变异思想，本文提出自适应调整策略对传统微分进化算法进行改进，其基本原理是对控制参数β和CR进行自适应调整，即:

式(1)、(2)中，¯β是控制参数的最大和最小值的平均值;¯C是交叉因数的最大和最小值的平均值;λmax和λ分别是最大迭代次数和最小迭代次数，α为经验常数取为3。

3 模糊聚类算法模型

模糊聚类算法的基本思想是要把需要识别的事物与模板进行模糊比较，从而得到所属的类别［8］。模糊聚类算法把n个数据向量xk分成c个模糊类，并求每类的模糊聚类中心［9］，使得聚类目标函数J最小，模糊聚类目标函数为:

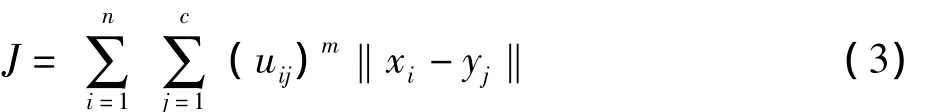
式(3)中uij为个体X属于第j类的模糊隶属度，m为模糊权重指数且m＞1，vj为第j类的聚类中心;通过目标函数J我们可以得出满意的聚类结果;其中uij和vij分别为式(4)、式(5):

当‖xi-vk‖ =0 且k=j时，uij=1;当‖xi-vk‖=0 且k≠j时，uij=0

使用的模糊聚类算法，根据样本的自然状态可以消除样本分布不均匀和存在的孤立点，得到的聚类结果也更趋于合理，通过聚类结果对数据分类，就可以得出训练广义神经网络的训练数据，使网络性能得到提高，也就提高了FCM广义神经网络的精度。FCM聚类算法流程图如图1所示。

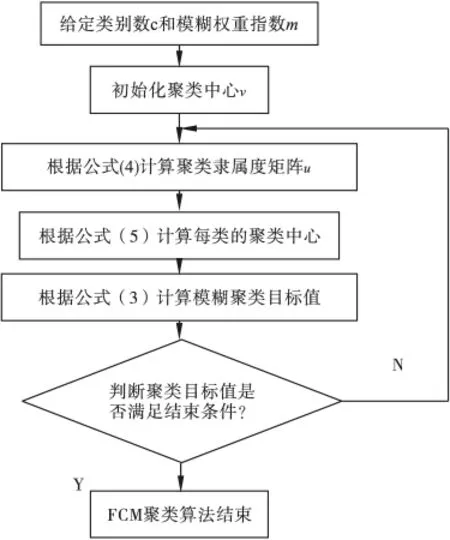
图1 聚类算法迭代过程

通过以上模糊聚类算法可以得到了模糊隶属矩阵u，个体根据隶属度矩阵u每列最低元素位置判断变压器故障样本数据所属故障类型，从而得到最优的模糊聚类，利用模糊聚类结果对故障样本数据进行分类，靠近聚类中心的样本数据作为网络的训练数据并进行模糊聚类结果的统计，为下面训练广义神经网络提供有效训练数据。

4 广义神经网络

所用的广义神经网络分别由输入层、模式层、求和层和输出层构成，与此广义神经网络结构相对应的网络输入、输出分别为X=［x1，x2，…，xn］T，Y=［y1，y2，…，yn］T。广义神经网络具体每层功能结构如下:

4.1 神经网络输入层

文中经过模糊聚类分类的故障样本数据输入向量维数即可作为网络输入层神经元个数，基于输入层神经元是简单的分布单元，可以直接将输入变量传递给模式层。

4.2 神经网络模式层

设故障样本数目为n，则n为模式层神经元数目，模式层的各个神经元对应不同的样本，因此有神经元传递函数pi，如下式:

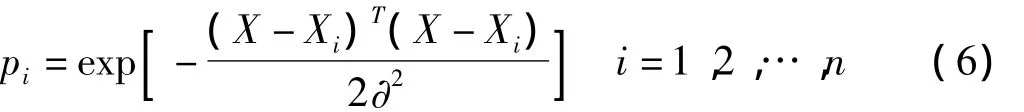
式(6)中，X为网络的输入变量;Xi为第i个神经元相对应的故障样本数据。

4.3 神经网络内求和层

由于模式层与求和层的链接权值的特点，求和层利用了两种不同类型的神经元进行求和。

(1)当模式层神经元与求和层的各个神经元之间的链接权值为1时，求和层的传递函数SD为模式层神经元的线性求和:

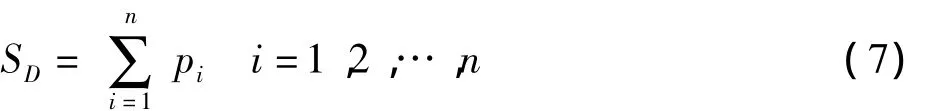
(2)当模式层中第i个神经元与求和层中的第j个分子求和神经元之间的链接权值为第i个输出样本Yi中的第j个元素时，此时的求和层传递函数S为模式层神经元的加权求和:

4.4 神经网络输出层

网络的输出向量维数k为输出层中的神经元数目，神经元j的输出对应估计结果^Y(X)的第j个元素，得输出层神经元yi为:

5 电力变压器故障诊断模型的实现

为了诊断的有效性和实用性，同时根据改良三比值法编码规则及故障类型，选择了变压器的五种故障特征气体作为神经网络的输入变量，以其中的五种典型故障类型(正常状态、局部放电、电弧电、电弧放电兼过热、低能(火花、放电)作为神经网络输出。本文采集了变压器油色谱历史实验记录和相应的历史实验故障类型，并且选择200台变压器作为实验记录，其中的150台作为网络训练样本(正常状态30台，局部放电70台，电弧放电40台，电弧兼过热40台，低能(火花、放电兼过热20台)，剩下50台作为验证样本。

本文网络训练初始数据选择模块根据改进微分进化算法的适应度函数对模糊聚类目标函数J进行优化，进而得到模糊聚类结果，将模糊聚类的结果选择最靠近每类中心的样本做为广义神经网络聚类［11］的训练样本数据，广义神经网络预测模块使用训练好的网络来诊断预测全部输入的故障样本数据X的输出序列Y。本文使用的改进微分进化与模糊聚类广义神经网络对变压器故障诊断预测［12］，本文算法的具体故障诊断流程如下:

第一步:随机选择故障特征量数据作为初始种群，将变压器故障样本数据进行归一化处理，即

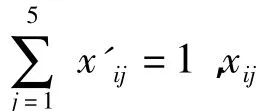
第二步:设置改进的微分进化参数，NP=30，控制参数β在区间(0.5，0.8)变化，交叉因素CR在区间(0.3，0.6)之间变化，最大迭代次数为200，将模糊聚类目标函数J作为改进微分进化算法的适应度函数进行优化，得出最优的聚类结果。

第三步:由所得到的聚类结果数据作为广义神经网络的初始训练数据，并对网络进行训练与预测，得出训练数据，判断所训练网络是否满足要求，若满足要求则进行第四步，否则返回第三步继续训练网络。

第四步:输出网络训练结果，根据结果可以进行故障类型的判断。

6 实验结果分析及验证

6.1 实验结果性能分析

所用算法模型通过MATLAB对流程编程实现［13，14］，得出本文算法的实验预测结果。图2为本文算法与改进DE微分进化广义神经网络及FCM广义神经网络的训练过程的网络逼近结果图，由图2的仿真结果可知，本文算法的网络逼近结果很好，收敛性好，很接近目标预测网络，其网络的逼近误差很小为0.01，而其他两个的网络逼近效果比较差，逼近效果不理想，误差都大于0.1，即改进DE与FCM结合的网络的逼近效果最好，说明预测精度也最高。

从实验结果数据得出改进DE与FCM广义神经网络的变压器故障诊断较改进DE神经网络和FCM神经网络算法在诊断准确率方面确实有了明显提高，而且在本文的算法诊断中，当迭代次数增加时，使得网络的逼近效果更加明显，即网络训练预测更加接近实际值，也就是随着迭代次数的增加，诊断准确率有所提高，但是并不是完全的随着迭代次数增加而增加，实验中当迭代到23次，基本达到本文的最高准确率98.7%，之后随着迭代次数大于23次准确率几乎保持不变约为98.7%，所以从诊断率来看，本文的故障诊断准确率已达90%以上，基本上可以对变压器潜伏性故障进行正确反映。而且本文算法网络的收敛速度很快，即收敛所用时间相比其他两种算法要少很多，诊断结果也是可靠的，利用本文算法能够及时正确的发现故障类型，有利于减少不必要的损失。

图2 网络训练的逼近结果比较图

6.2 实验结果验证

为了验证网络预测的准确度，本文在30台实验样本中随机拿出5台不同的变压器故障类型作为样本实例，将本文算法结果与改进DE广义神经网络结果及FCM广义神经网络算法结果进行比较具体故障类型诊断，由表1可以看出在DE广义神经网络不能诊断出正常状态这一故障类型，FCM广义神经网络不能正确诊断出局部放电状态和低能放电这两种状态类型时，改进的微分进化与模糊聚类广义神经网络却可以正确诊断出，说明本文算法相对其他两种神经网络在精度上确实有所改善。

表1 故障实例与DE广义神经网络及FCM广义神经网络诊断结果比较

7 结论

利用改进微分进化对模糊聚类目标函数进行优化，同时广义神经网络的有导师学习能力完成对变压器故障特征数据的聚类，缩短了收敛到最佳的训练时间，解决了模糊聚类无导师学习能力的不足，提高了训练速度，能够较好的解决实际问题，从而得到比较满意的诊断结果，满足变压器故障诊断的要求，而且模型简单容易实现，具有一定的泛化性。同时基于油纸绝缘引起的变压器故障特量还包括(CO、CO2)，而本文算法却限制这些变量的预测，故要能更加全面的诊断变压器故障类型，还应该继续对变压器的故障特征量与故障类型之间的关系进行更加全面完善的改进。

［1］操敦奎.变压器油色谱分析与故障诊断［M］.北京:中国电力出版社，2010.

［2］徐文，王大忠，周泽群，等.结合遗传算法的的人工神经网络在电力变压器故障诊断中的应用［J］.中国电机工程学报，1997，17(2):109-112.

［3］钱政，罗承沐，严璋，等.范例推理结合神经网络诊断变压器故障［J］.高电压技术，2000，26(4):4-8.

［4］束洪春，孙向飞，司大军.电力变压器故障诊断专家系统知识库建立和维护的粗糙集方法［J］.中国电机工程学报，2002，2(2):31-35.

［5］李俭，孙才新，陈伟根，等.灰色聚类与模糊聚类集成诊断变压器内部故障的方法研究［J］.中国电机工程学报，2003，23(2):112-115.

［6］Storn Rainer.Designing nonstandard filters with differential evolution［J］.IEEE Signal Processing Magazine，2005，41(12):74-75，222.

［7］王敏.分类属性数据聚类算法研究［D］.镇江:苏州大学，2008.

［8］冯琦，周德云.基于微分进化算法的时间最优路径规划.计算机工程与应用，2005，41(12):74-75，222.

［9］马飞.数据挖掘中的聚类算法研究［D］.南京:南京理工大学，2008.

［10］蔡金定，王少芳.基于Roughset理论的改进三比值故障诊断方法［J］.电工电能新技术，2004，23(4):8-12.

［11］刘秀清，宇仁德，范东凯.基于广义神经网络的交通事故预测［J］.山东理工大学学报:2007，21(2):28-31.

［12］谷志红，牛东晓，王会青.广义神经回归神经网络模型在短期电力负荷预测中的应用研究［J］.商场现代化，2008(26):195.