钢－混凝土组合结构中PBL剪力连接件极限承载力比较

林 云，王清远

(四川大学建筑与环境学院，四川成都610065)

钢－混凝土组合结构，是钢部件和混凝土或混凝土部件组合成为整体而共同工作的一种结构，具有钢结构和混凝土结构的一些共同性能。而在组合结构中，钢构件和混凝土构件是利用剪力连接件来共同工作的。所以，在组合结构中，首先要考虑的就是剪力连接件的力学性能。较为常用的剪力连接件是栓钉剪力连接件，但是由于PBL剪力连接件具有比其他传统连接件更好的力学性能，因此PBL剪力连接件的应用越来越广泛。而剪力连接件最关心的就是其极限承载力，下文通过对比国内外不同学者的极限承载力公式，给出几点PBL剪力连接件进一步研究的建议。

1 PBL剪力连接件简介

PBL剪力连接件基本形式是在钢板上开孔后浇注混凝土，利用穿过孔中的混凝土榫来抵抗剪力流;或者在孔中穿过钢筋。这种结构最先是由德国E·F·Leonhardt(1987年)教授开发出来的。后经各国学者不断地研究和创新，又产生了很多不一样的PBL剪力连接件。比如，Twin－PBL剪力连接件和S－PBL+栓钉剪力连接件等。

2 国外主要PBL剪力连接件计算公式

1987年，Leonhardt等人最先提出PBL剪力连接件的概念，他们基于设有贯通钢筋试件的试验结果，认为PBL剪力连接件的主要破坏形式是混凝土榫的剪切破坏，所以在他们提出的计算公式中并不直接反应贯通钢筋的影响，并提出如下的计算公式:

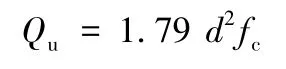
Oguejiofor和Hosain利用梁上375mm长的剪力键进行试验，得出剪力键破坏是因为混凝土板沿着连接线劈裂所致。PBL剪力键的承载力是由钢板外混凝土、横向普通钢筋和混凝土榫共同控制。他们考虑了很多的物理因素，并给出了以下计算公式:

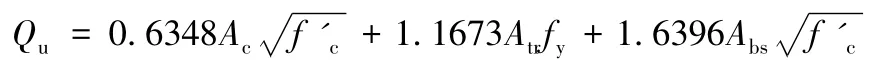
式中:Ac是连接器平面中混凝土的面积;Atr是横向普通钢筋的面积;Abs是混凝土榫的受剪面积。

Oguejiofor和Hosain(1996)随后又进行了试验，并对结果进行回归分析，提出了一个新的公式，这个公式与之前他们提出的公式差别不大，只是改变了相关系数。

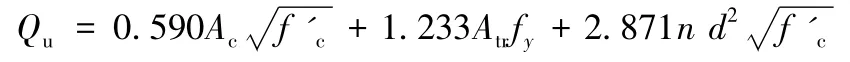
式中:Ac是混凝土的剪切面积;Atr是通过孔洞的横向钢筋的面积。

Nishiumi等人(1999)则把贯通钢筋的影响看成是侧面的约束力，根据试验中的贯通钢筋的应变大小，观察到达到最大承载力时钢筋都已屈服这一现象，为此把钢筋屈服时的作用力看成是最大承载力时的约束力。并根据试验数据建立了抗剪强度与侧面约束强度的回归曲线，得出了下面的公式。

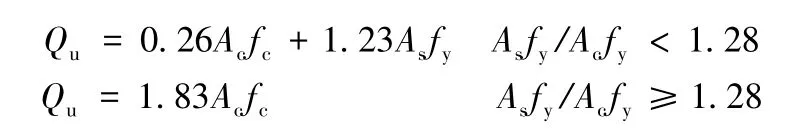
式中:Ac是圆孔的面积;As是贯通钢筋的面积。

Hosaka等人(2002)认为贯通钢筋的影响较大，应该加以考虑，所以PBL剪力键的承载力由混凝土榫和孔洞中的贯通钢筋共同控制，并将试验数据进行回归分析提出了如下的计算公式。

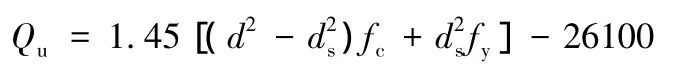
后来，Oguejiofor和Hosain又进行了更多的试验并给出了一个新的计算公式，这个公式能够更好的量化剪力键的抗剪能力，并且在公式的第一部分考虑了剪力键的端部承压强度。

式中:h和t分别为PBL键钢板高度和厚度;Atr是通过孔洞的横向钢筋的面积。

欧洲规范4(Ecrocade4)(2007)通过对各国大量的试验资料进行统计分析，取平均值减去2倍标准差的下限作为PBL剪力键的极限承载力，给出了以下的计算公式。

(1)无贯通钢筋时

以上公式中，Qu是极限承载力;fc是混凝土的立方体抗压强度;f'c是混凝土圆柱体抗压强度;ft是混凝土的轴心抗拉强度设计值;d是孔洞直径;ds是横向贯通钢筋的直径;n是孔洞个数。

3 国内主要PBL剪力连接件计算公式

福州大学的宗周红等人(1999)共进行了9只栓钉连接件和6只带孔钢板连接件的疲劳和静载破坏试验研究，并利用试验结果分析各参数对承载力的影响，首次考虑了混凝土类型的影响，并建立了如下的计算公式。

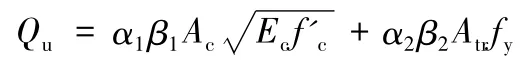
式中:α1为混凝土类型的影响系数，普通混凝土取1.0，钢纤维混凝土取1.25;α2为横向钢筋的位置影响系数，通常情况下取1.0，当与受剪相反方向的横向钢筋较多时取1.5;β1、β2为回归系数;分别取0.0029和0.75;Ac为混凝土纵向面积减去钢板面积;Atr、fy为横向钢筋的总面积和屈服强度。此公式还能应用于计算栓钉的极限承载力，具体见文献[6］。

湖南大学的胡建华等人(2006)设计制作了15组不同的PBL试件共44个，完成了极限承载力试验，并指出连接件的破坏模式是剪切破坏，其抗剪承载力由钢筋(包括贯通钢筋和横向普通钢筋)和混凝土榫两部分共同提供，明确区分了横向普通钢筋和贯通钢筋的作用，并推导出如下计算公式。

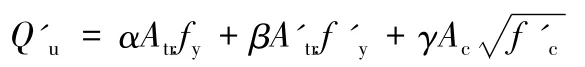
式中:Q'u为单孔极限承载力;Atr、A'tr分别为贯通钢筋和横向普通钢筋的面积;fy、f'y分别是贯通钢筋和横向普通钢筋的屈服强度;Ac为混凝土榫的面积;α为钢筋影响系数，取1.320125;β为横向普通钢筋的影响系数，当配箍率ρ≤0.18%时，取 1.204479，当 配 箍 率 ρ＞0.18%时，取1.042948;γ为混凝土榫影响系数，取1.95168。

西南交通大学的张清华等人(2007)为了使剪力键的计算公式物理意义更加明确，通过大量的试验数据并进行回归分析提出了如下PBL剪力键极限承载力计算公式。

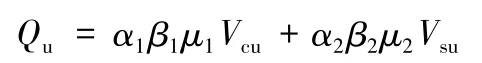
剪力键中贯通钢筋延性破坏时，

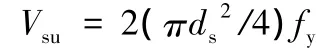
剪力键中贯通钢筋脆性破坏时，

式中:Vcu和Vsu分别为剪力键中混凝土榫和钢构件部分所承担的承载力;α1和α2分别为混凝土类型的影响系数和横向钢筋影响系数，通常情况下都取1.0;β1和β2均为回归系数;μ1和μ2分别为混凝土榫和贯通钢筋的破坏类型系数，延性破坏时，μ1=μ1=1.0，脆性破坏时，μ1=1.6，μ2=1.2;fu为钢筋的极限强度。此公式还能应用于计算多个剪切面以及栓钉的极限承载力，具体见文献[9］。

4 结束语

综上所述，有以下几点建议供今后进一步进行PBL剪力连接件试验研究参考。

(1)国内外到目前为止没有形成完整的规范来指导PBL剪力连接件的试验，并且由于各个研究人员采用的试验形式不尽相同，导致了各自的计算公式也不相同。为了使PBL剪力键更加广泛地应用于组合结构中，应该尽快规范PBL剪力键试验的试件规格和试验方法。

(2)国内外目前大部分研究人员都是利用试验数据进行回归分析后得出与自己的试验结构基本一致的计算公式;而只有少部分研究人员采用ANSYS等有限元软件进行模拟。所以有关PBL剪力连接件的有限元分析是值得深入研究的方面。

(3)PBL连接件的静载试验研究较多，而有关疲劳性能的研究较少。以后应加大其疲劳性能的研究。

[1]聂建国，刘明，叶列平．钢－混凝土组合结构[M］．北京:中国建筑工业出版社，2005

[2]Leonhardt E F，Andrae W，Andrae H P，et al．Neues vorteilhaftes verbundmittel fur stahlverbundtragwerke mihoher Dauerfestirkeit[J］．Beton und Stahlbetonbau1987，82(12):325－331(in German)

[3]刘玉擎，曾明根，陈艾荣．连接件在桥梁结构中的应用与研究[J］．哈尔滨工业大学学报，2003，35(8):272－275

[4]Oguejiofor E C，Hosain M U．Numerical analysis of push－out specimens with perfobond rib connectors[J］．Computer＆Structures，1996，62(4):617－624

[5]Valente I，Paulo J S．Cruz．Experimental analysis of Perfobond shear connection between steel and lightweight concrete[J］．Journal of Constructional Steel Research，2004，60:465－479

[6]Eurocade4，Design of Composite Steel and Concrete Structures[S］．BSI，London，1994

[7]宗周红，车惠民．剪力连接件静载和疲劳试验研究[J］．福州大学学报(自然科学版)，1999，27(6):61－66

[8]胡建华，叶梅新，黄琼．PBL剪力连接件承载力试验[J］．中国公路学报，2006，19(6):65－72

[9]张清华，李乔，唐亮．桥塔钢－混凝土结合段剪力键破坏机理及极限承载力[J］．中国公路学报，2007，20(1):85－90