水平常幅荷载作用下塑性铰滞回衰变特征对RC框架结构屈服力的影响

王飞娅，张 伟，余立军

(1．广州城建职业学院建筑工程管理系，广东广州510925;2．湖南百利工程科技有限公司，湖南益阳414000;3．安徽省交通勘察设计院广州分院，广东广州510620)

在地震发生的过程中结构经历显著的弹塑性变形。在结构性能没有损伤之前，结构的强度、刚度和稳定性受最大响应位移控制。在结构开始损伤后，反复的非弹性位移循环会导致结构的强度和刚度降低，也就是结构的性能降低[1］。由于将框架结构塑性发展区域集中在塑性铰部位，因此各塑性铰性能的退化决定了结构抗侧刚度的退化，进而决定了结构构件的屈服力的退化。

1 基于能量的恢复力模型

利用17根钢筋混凝土梁进行了17组不同的实验[2］。该试验还通过归一化处理试验数据后，得到一条在常幅荷载作用下的名义耗散周期曲线，并用一个能代表这条平均曲线的指数函数来分析构件能量耗散的形式，如图1。

图1 含γ，β两个参数的耗能示意

这条平均曲线所代表的指数函数为:

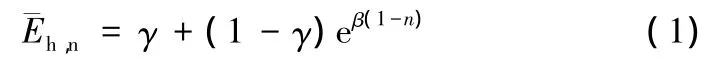
公式中:珔Eh，n是在周期为n的名义耗能;1－γ是能耗能力;β代表损伤速度。

当n=1时:

表示在第一个周期内的名义能耗恒为1.0。

当n→∞时:

表示构件不会在随荷载的低周往复作用而耗散能量。

珔Eh，n的函数式包括n，γ，β三个参数。由图1可以看出随着循环次数n的增加，珔Eh，n的值都是随循环周期数n的增加而减小的。图1对γ，β的限制情况进行了说明。γ=0表示耗散所有的能量，当n趋于无穷大时，γ=1表示不耗散任何能量。因此，γ=0表示一个在刚度和强度中的严重的耗散系统，γ=1表示理想弹塑性非耗散的滞回系统。第二个参数β在0和无穷大之间变化，它表示在周期能耗能力的速率。在极限情况下，β=0是一个没有耗散的理想系统，它表示在完成第一个周期后损失所有的能量。珔Eh，n的值在(γ，1)这个区间范围内，当n无穷大时珔Eh，n的值不在减小为γ，β的取值，影响珔Eh，n的值从1衰减到γ的速度快慢。由图1可以看出当β=0时珔Eh，n的值在n=1(即第一个周期)时就耗散了所有的能量。β=∞时珔Eh，n的值衰减的速度最慢，其衰减路径ABC。图1中曲线AC为β取(0，∞)之间的值时的衰减路线，近似为指数曲线。则γ决定珔Eh，n的衰减值和衰减剩余值，β决定珔Eh，n的衰减速度。最终珔Eh，n的值随着循环次数n的增大而减小。

2 恢复力模型的定量描述

该实验还确定了一个强度退化的双线型恢复力模型。模型为一个强度退化的双线型恢复力模型，并可预测等幅荷载位移循环下的能源耗散。其滞回环包围面积表示在一个循环下，该构件的滞回耗能量(图2)。

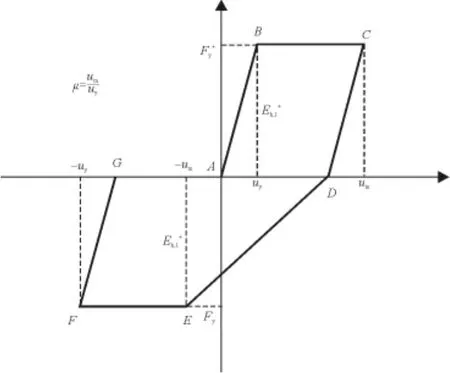
图2 试验中提出的基于能量的低周疲劳模型

图2表示当n=1时，钢筋混凝土构件的第一个滞回环。由图2中的几何关系可以看出:

式中:Fy为构件的屈服力;um为构件的最大弹塑性位移;uy为构件的屈服位移;Eh，1为构件经历第一次荷载循环后的滞回耗能量。

假定位移最大值um保持不变，则每次使构件达到相同最大位移的能量随着荷载循环次数n的增大而减小。因为在滞回曲线中滞回环的面积代表了构件耗散的能量，则在荷载循环加载一次到达um的值后，滞回环所包围的面积也减少。由基于能量提出的这个滞回曲线的特性可以定性地描述该构件经历常幅荷载加载n个循环周期的滞回曲线。即恢复力模型，见图3。

图3 理想的双线型非弹性体系恢复力模型

以3个循环周期为例，从图3可以看出:

当循环周期n=1时，周期路径为ABCDEFG;n=2时，周期路径为GHJKL;n=3时，周期路径为LMNOP。

在恢复力模型中每一个循环中作用力和位移与循环周期的对应关系见表1。

表1 恢复力模型中每一个循环中作用力和位移与循环周期的对应关系

从图3中的几何关系可以看出:

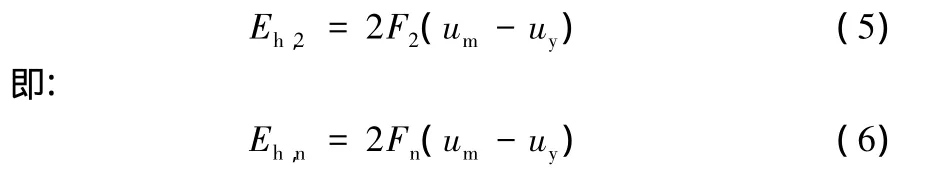
又由比例关系有:

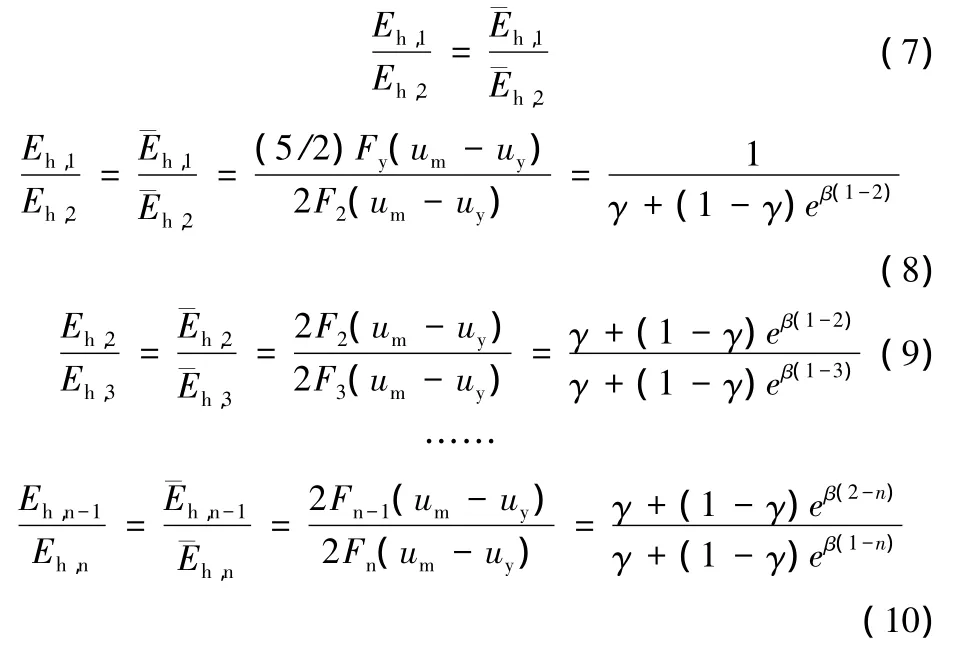
联立式(8)，式(9)，式(10)则可推出:

由上式可求出图4中对应的F2，F3，F4，…，Fn的值。在定性描述的基础上定量的描述了此恢复力模型。确定了塑性铰滞回衰变特征对RC框架结构构件屈服力的影响。

3 总结

一般而言，对结构施加外力，结构会有相应的反力产生。如果结构产生的反力足以抵抗外力对结构的作用则结构处于弹性变形。如果外力作用超过了结构的承载能力结构就会被破坏，结构处于弹塑性变形。

钢筋混凝土结构累积损伤破坏的特点是结构位移没有超过某一限值，但位移往复次数的增加仍导致结构破坏，这表明随着损伤的加剧，结构发生倒塌的位移限值是一个不断变小的量。结构的倒塌源于二阶效应不稳定，而该稳定性可以通过结构刚重比进行控制，所以结构位移限值的变化取决于刚重比值的变化，即结构抗侧刚度的变化。由于将框架结构塑性发展区域集中在塑性铰部位，因此各塑性铰性能的退化决定了结构抗侧刚度的退化，进而决定了结构构件的屈服力的退化。

[1]刘哲锋，沈蒲生，胡习兵．地震总输入能量与瞬时输入能量谱的研究[J］．地震工程与工程振动，2006，26(6):31－36

[2]Altug Erberik，Haluk Sucuoglu．Seismic energy dissipation in deterioratingsystemsthroughlow－cyclefatigue[J］．Earthquake Engineering and Structural Dynamics，2004，33:49－67