六自由度并联微动机器人全闭环控制系统研究

丰 茂

（国家知识产权局专利局专利审查协作北京中心，北京100190）

微动并联机器人因具有运动精度和分辨率高、自身体积小、刚度大等特点，目前已在MEMS制造、光学调整、激光制导、生物医疗、IC制造等微操作领域得到了广泛的应用［1－4]．但是由于制造及装配等误差因素，使得并联微动机器人的精确定位不易实现．针对提高定位精度的方法，已进行了很多相关的研究．吴江宁等［5]通过经纬仪测量运动平台的系列变化位姿，间接计算六自由度平台的实际结构参数并在控制软件中进行补偿以提高位姿精度．陆敏智等［6]研究了6－THHT型并联机器人基于多传感器数据融合技术的反馈测控系统，探讨了并联机器人六路驱动杆的闭环反馈控制的实现方法，为直接对动平台实现全闭环控制提供了理论依据．Rainer Tutsch等［7]利用集成于并联机器人的3D传感器，设计配置了基于多通路线阵CCD图像采集设备的测量系统，使得机器人的定位精度达到1μm．

为了提高精度，本文提出一种基于集成传感器的新型三杆六自由度并联微动机器人的末端位姿检测及全闭环控制的方法．

1 结构组成

图1为3－PPSR并联微动机器人的结构示意图．三根固定长度的连杆3连接动平台1和底座9，支杆上端采用单轴柔性铰链2作为输出，下端采用柔性球铰链5作为输入，支杆上端三个铰链中心点和下端三个铰链中心点均呈等边三角形分布．下平台包含整体加工的三个二维微动平台4，采用了结构简洁的直角双层弹性平板结构．测量末端位姿所需的测量辅助装置6与动平台固连，7与底座固连．测量所用的传感器8安装在7上．

并联机构的上下平台坐标中心到柔性铰链中心点的距离分别为10mm、50mm，杆长为60mm．

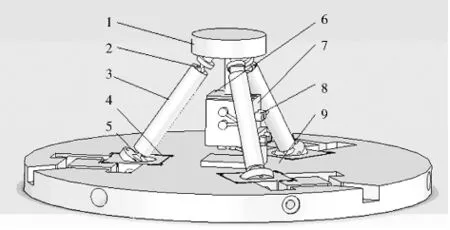
图1 3－PPSR并联微动机器人结构示意图

每条支链均采用双输入结构，即由2个压电陶瓷驱动双输入弹性平板来实现X和Y两方向的输入，驱动采用PZ公司的PSt150／7／7vs12型压电陶瓷．3条支链输入端总计3组双弹性平板、6个压电陶瓷均集成在基座上，由于每条支链输入为2个自由度，因而在3个支链末端可实现六自由度微运动．

设下端3个球铰中心点分别为Bi（i＝1，2，3），建立如图2所示坐标系B－XYZ，原点为B（三角形中心）．同理，设上端3个单轴柔性铰链中心点分别为Pi（i＝1，2，3），动坐标系原点P建在Pi中心，PX＇Y＇Z＇的X＇轴与B－XYZ的X轴平行，P－X＇Y＇Z＇的Z＇轴与B－XYZ的Z轴重合．

设b为B到Bi长度，同理，p为P到Pi长度．零位时Bi点坐标为［b·cosλi，b·sinλi，0] ，零位时Pi点在动坐标系中坐标为［p·cosλi，p·sinλi，0] ．其中i＝1，2，3；λi＝（i－1）×120°．△Mi和△Ni分别为压电陶瓷的输出位移，其中i＝1，2，3，且i＝1时，i＋1，i＋2分别代表2，3；i＝2时，i＋1，i＋2分别代表3，1；i＝3时，i＋1，i＋2分别代表1，2．动坐标系沿固定坐标系X轴微小平移△x，沿Y轴微小平移△y，沿Z轴微小平移△z，绕X轴旋转微小角位移△α，绕Y轴旋转微小角位移△β，绕Z轴旋转微小角位移△γ，通过几何关系对微动并联机器人进行逆

图2 并联微动机器人参考坐标系

解可得

写成矩阵的形式，可以得到微动并联机器人的位置逆解方程：

式中：J为常数矩阵，所以其正解方程为

预紧力对压电陶瓷的最终输出有着较大的影响，在空载时压电陶瓷在施加最大电压（150V）时最大输出为9μm，预紧后仅为7μm，所以在进行工作空间仿真时，取压电陶瓷的实际最大行程为7μm．图3所示为运用Matlab数学计算软件对微动机器人的工作空间进行仿真的效果图．

图3 微动机器人工作空间仿真效果图

通过对工作空间的仿真，可以得到3－PPSR微纳米操作机器人在单个X或Y向上的行程大约为±4μm，在Z向上的行程为5μm．

2 测量方法

为了实现并联微动机构的末端位姿全闭环控制，增加了传感器测量装置，并将其与并联机器人集成，构建由压电陶瓷器件、压电陶瓷驱动电源、微位移传感器、微定位控制器和微动机构组成的位置全闭环控制系统，以实现机构、驱动、末端检测反馈一体化．

为了能够同时测量6个自由度，那么需要6路测量装置，本文测量所需的传感器采用MTI公司的ASP－1－ILR探头式电容传感器．将6个电容传感器以图4所示的方式分布在相互垂直的3个平面上，并用紧钉螺钉固定在探头连接装置上．为了便于计算，在安装传感器时，应使传感器所在坐标系与微动并联机器人的动平台所在坐标系平行．由于被测量装置与动平台是紧固连接的，所以传感器测被测装置实际上就是用传感器直接测量上平台．下面以一个面上的两个传感器为例，介绍测量的步骤和方法．

图4 集成了传感器的测量装置示意图

如图5所示，S1，S2分别为初始状态时两个传感器所对应的投影在被测装置的位置，为了便于计算，将S1，S2对称分布于坐标系原点两侧，两者之间的距离为固定值D，且平行于y轴，测量方向沿x轴向．S′1，S′2为动平台运动后在被测装置上传感器投影的位置，那么ΔXS1，ΔXS2分别为被测装置即动平台在固定的传感器探头所在直线方向上的位移，该值可由传感器直接读出．

图5 测量几何关系图

3 闭环控制及误差补偿

3．1 误差补偿模型

通过传感器测得的位姿与期望位姿的比较，建立如图6所示的微动并联机器人的位姿误差补偿模型．

图6 微动并联机器人位姿误差补偿原理图

设X（p）为机器人的期望位姿，通过逆变换，可得出机器人末端到达X（p）时的压电陶瓷的输出位移M，所对应的驱动电压为U．但由于机器人机构存在各种误差Δp，这样当各压电陶瓷输出位移为M时，末端传感器测得的机器人末端的实际位姿为X（p＋Δp），通过逆变换，可以得到末端的实际位姿为X（p＋Δp）时的压电陶瓷的输出位移为MΔM，所以得到误差e＝ΔM．

为了校正机器人末端的位姿，用一个预置的位姿偏移量－Δp，使机器人末端的指令位姿预置为X（p－Δp），即对各输入电压进行修正，使得压电陶瓷驱动电压为U＋ΔU，补偿各压电陶瓷一定的输出位移ΔM，此时对应的压电陶瓷的输出位移为M＋ΔM，预置的位姿偏移量－Δp与机器人机构误差Δp相互抵消，即得到机器人的期望位姿X（p）．在这个过程中，需要循环多次的进行误差补偿，以达到所需要的定位精度．

3．2 控制方法研究

传统的PID控制器是利用一组固定的参数进行控制，不能兼顾动态和静态、设定值和抑制扰动之间的矛盾．因此，我们引入模糊推理，在初值基础上适当调整PID的参数，从而改善系统的控制效果．利用模糊控制规则在线对PID参数进行修改，便构成了模糊PID控制器［8]，模糊PID控制器是以偏差e和偏差变化率ec作为输入，利用模糊规则对比例、积分和微分参数进行在线调节．e（nT）和ec（nT）定义如下：

式中：T为为采样时间；r（nT）为给定的理论值；y（nT）为第n个采样时刻实际值．

在进行闭环PID控制时，积分参数KI会增加系统响应的快速性，消除静差，但其值过大会引起系统的超调，甚至不稳定；比例参数KP过大容易引起系统振荡，反而使调节时间加长，且当KP太大时，系统将趋于不稳定状态；微分参数KD对系统性能的影响很小，因此一般KD的取值可以忽略．为简化控制设计，将数字PID控制器简化为数字PI控制器，忽略微分项的作用，其结构如图7所示．

图7 模糊PI控制原理图

模糊控制器以误差e和误差变化ec作为输入，PID参数模糊自整定是找出PID中3个参数与e和ec之间的模糊关系，在运行中通过不断检测e和ec，根据模糊控制原理来对3个参数进行在线修改，以满足不同e和ec时对控制参数的不同要求，而使被控对象有良好的动、静稳态性能．

3．3 控制系统的设计

在对3－PPSR微动并联机器人的各结构参数进行辨识的基础上，用辨识结果修正系统运动学模型来实现机器人末端位姿的补偿，其具体过程如图8所示，主要分为以下几个步骤：

（1）取一期望的末端位姿rd，根据理想的运动学逆解方程计算此时的压电陶瓷位移．

（2）将压电陶瓷定位到上述位置，测量出此时的末端位姿ra，并与期望位姿比较，得出末端位姿误差δr．

（3）如果末端位姿误差满足要求，则结束；否则进入下一步骤．

（4）依据微动并联机器人运动学逆解公式的特点，可以得到产生末端位姿误差所需的压电陶瓷的输出位移．

（5）通过模糊PID算法，得到对应的压电陶瓷所需位移．

（6）重复步骤（2）～（5），直至动平台实际末端位姿能够足够地接近理想值，从而达到闭环控制的目的．

图8 微动并联机器人闭环控制流程图

4 闭环控制实验

表1为微动机器人在开环、标定和全闭环控制后的定位精度对比，表2为微动机器人在开环和全闭环控制后的重复定位精度对比．

表1 定位精度对比

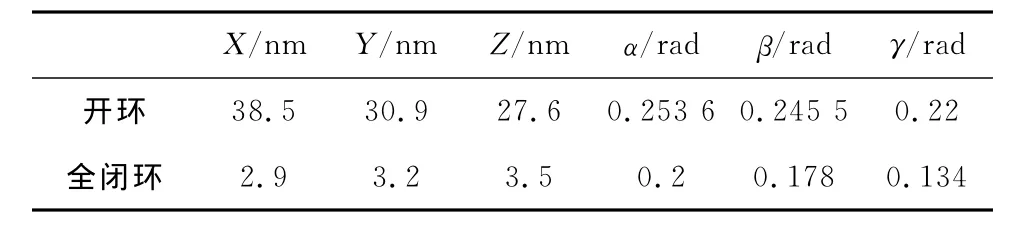
表2 重复定位精度对比

由表1和2可知，全闭环控制后，3－PPSR微动并联机器人的定位精度和重复定位精度均得到了很大提高，并且基本达到期望的末端位姿，从而实现了微动并联机器人末端位姿准确定位．

5 结束语

本文研制出了机构、驱动、位姿检测和闭环控制一体化的3－PPSR高精度微动并联机器人．主要研究工作和结论如下：

（1）采用电容式微位移传感器，提出针对3－PPSR微动并联机器人的非接触式六点测量方法对位姿进行检测．分析了该方法的安装和测量误差，通过对传感器安装位置的比较，获得了最佳的传感器安装方案．

（2）利用高精度电容测微仪得到的末端位姿作为反馈信号，采用模糊PID控制算法，实现了对3－PPSR微动并联机器人的全闭环控制．实验结果表明，执行全闭环控制后，微动机器人的定位精度和重复定位精度均满足性能指标要求．

［1] 矫杰．3－PPSR微动并联机器人的研究［D] ．哈尔滨：哈尔滨工业大学，2006．

［2] 贾庆轩，魏秋霜，孙汉旭，等．并联微动机器人的研究现状［J] ．山东理工大学学报：自然科学版，2003，17（6）：98－102．

［3] Kallio P，Lind M，Zhou Q，et al．A 3DOF piezohydraulic parallel micromanipulator［C] ／／Katholieke U L．International Conference on Robotics and Automation．Leuven：IEEE Robotics and Automation Society，1998：1 823－1 828．

［4] Zhang W J，Zou J，Watson L G，et al．The constant－jacobian method for kinematics of a three－DOF planar micro－motion stage［J] ．Journal of Robotic Systems，2002，19（2）：63－72．

［5] 吴江宁，左爱秋，李世伦．并联六自由度平台机构机械误差分析与检测［J] ．中国机械工程，1999，10（6）：614－617．

［6] 陆敏智．6－THHT并联机器人的多传感器测控系统研究［D] ．南京：南京理工大学，2006．

［7] Rainer T，Marcus P，Michael B，et al．3D－sensor for the control of a micro assembly robot［C] ／／George K K．Optomechatronics Systems IV．San Diego：Society of Photographic Instrumentation Engineers，2003：266－273．

［8] 储岳中，陶永华．基于MATLAB的自适应模糊PID控制系统计算机仿真［J] ．安徽工业大学学报，2004，21（1）：49－52．