四点接触球转盘轴承沟道形状与游隙关系特性分析
2012-07-20陈龙姜红卫王黎峰邱明夏新涛
陈龙,姜红卫,王黎峰,邱明,夏新涛
(1.河南科技大学 机电工程学院,河南 洛阳 471003;2.包钢集团 无缝钢管厂,内蒙古 包头 014000;3.洛阳瑞成轴承有限责任公司, 河南 洛阳 471003)
四点接触球转盘轴承结构紧凑,重量轻,可以同时承受轴向力、径向力及倾覆力矩,因而广泛应用于回转式焊接操作机、中小型起重机和挖掘机等工程设备[1]。四点接触球转盘轴承的沟道为2条圆弧,沟曲率系数为0.52~0.55。一般工程机械设备中,由于游隙大于零,钢球和沟道之间为两点接触;在一些回转精度要求较高或者有启动力矩要求的应用场合(如雷达回转台、机床回转台以及风力发电机变桨装置等),要求转盘轴承采用零游隙或者负游隙,钢球与沟道间为四点接触[2-4]。转盘轴承套圈材料一般选用50Mn钢或42CrMo钢,套圈沟道采用表面淬火;钢球采用GCr15钢或GCr15SiMn钢,整体淬火[5]。依据工况不同,做高频往复摆动的四点接触球转盘轴承常见的失效形式为承载区的疲劳破坏;低频摆动与低速回转常见的失效形式主要为压痕[6]。
由于四点接触球转盘轴承的广泛应用及其在承载上的突出优势,很多学者对于其承载能力做了深入研究。文献[7-10]分析了转盘轴承载荷分布的解析求解方法;文献[11]研究了转盘轴承载荷分布的数值求解方法;文献[12-13]从不同角度分析了四点接触球轴承载荷分布方程的建立方法;文献[14]还建立了确定型号的四点接触球转盘轴承的有限元分析模型,并采用有限元分析方法建立了一些固定型号的柔度矩阵;文献[15-16]提出了四点接触球转盘的数字化设计方法;文献[17]提出了四点接触球转盘轴承的自适应设计方法;文献[18-19]通过试验验证了相关理论分析的正确性。
转盘轴承的安装往往采用螺栓连接[20],因而也有众多学者围绕转盘轴承的螺纹连接特性展开专门的深入研究[21-22]。一些特殊工况(如风力发电机变桨装置)对四点接触球转盘轴承的启动力矩提出了具体要求[23-25],以避免蠕动磨损[26]。为了满足启动力矩要求,使轴承的游隙值小于零从而使轴承装配完成后即预紧。对于直径尺寸较大的转盘轴承,负游隙预紧使得转盘轴承内、外圈发生弹性变形[3],影响内部载荷分布状态[27]。
以上分析均基于各零件的理想几何形状开展,而实际加工过程中的加工误差对四点接触球转盘轴承钢球与沟道的接触位置有着显著影响。接触位置的改变直接影响接触角的大小,进而影响到转盘轴承的游隙值及内部的载荷分布状态。对于负游隙的转盘轴承,游隙值的大小还将进一步影响到轴承启动力矩值。影响四点接触球转盘轴承启动力矩的加工误差主要包括套圈的圆度、沟道接触点位置与基准端面之间的平行差以及沟道形状,其中圆度和接触点位置与基准端面之间的平行差会造成转盘轴承回转过程中出现卡死点,因而在制造过程中得到了足够的重视和严格控制。负游隙靠配制尺寸链内各零件尺寸获取,无法直接测量。由于负游隙的数量级相对较小并且对于启动力矩的影响显著,因而沟道形状对于负游隙转盘轴承的影响也极为突出。
在此,着重分析沟道形状对负游隙转盘轴承游隙的影响,并设计了相关试验验证理论分析的正确性。由于负游隙无法直接测量,试验中采用启动力矩作为间接评判指标来判断负游隙的量。
1 沟道形状及其对游隙影响的理论分析
目前常见的四点接触球轴承沟道终加工方法有两种:一种是表面淬火后采用磨床切入磨加工沟道;另一种是表面淬火后采用数控车床经硬车形成沟道。这两种工艺方法各有优劣。采用切入磨法加工时沟道形状靠砂轮修整出来的形状保证,砂轮修整精度以及磨削过程中的砂轮磨损对于沟道形状有直接影响,难以保证精度要求,但加工特大型的四点接触球转盘轴承往往采用落地磨床,设备投资相对较小并且能得到较好的表面质量;采用硬车方法加工沟道时,由于沟道形状依靠程序保证,因而加工出的沟道形状较好,但加工出的表面粗糙度与磨削相比还有一定差距。
沟道形状对于四点接触球转盘轴承装配完成后的接触角有着直接的影响,而接触角的改变将直接影响转盘轴承的承载能力。一般转盘轴承在承载能力计算及选型计算中,均存在一定裕量,因而对于一般工程机械用转盘轴承来说,因沟道形状造成的接触角变化对轴承应用的影响并不突出。但对于有回转精度和启动力矩要求的负游隙四点接触球转盘轴承来说,沟道形状对负游隙的影响程度大,进而会造成启动力矩变化。
1.1 沟道一致性对游隙的影响
一般设计标准取外圈沟曲率系数fe=0.54,内圈沟曲率系数fi=0.525,但各转盘轴承制造厂此参数选择不尽相同。为了便于以下分析,内、外沟曲率系数均取0.55。图1为零游隙时四点接触球转盘轴承的钢球与4条沟道的接触状态。钢球与内、外圈4条沟道的4点接触,接触角为α0=45°,对角相对的两条沟道的圆弧中心(Oe1,Oi2与Oe2,Oil)位于接触点连线上,中心距Oe1Oi2和Oe2Oi1相等。

图1 四点接触球转盘轴承的接触形式
实际加工中,沟道形状精度难以保证。尤其是采用砂轮切入磨削时,砂轮修整精度不足,或磨削过程中砂轮的磨耗相对较小,以较大的张角终磨形成沟道,则当沟径尺寸加工到规定尺寸后,装配后实际接触位置低于设计值,接触角由原接触角α0变化为α1,接触角减小,钢球与沟道之间由4点接触变为2点接触,如图2a所示,合套完成的轴承游隙由零游隙变化为正游隙;反之,若磨削过程中砂轮自身磨耗过大,则终磨形成的沟道张角小,沟径尺寸加工至规定尺寸后,接触角增大,合套完成的轴承由无预紧的零游隙4点接触变为带预紧的负游隙4点接触,如图2b所示。
以上讨论的仍为理想的加工结果,即内圈或外圈同时出现“大张角”或“小张角”的情形,两条沟道形状一致。但在实际加工中,由于内、外圈沟道分开磨削,需要多次装夹,多次定位,因而两个套圈沟道形状的一致性难以保证,造成理论游隙与实际游隙的差异较为突出。实际中最为常见的状态也是内、外圈2条沟道各自对称性较好,但内、外圈的沟道一致性较差。生产中通常采用弦长偏差控制该指标,虽然一般标准对于弦长偏差的控制较为严格,但由于游隙值本身数量级相对于轴承尺寸非常小,因而目前所控制的弦长偏差对于游隙的影响仍然非常突出。
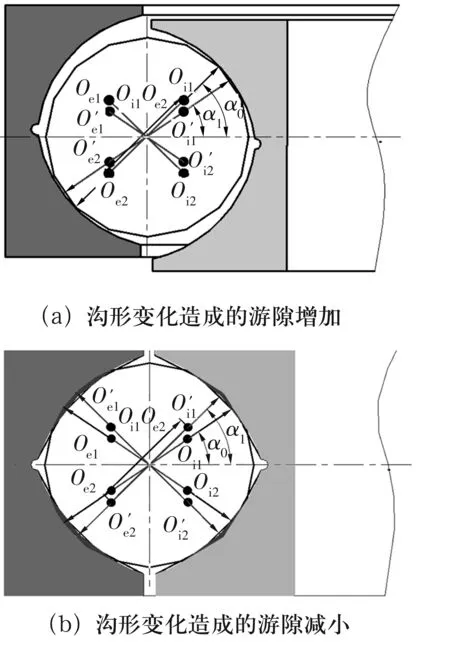
图2 四点接触球转盘轴承的接触
1.2 沟道形状对游隙的影响
为了更清晰地说明沟道形状对游隙的影响规律,以四点接触球转盘轴承球组节圆中心为主坐标系中心,构建如图3所示三维坐标系Oxyz,图中,Dpw为球组节圆直径;α1和α2分别为钢球与外圈上、下沟道的接触角;ϑ为轴承中钢球的位置角;γ为确定位置角处的钢球受径向力在水平xy坐标系的方位角;Oed和Oeu分别为钢球和外圈上、下沟道的接触点。 外圈沟道上某点坐标可以描述为

图3 四点接触球转盘轴承的接触
(1)
式中:R为沟曲率半径。
当轴承沟道形状与理想形状不一致时,钢球的理想位置与实际位置间亦存在差异,则建立钢球实际位置坐标系uvw如图3b所示[14]。若外圈固定,则回转面xOy上的钢球以及内圈存在运转趋势,假定转动角度为φx和φy。根据坐标变换,由于沟道形状变化造成的相对运转趋势可得沟道实际表面距离主坐标原点的表达式
(2)
沟道形状误差一般不会太大,动、静坐标系之间的差异也较小,即φx和φy趋近于0,则cosφx和cosφy趋近于1,sinφx和sinφy趋近于0,则 (2) 式可进一步简化为
。(3)
沟曲率中心距主坐标原点的距离为
(4)
游隙变化量为

(5)
2 试验研究
实际加工中,四点接触球轴承的游隙配制方案为:测量轴承内、外圈直径,测量内、外圈沟道夹球壁厚,测量实际装入钢球直径值,依据内、外沟道的夹球壁厚,内、外圈与钢球总厚度H以及钢球直径计算游隙
Gr=Ki+Ke-H-Dw,
(6)
式中:Ki和Ke分别为内、外沟道的夹球壁厚;H为内、外圈以及钢球的总厚度;Dw为钢球直径。测量原理如图4所示[28],这种测量方法虽然考虑了沟道形状对游隙的影响,但由于测量时以内径面和外径面作为测量基准,而转盘轴承的内、外径精度要求不高,使得测量精度难以保证,尤其当转盘轴承带外齿或内齿时,测量精度更差。另外,测量过程中钢球的固定有一定难度,测量的最大值点也难以找准。
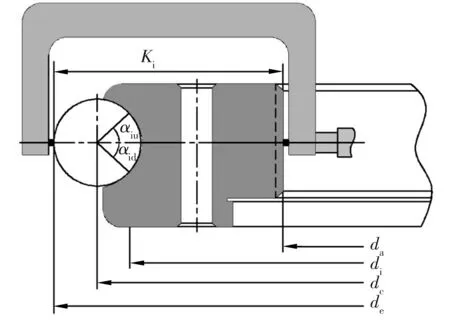
图4 夹球壁厚测量
为了更进一步明确沟道形状对于游隙的影响程度,设计2种游隙配置方案研究沟道形状对于游隙的影响。
2.1 试验方案
为研究沟道形状对负游隙的影响程度,设计对比试验研究不同游隙配制方案下的启动摩擦力矩差异。
方案1:选取一套178991KM(外形尺寸Φ645.897 mm×Φ457.2 mm×79.375 mm,钢球直径Φ31.75 mm)四点接触球转盘轴承的内、外圈,通过更换10组不同钢球直径规值以获得不同的游隙值,进而测量相应的启动摩擦力矩。由于此方案中所使用的内、外套圈为同一组套圈,因而沟道形状对于游隙的影响可以剔除,能够直接反映出无沟道形状参数影响时游隙变化与启动力矩变化之间的关系。
方案2:选取样本数量为20的178991KM四点接触球转盘轴承。测量该批轴承标定位置的沟径尺寸,通过理论计算沟底径尺寸(由于四点接触球轴承沟底存在避免应力集中以及储油作用的圆弧,因而无法直接测量其沟底径)以及不考虑沟道形状影响下的接触点位置尺寸,从而计算出游隙值。测量此20套轴承的启动力矩,研究启动力矩与计算游隙值的关系,从而确定沟道形状对于实际游隙的影响。
2.2 试验结果
图5a为方案1中以10种不同规值的钢球与同一组套圈合套后获得不同的游隙值测试启动摩擦力矩的结果。图中曲线表明,游隙值较大的配置中启动力矩变化不大;游隙值为5 μm的点是启动摩擦力矩变化曲线的重要拐点,游隙值小于5 μm时,随游隙值的减小,对应的启动摩擦力矩整体呈现明显的非线性上升趋势。图中横坐标游隙值的大小采用测夹球壁厚的方法间接计算得到,由于前述测量方法的局限性,横坐标所标注的游隙值不一定准确,这是拐点出现在游隙值为5 μm而不是零点的原因。但启动力矩随游隙变化的趋向性可以很清晰地说明游隙与启动力矩之间的关系。
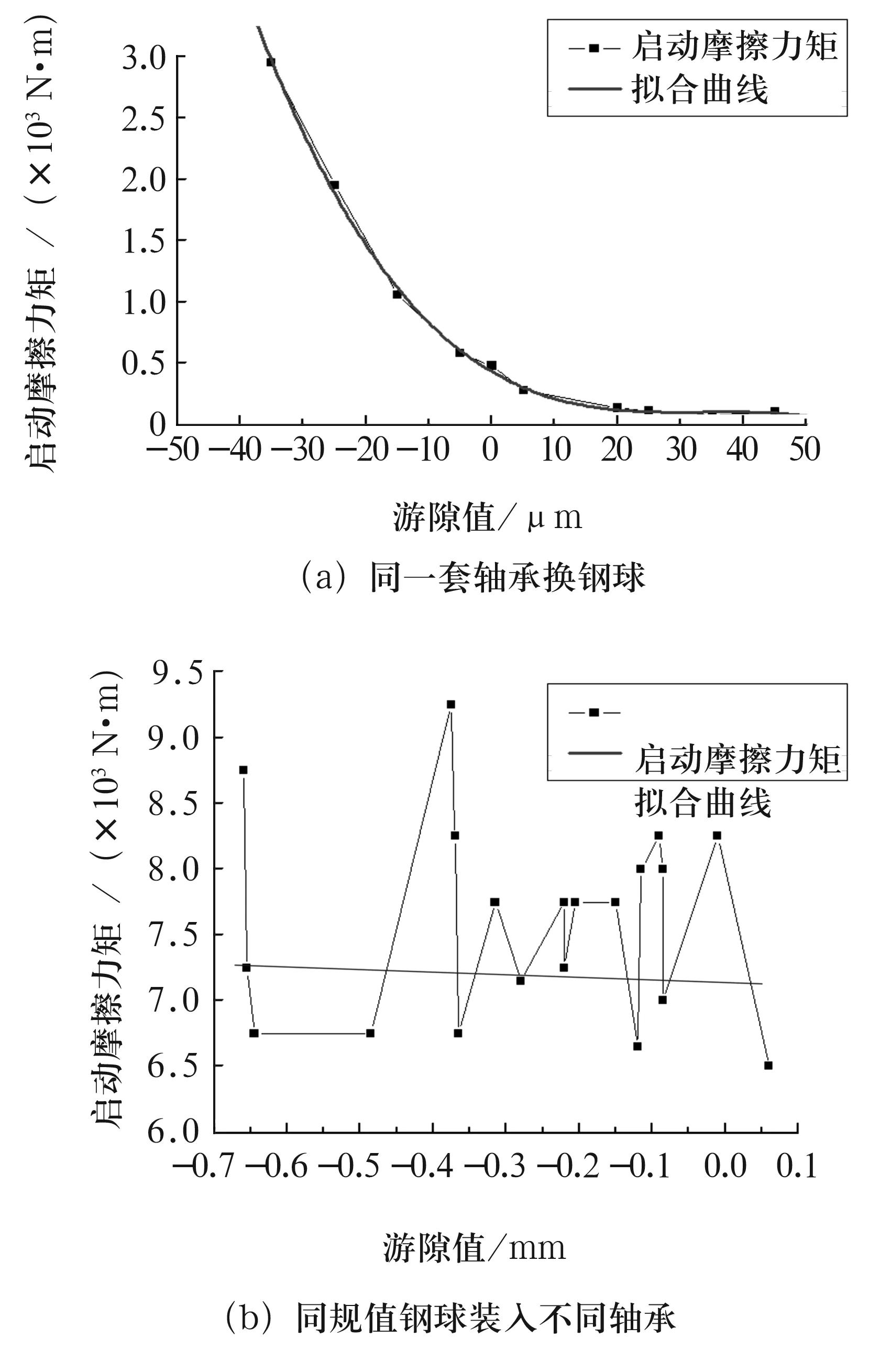
图5 游隙值与启动摩擦力矩的关系
方案2中以同一规值的钢球合套20套178991KM轴承,由于沟道尺寸差异而获得不同的游隙值,测试的游隙与启动摩擦力矩关系如图5b所示。由于圆形偏差对于启动力矩的影响较为明显,游隙计算中综合考虑了圆形偏差对于游隙值的影响并剔除。总体趋势上来说随着游隙减小,启动摩擦力矩存在增加的趋势,但与图5a的递减趋势相比,显然横坐标所标记的游隙变化量并非真实游隙变化量,整体曲线中波动性非常明显,并且存在多个异常变化点。由此可判断计算的游隙值与实际游隙值之间存在较大差异。计算游隙值中唯一大于零的点的启动力矩小于其他19组的启动力矩,因而可判断出其他19套轴承均已带预紧,为负游隙。影响到游隙计算的关键因素中,沟径与圆形偏差因素已经剔除,影响游隙值最为直接的因素即为沟道形状。
依据以上分析,进一步测量合套的20套轴承的内、外圈沟道弦长,以理论计算尺寸为基准值,大于弦长计算值的偏差取为正值、小于弦长计算值的偏差取为负值,每套轴承的内、外圈圆周方向上各取6个点,共计12个点的弦长偏差的均值如图6a所示。对比图6a与图5b,两者图形变换趋势正好相反,弦长偏差为正值时(即沟道形状“张开”),启动摩擦力矩小,可判断出此时游隙的绝对值小,在19套带预紧的负游隙轴承中,弦长偏差越大则启动摩擦力矩往下波动越显著;反之,当弦长偏差为负值时(即沟道形状“收缩”),启动摩擦力矩小,可判断出此时游隙的绝对值大,在19套带预紧的负游隙轴承中,弦长偏差越小则启动摩擦力矩往上波动越显著。
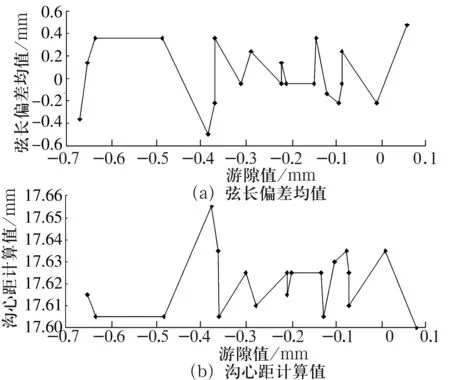
图6 20套轴承的弦长偏差与沟心距
依据径向偏差的均值进一步绘制出沟道形状,可计算出内外圈上、下沟道之间的沟心距如图6b所示。图6b的计算值与(5)式之间有较好的一致性。
3 结束语
四点接触球转盘轴承的沟道形状对转盘轴承的游隙值影响显著,对于游隙大于零的转盘轴承来说,沟道形状主要影响其接触角,进而影响到载荷分布状态;而对于游隙小于零的转盘轴承,沟道形状直接影响游隙值的大小,进而影响到启动力矩。
因此,对于一些有启动力矩指标要求的工况条件,由于沟道形状对负游隙的显著影响,不适宜采用切入磨工艺方法形成沟道,而适宜采用数控硬车的方法来加工沟道。
